xyZGHio

樱花同载酒，终似少年游

0%

浅谈密码学之加密算法

发表于 阅读数： 评论数：
本文字数： 3k 阅读时长 ≈ 6 分钟

本文介绍日常开发中常用的密码学算法

abstract.png

古典密码学

古典密码通常使用替换（将明文中的字母替换为其他字母）、置换（将明文中的字母重新排序，改变排列位置）等简单手段，不需要复杂的机器或算法。故安全性不足，容易破解

  • Caesar Cipher凯撒密码：根据字母表顺序，将明文字母按固定数目偏移后替换为相应的字母进行加密。该加密方式，密钥空间很小，容易被暴力破解
  • Simple Substitution Cipher简单替换密码：根据某种固定的一对一的映射关系，将明文字母替换为另一个字母进行加密。该加密方式，由于映射关系是固定的、一对一的。会导致明文中字母的使用频率与密文中字母的使用频率是一致的，故当密文长度足够长时，可通过频率分析破解

现代密码学

对称加密

所谓对称加密指的是加密、解密使用的都是同一个密钥。由于加密和解密过程相同，故对称加密算法通常计算效率高，适合于大量数据的加解密场景

DES算法

DES（Data Encryption Standard，数据加密标准）算法作为一种采用Feistel网络的对称加密算法。其属于Block Cipher分组密码，分组长度为64位。虽然DES密钥长度为64位，但由于每个字节的第8位是奇偶校验位，故实际上有效的密钥长度只有56位。由于DES算法的密钥较短，目前已不再安全，可通过暴力攻击破解

3DES（Tiple Data Encryption Standard，三重DES）是一种将DES算法重复3次的加密算法。具体加密过程：

  1. 第一次加密：使用密钥1对明文进行DES加密操作
  2. 第二次加密：使用密钥2对Setup 1的结果进行解密操作
  3. 第三次加密：使用密钥3对Setup 2的结果进行加密操作

之所以在3DES算法第二次加密时使用解密操作，是为了保证对DES的向下兼容。因为当密钥1、密钥2、密钥3全部为相同密钥时，3DES即会退化为DES算法。此外，当密钥1、密钥3是相同的密钥，而密钥2使用不同的密钥时，该三重DES称为DES-EDE2；当密钥1、密钥2、密钥3全部为不同密钥时，该三重DES称为DES-EDE3。其中，EDE指的是Encryption加密、Decryption解密、Encryption加密的加密流程

AES算法

AES（高级加密标准，Advanced Encryption Standard）算法同样是一种采用对称加密的加密算法，作为Block Cipher分组密码，其分组长度固定为128位，但其密钥支持128位、192位、256位三种长度。该算法具有良好的安全性，推荐使用

非对称加密

非对称加密中，密钥分为加密密钥、解密密钥两种。其中，加密时使用加密密钥，解密则需要解密密钥。通常，加密密钥是可以任意公开的，以供消息的发送者对明文进行加密，故又被称为Public Key公钥；相对地，解密密钥是绝对不可以公开的，只能有消息的接收者自己持有，故又被称为Private Key私钥。公钥和私钥是一一对应的，因为由某个公钥加密的密文，必须使用与该公钥对应的私钥才能解密，故一对公钥和私钥被称之为Key Pair密钥对。非对称加密算法虽然解决了密钥配送的问题。但相比较于对称加密算法，其速度较慢。同时其存在被中间人攻击的风险

RSA算法

基本原理

RSA算法，作为非对称加密的典型代表。作为目前主流的非对称加密算法，推荐使用。其PlainText明文、Ciphertext密文、密钥都是数字。加密过程可以使用下述公式表示。即，先对明文求e次幂，然后对该结果按N取模，得到的结果即是密文。这里e、N两个数字就组成了公钥，记作(N，e)

解密过程可以使用下述公式表示。即，先对密文求d次幂，然后对该结果按N取模，得到的结果即是明文。这里d、N两个数字就组成了私钥，通常记作(N，d)

RSA算法在产生公钥、私钥的基本步骤如下：

  1. 选择两个大素数：利用伪随机数生成器选择两个足够大的且不相同的随机素数p、q。且p、q越大，加密的安全性越高
  2. 计算N：N=pxq
  3. 计算欧拉函数𝜑(N)。由于N为两个素数的乘积，故可以利用下述公式快速计算
  4. 计算e值：选择一个整数e，要求满足 1<e<𝜑(N) 且 与𝜑(N)互质 即可
  5. 计算d值：找到另一个整数d，使得 (d×e) mod 𝜑(N) = 1

私钥/公钥的选择问题

由于RSA算法的特性，生成的密钥对key1、key2是对等的，本质上是因为e值、d值是对等的。换言之，使用密钥key1加密的密文可以使用密钥key2进行解密，使用密钥key2加密的密文也可以使用密钥key1进行解密。那问题来了，既然生成的两个密钥是对等的。我们是不是可以任意从中选择一个密钥将其对外公开作为公钥，而将另外一个密钥保密作为私钥来使用呢？

从理论上来说，是可以的。但从实际看，是不可以的

  • 首先，我们在使用工具生成RSA密钥时，会发现通常私钥的长度明显比公钥长很多。原因就在于大多数工具生成RSA密钥时，标记为私钥会包含密钥生成过程中的一些原始信息。显然如果选择将该私钥对外公开的，会极大增加公钥被推测破解的风险。安全性大大降低
  • 其次，就算退一万步而言，某个工具生成的私钥不包含原始信息了，也是不可以公开的。讲道理，在生成RSA密钥时计算e值的过程中，e值应该是随机选取的。但实际工程上出于提高加密计算效率的考虑，e值通常会固定取3、65537等较小的值。由于e值较小，故如果我们将(N,e)作为私钥，会大大增加被暴力破解的风险。而RSA算法的实现一般会保证d值很大，故选择(N,d)作为私钥会更安全

ECC算法

ECC算法（椭圆曲线加密算法），一种基于椭圆曲线离散对数问题的非对称加密算法。该算法相比较RSA算法而言，能够以较短长度的密钥提供极高的安全性。故其在计算、传输方面的效率会更高，非常适合嵌入式设备、移动设备等。推荐使用

ElGamal算法

一种基于离散对数问题的非对称加密算法，可用于数据加密、数字签名等场景

混合加密系统

非对称加密算法的公钥由于可以任意公开，从而解决了对称加密算法的密钥配送问题。但其缺点也是存在的，即非对称加密算法的速度远低于对称加密算法。故通常可以将非对称加密算法、对称加密算法组合起来使用，充分利用二者各自的优势。即所谓的混合加密系统。具体地加密过程如下：

  1. 消息发送方生成一个随机的密钥，然后使用该密钥通过对称加密算法来加密消息，得到 消息密文
  2. 消息发送方再利用消息接收方的公钥通过非对称加密算法来加密步骤1中所生成的密钥，得到 对称加密算法的密钥的密文
  3. 将 对称加密算法的密钥的密文、消息密文 二者进行组合后，得到 最终的密文

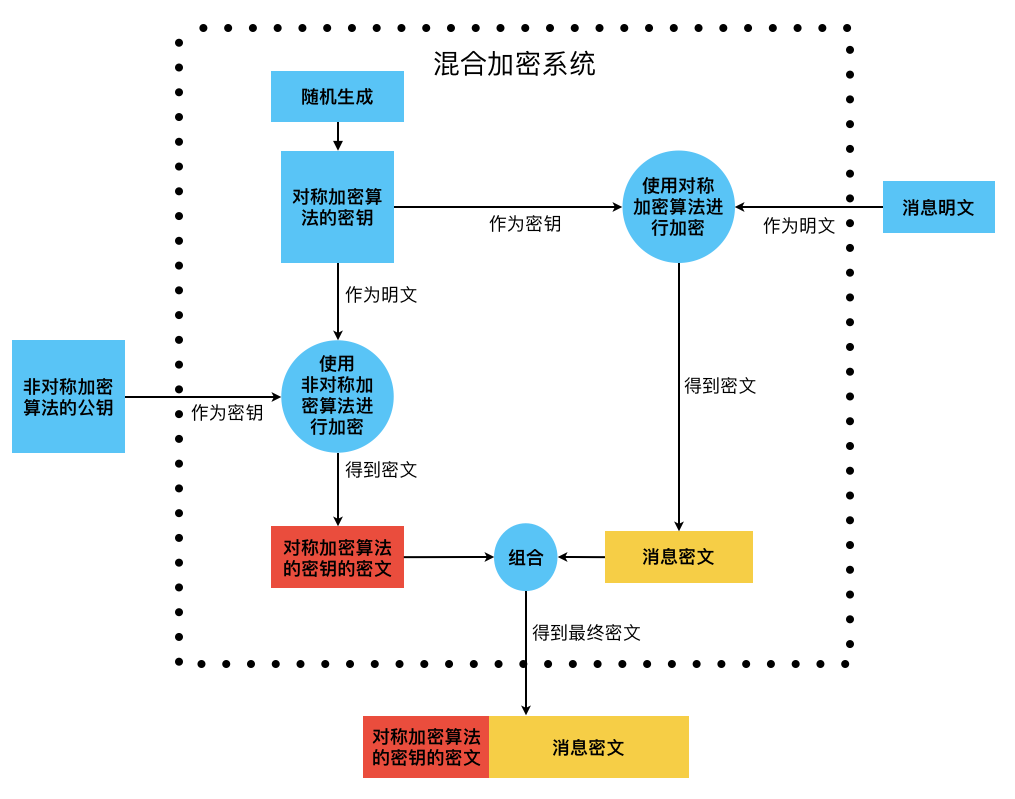
figure 1.png

至于解密也很简单

  1. 消息接收方在收到报文后，按照双方提前约定好的报文格式先将密文进行分离。得到 对称加密算法的密钥的密文、消息密文
  2. 消息接收方利用自己的私钥，将 对称加密算法的密钥的密文 通过非对称加密算法来解密，得到 消息发送方随机生成的对称加密算法的密钥
  3. 消息接收方利用步骤2中得到的对称加密算法的密钥，将 消息密文 通过对称加密算法来解密，最终得到消息明文

参考文献

  1. 图解密码技术·第3版 [日]结城浩著
请我喝杯咖啡捏～

欢迎关注我的微信公众号：青灯抽丝