xyZGHio

樱花同载酒，终似少年游

0%

机器学习之聚类算法：DBSCAN算法

发表于 阅读数： 评论数：
本文字数： 7k 阅读时长 ≈ 14 分钟

这里介绍机器学习中用于聚类的DBSCAN算法

abstract.png

基本原理

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法是一种基于密度的无监督学习的聚类算法。其可将数据集根据分布的密度划分为若干个簇。该算法有两个模型参数：

  • 邻域半径 ϵ：以样本为中心的搜索半径
  • 最小点数 MinPts：如果将某样本视为核心点，则在以该样本为中心、半径为ε的搜索范围内样本数(含该样本自身)的最小阈值

这里先介绍下该算法的核心概念：

  • ϵ-邻域：对于某个样本p而言，在以样本p为中心、ε为半径的范围内的子样本集合。显然样本p的ϵ-邻域包含自身，因为距离为0
  • 核心点：对于某个样本p而言，在以样本p为中心、ε为半径的范围内包含至少MinPts个样本（含样本p自身）。换言之，如果 样本p的ϵ-邻域中的样本数 >= MinPts，则样本p即为核心点
  • 边界点：对于某个样本而言，虽然其不是核心点，但其在某个核心点的ϵ-邻域内
  • 噪声点：对于某个样本而言，其既不是核心点，也不在任何核心点的ϵ-邻域内
  • 密度直达：样本p是一个核心点，且样本q在样本p的ϵ-邻域内，则称：样本q由样本p密度直达
  • 密度可达：对于样本序列p(1),p(2),p(3),…,p(n)而言，若对于任意i(1≤i<n)，都有：样本p(i+1)由样本p(i)密度直达。则称：样本p(n)由样本p(1)密度可达。显然这里的p(1),p(2),p(3),…,p(n-1)样本都必须是核心点，而p(n)样本则可以是 边界点 或 核心点

DBSCAN算法的本质就是先找出数据集中的所有核心点，然后将所有密度可达的样本划分为一个簇。具体流程如下：

  1. 对数据集中的每个样本计算ϵ-邻域。若ϵ-邻域中的样本数满足MinPts最小点数的要求，则该样本标记为核心点。其中，距离的度量方式可根据实际需求选择欧式距离、曼哈顿距离 或 余弦距离等
  2. 将数据集中的所有样本全部标记为未访问
  3. 随机挑选一个未访问的核心点T
    A. 将该核心点T加入到空集合S中。同时，该核心点T标记为已访问
    B. 从集合S中随机取出一个样本。如果该样本为核心点，则将其ϵ-邻域中未访问的样本全部加入到集合S中。相应的，将这些加入到集合S中的样本全部标记已访问
    C. 重复步骤B，直到集合S为空。显然，步骤A～步骤C过程中访问的所有样本都可以由样本T密度可达。故，将这些样本全部划分到一个簇当中即可。至此，该簇就确定了
  4. 重复步骤3，进行下一个簇的划分，直到所有核心点全部被访问后停止
  5. 将数据集中未被任何簇包含的样本标记为噪声点。噪声点的簇编号通常用-1表示

从上述流程不难看出，如果某个边界点在多个核心点的ϵ-邻域内，则其会被分配到第一个处理该边界点的核心点所在的簇中。换言之，该边界点的归属是由核心点的遍历顺序决定的，而这种顺序的依赖性可能会导致聚类结果的不稳定

实践

基于Python的实现

这里基于NumPy提供DBSCAN算法的Python实现，更好的诠释该算法的过程、细节、原理。不过，这里对领域的计算做了一定的优化。并不是一开始就计算所有点的领域，而是按需计算。在一定程度上减少了领域的计算量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
import numpy as np
import matplotlib.pyplot as plt
from collections import deque

def dbscan_cluster(data, eps, min_pts) :
    """
    DBSCAN聚类
    """
    # 样本数 n
    n = data.shape[0]
    # 聚类结果, 所有点的簇编号全部初始化为-1
    cluster_res = np.full(n, -1)
    # 簇编号
    cluster_id = 0

    def region_query(point_index):
        """
        查询指定点的邻域内的所有点
        index: 指定点的索引
        """ 
        nonlocal data, eps
        # 计算该点到所有点的欧式距离。即: 向量差的L2范数
        distances = np.linalg.norm( data[point_index] - data, axis=1 )
        # 领域内所有点的索引
        neighbors_index = np.where(distances<=eps)[0].tolist()
        return neighbors_index

    def expand_cluster(neighbors_index):
        """
        拓展当前簇
        neighbors_index: 领域内所有点的索引
        """
        nonlocal data, eps, min_pts
        nonlocal cluster_res, cluster_id

        queue = deque(neighbors_index)
        while queue:
            cur_index = queue.popleft()
            if cluster_res[cur_index] != -1:
                # 当前点已被分配到某个簇
                continue
                # Note: 这里不会遗漏掉某些核心点的邻域 !!
                #   因为，如果这个点是核心点的话，则在之前的某次循环中
                #   对该点分配簇编号后，立即将其领域的所有点全部加入到队列中
            
            # 将当前点分配到该簇
            cluster_res[cur_index] = cluster_id

            # 计算当前点的领域
            new_neighbors_index = region_query(cur_index)
            # 如果其为核心点，则将其领域内的所有点全部加入队列
            if len(new_neighbors_index) >= min_pts:
                queue.extend(new_neighbors_index)

    # 遍历所有样本
    for i in range(n):
        if cluster_res[i] != -1:
            # 该点已被分配到某个簇
            continue
        
        # 计算当前点的领域
        neighbors_index = region_query(i)
        # 如果其为核心点, 则拓展该簇
        if len(neighbors_index) >= min_pts:
            expand_cluster(neighbors_index)
            # 该簇完全确定，簇编号加1，准备处理下一个簇
            cluster_id += 1 

    return cluster_res

def generate_arc(radius, num, theta_range=[0, 2*np.pi],center_xy=[0,0], noise=[0,0]):
    """
    生成一个圆弧形的点集
    radius: 半径
    num: 点的数量
    theta_range: 角度范围
    center_xy: 圆弧中心点坐标
    noise: 径向噪声的均值、标准差 
    """
    start_theta, end_theta = theta_range
    theta = np.linspace(start_theta, end_theta, num)

    x_0, y_0 = center_xy
    noise_mean, noise_std = noise
    x = x_0 + radius * np.cos(theta) + np.random.normal(noise_mean, noise_std, (num,))
    y = y_0 + radius * np.sin(theta) + np.random.normal(noise_mean, noise_std, (num,))
    return np.vstack((x, y)).T


def load_data():
    """
    构造测试数据
    """
    # 固定种子，为了可重复
    np.random.seed(996)
    circle = generate_arc(radius=20, num=300, noise=[0,1])
    arc1 = generate_arc(radius=5, num=20, theta_range=[0.3*np.pi, 1.7*np.pi], center_xy=[-2.5,-5], noise=[0,0.2])
    arc2 = generate_arc(radius=5, num=20, theta_range=[1.5*np.pi, 2.2*np.pi], center_xy=[0,0], noise=[0,0.2])
    # 噪声数据
    noise_data = np.array([[-4,7],[6,7],[-16,25],[-14,-24],[28,-14]])

    data = np.vstack( (circle, arc1, arc2, noise_data) )
    return data


def plot(data, cluster_res):
    """
    可视化
    """
    # 样本是边缘色为黑色的、o形的点
    scatter = plt.scatter(data[:,0], data[:,1], c=cluster_res, cmap='Accent', marker='o',s=40, edgecolor='k')

    # 聚类结果编号 去重
    cluster_res_set = np.unique(cluster_res)
    # 定义聚类结果的图例说明
    cluster_legend = [f'Cluster #{cluster_label}' if cluster_label != -1 else 'Noise' for cluster_label in cluster_res_set]
    # 获取散点图的颜色句柄
    handles, _ = scatter.legend_elements()  
    # 添加图例
    plt.legend(handles=handles, labels=cluster_legend)

    # 添加标题、轴标签
    plt.title('Custom DBSCAN Cluster')
    plt.xlabel('X Axis')
    plt.ylabel('Y Axis')
    # 显示网格线
    plt.grid(True)
    # X、Y轴比例相等
    plt.axis("equal")
    # 显示图形
    plt.show()


if __name__ == "__main__":
    # 加载测试数据
    data = load_data()
    # 设置模型参数
    eps = 3
    min_pts = 4
    # 聚类
    cluster_res = dbscan_cluster(data, eps, min_pts)
    # 获取聚类结果
    plot(data, cluster_res)

聚类效果如下所示

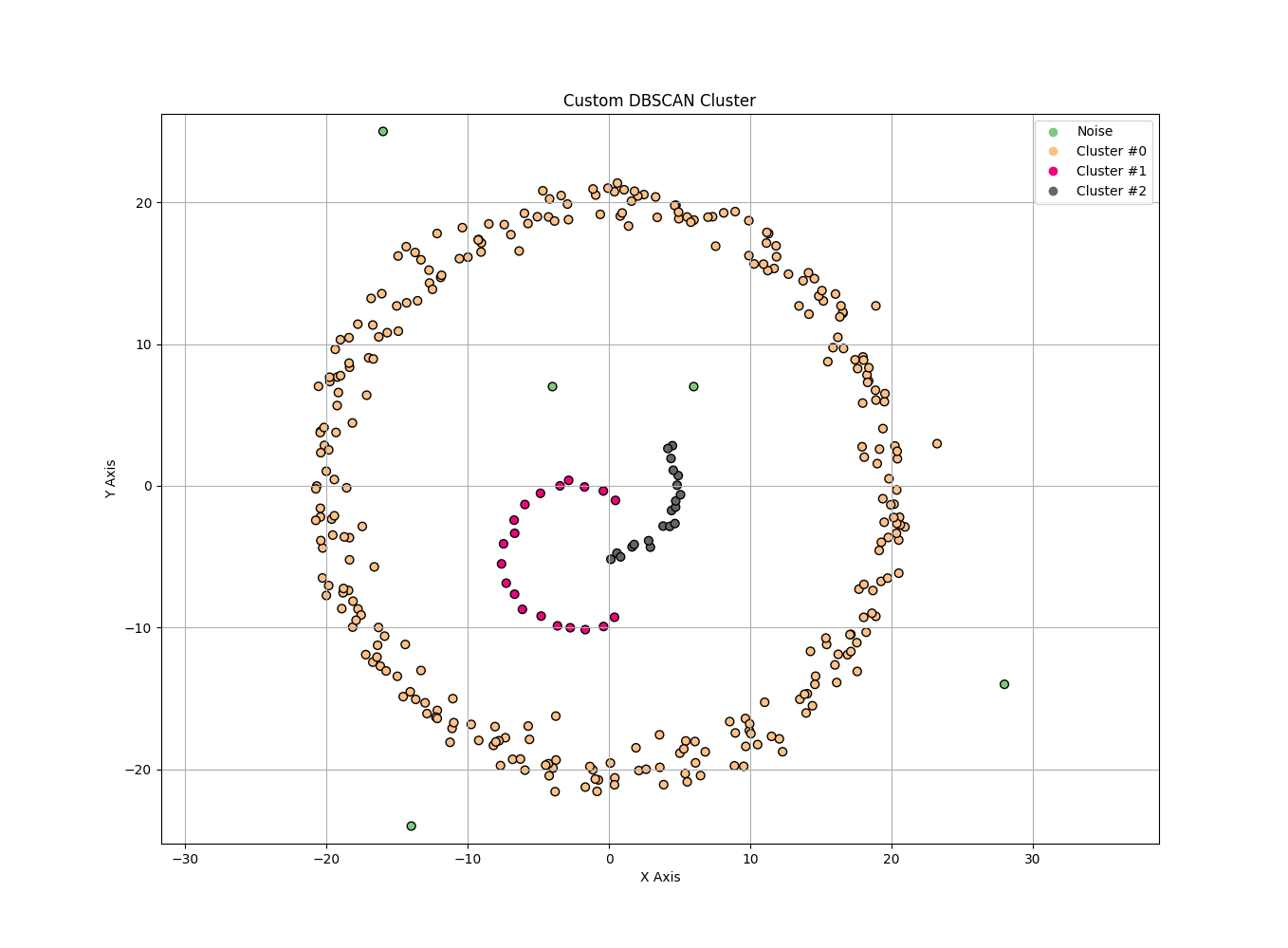
figure 1.png

基于SKlearn的使用

实际开发中可直接使用SKlearn提供的DBSCAN算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN


def generate_arc(radius, num, theta_range=[0, 2*np.pi],center_xy=[0,0], noise=[0,0]):
    """
    生成一个圆弧形的点集
    radius: 半径
    num: 点的数量
    theta_range: 角度范围
    center_xy: 圆弧中心点坐标
    noise: 径向噪声的均值、标准差 
    """
    start_theta, end_theta = theta_range
    theta = np.linspace(start_theta, end_theta, num)

    x_0, y_0 = center_xy
    noise_mean, noise_std = noise
    x = x_0 + radius * np.cos(theta) + np.random.normal(noise_mean, noise_std, (num,))
    y = y_0 + radius * np.sin(theta) + np.random.normal(noise_mean, noise_std, (num,))
    return np.vstack((x, y)).T


def load_data():
    """
    构造测试数据
    """
    # 固定种子，为了可重复
    np.random.seed(996)
    circle = generate_arc(radius=20, num=300, noise=[0,1])
    arc1 = generate_arc(radius=5, num=20, theta_range=[0.3*np.pi, 1.7*np.pi], center_xy=[-2.5,-5], noise=[0,0.2])
    arc2 = generate_arc(radius=5, num=20, theta_range=[1.5*np.pi, 2.2*np.pi], center_xy=[0,0], noise=[0,0.2])
    # 噪声数据
    noise_data = np.array([[-4,7],[6,7],[-16,25],[-14,-24],[28,-14]])

    data = np.vstack( (circle, arc1, arc2, noise_data) )
    return data


def plot(data, cluster_res):
    """
    可视化
    """
    # 样本是边缘色为黑色的、o形的点
    scatter = plt.scatter(data[:,0], data[:,1], c=cluster_res, cmap='Accent', marker='o',s=40, edgecolor='k')

    # 聚类结果编号 去重
    cluster_res_set = np.unique(cluster_res)
    # 定义聚类结果的图例说明
    cluster_legend = [f'Cluster #{cluster_label}' if cluster_label != -1 else 'Noise' for cluster_label in cluster_res_set]
    # 获取散点图的颜色句柄
    handles, _ = scatter.legend_elements()  
    # 添加图例
    plt.legend(handles=handles, labels=cluster_legend)

    # 添加标题、轴标签
    plt.title('DBSCAN Cluster Using SKlearn')
    plt.xlabel('X Axis')
    plt.ylabel('Y Axis')
    # 显示网格线
    plt.grid(True)
    # X、Y轴比例相等
    plt.axis("equal")
    # 显示图形
    plt.show()


if __name__ == "__main__":
    # 加载测试数据
    data = load_data()
    # 设置模型参数
    eps = 3
    min_pts = 4
    # 创建DBSCAN实例, 距离度量使用欧式距离
    dbscan = DBSCAN(eps=eps, min_samples=min_pts, metric='euclidean')
    # 聚类
    dbscan.fit(data)
    # 获取聚类结果
    cluster_res = dbscan.labels_
    plot(data, cluster_res)

聚类效果如下所示

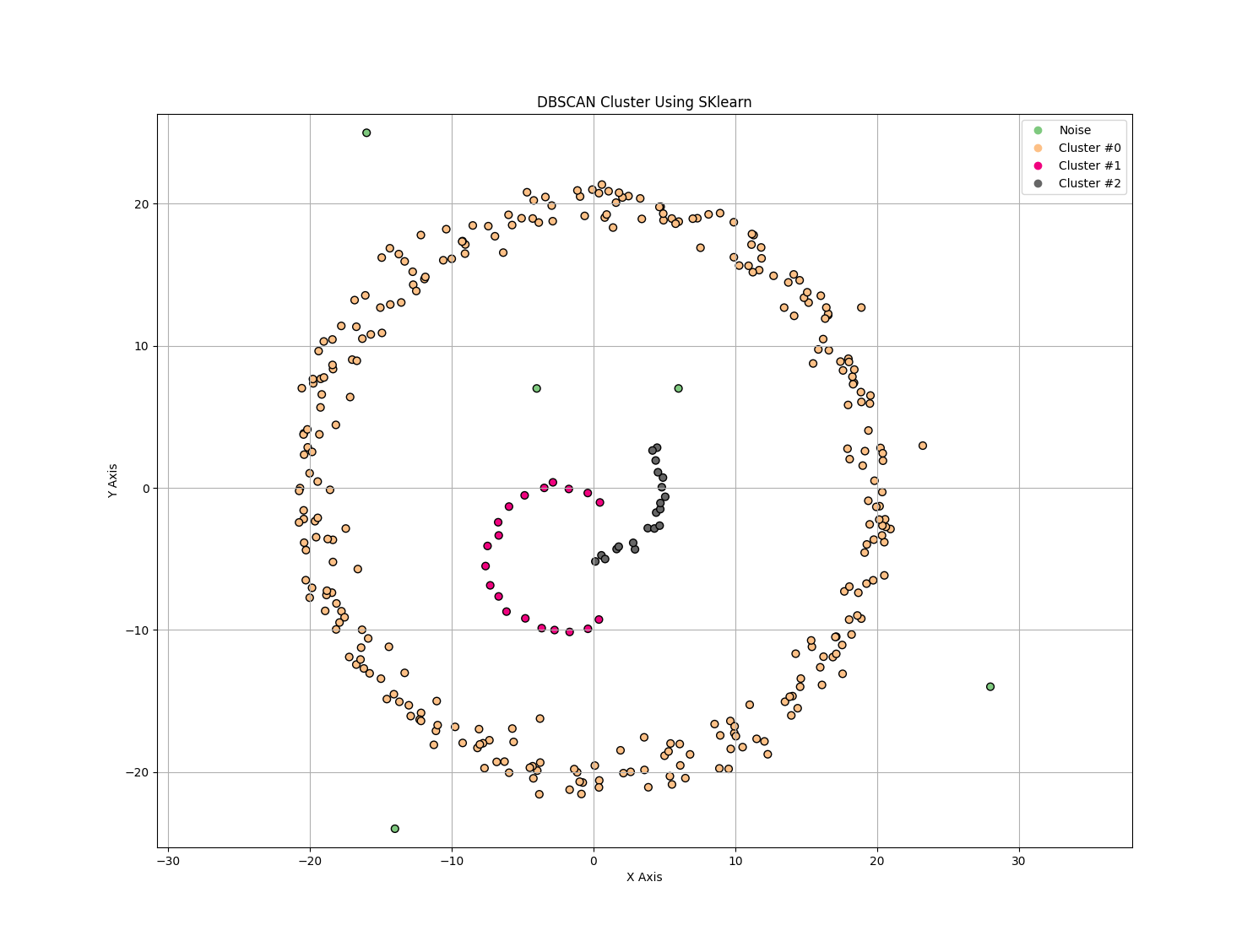
figure 2.png

特点

优点

  • 无监督学习算法，无需训练集
  • 该算法基于密度进行聚类，不依赖于簇的形状。故可适用于任意形状、大小的簇
  • 与K-Means算法不同，DBSCAN算法不需要事先指定簇的数量
  • 对异常值、噪声不敏感，该算法能够自动识别、处理

缺点

  • 数据集较大时，该算法的计算量较大
  • 模型参数ε、MinPts对最终的聚类结果影响很大，不合适的参数甚至会导致聚类错误

参考文献

  • 机器学习 周志华著
  • 机器学习公式详解 谢文睿、秦州著
推荐文章
请我喝杯咖啡捏～
  • 本文作者： Aaron Zhu
  • 本文链接： https://xyzghio.xyz/DBSCAN/
  • 版权声明： 本博客所有文章除特别声明外，均采用 BY-NC-ND 许可协议。转载请注明出处！

欢迎关注我的微信公众号：青灯抽丝