这里介绍机器学习中用于分类的Decision Tree决策树算法

基本原理

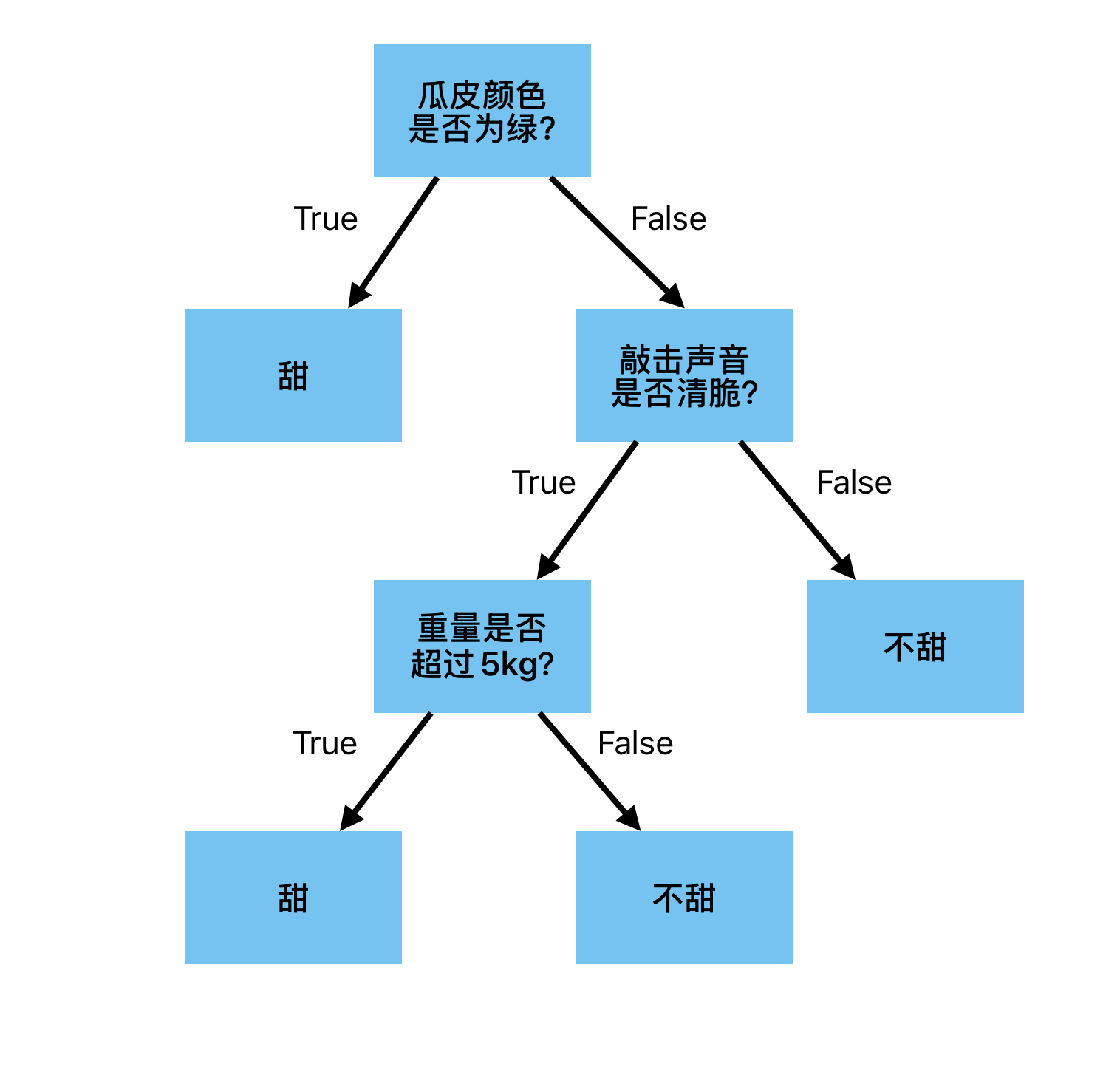
Decision Tree决策树是一种监督学习的分类算法。该模型是一种基于if-else规则的树形结构，包含内部节点、叶子节点。对于内部节点而言，其表达了对某种属性、特征的测试，测试结果决定了下一步的分支流程；而叶子节点则表示最终的分类结果：对于一个训练完成的决策树模型而言，在预测时，从根节点开始不断经过内部节点的属性测试，最终到达叶子节点时结束。此时，该叶子节点表示的分类结果即为该样本的预测分类类别。下图即是一个训练好的决策树，用于判断西瓜甜不甜。至此不难看出，由于本质上该模型就是一堆if-else规则；所以，决策树模型预测结果容易理解、可解释性强

决策树模型的训练是一个递归过程，构建决策树的总体流程如下：

开始：将所有训练样本放到根节点
选择最优特征：从当前节点剩余的特征集合中选择一个最优的特征，作为划分节点的依据
划分节点：根据选择的特征，将当前节点划分为多个子节点。每个子节点对应于该特征的一个测试结果
递归：对每个子节点，重复步骤2~3，直到满足停止条件

常见的停止条件有：

如果当前节点下的所有样本都属于同一个类别，则此时显然无需进行再次划分。可直接将当前节点作为该类别的叶子节点
当前节点下无剩余特征可用于继续划分，其包含下述两种场景。此时，可将当前节点作为叶子节点。其中，类别结果为当前节点的所有样本中样本数最多的类别
- 当前节点的所有样本下已经没有可以继续划分的剩余特征
- 当前节点下所有样本的剩余特征取值都相同。换言之，此时剩余特征没有区分度
当前节点下的样本为空集，显然此时无法继续划分。故将当前节点作为叶子节点，类别结果为父节点的所有样本中样本数最多的类别。此外，也可根据实际业务的偏好，指定为默认的某个类别

决策树的典型缺点是容易过拟合，为此需要引入剪枝。具体地，可分为预剪枝、后剪枝

预剪枝：在树的构建过程中提前停止节点的分裂。防止树过度生长，避免过拟合。常见的策略有：

树的最大深度达到指定阈值
当前节点的样本数小于指定阈值
决策树为CART算法时，当前节点的基尼指数低于指定阈值。因为基尼指数越小，表示其包含的样本不纯度越低、纯度越高。如果节点下所有样本的纯度非常非常高，虽然基尼指数没有达到0，但也没有继续划分的必要，避免过拟合

后剪枝：对已经生成好的决策树进行剪枝。通过某种方法将某个非叶子节点及对应的子树直接替换为叶子节点。这样可实现对决策树泛化能力的提升。常见的后剪枝方法有：

Reduced Error Pruning 错误率降低剪枝（REP）
Pessimistic Error Pruning 悲观错误剪枝（PEP）
Cost Complexity Pruning 代价复杂度剪枝（CCP）

CART算法

对于构建决策树流程中的第2步如何选择最优特征，就需要引入决策树算法。其中，常见的决策树算法有：ID3、C4.5、CART等算法。这里选择CART算法进行介绍。该算法每次选择某个特征进行划分时，会将样本分为两个子集。所以，CART算法生成的决策树实际上是一颗二叉树。其使用Gini Index基尼指数来衡量D样本集的不纯度（纯度指所有样本属于同一类别的程度，不纯度则反之）。该值越小、不纯度越低、纯度越高，说明该样本集中所有样本的类别越具有一致性。具体地：

节点的基尼指数：代表了当前节点中所有样本的不纯度。可通过下述方式计算。其中，D意为该节点下的所有样本；p表示各类别k在样本集D中的比例。从下式也不难看出，该指标可以理解为从数据集中随机抽取两个样本，它们类别不一致的概率

$\text{Gini}(D) = 1 - \sum_{k=1}^{K}p_k^2$

举个例子，如果某个节点下的所有样本类别都是相同的，则该类别的p值是1，其他类别的p值都是0。此时基尼指数为0，不纯度最低，纯度最高

特征划分的基尼指数：用于表示某个特征对样本集的划分效果。值越小，代表按此特征划分后不纯度越低、纯度越高。具体地：首先，根据某个特征A的划分点将当前节点下的样本集D（样本总数记为N）划分到两个子节点当中，则这两个子节点下的样本集分别记为D1、D2（样本总数分别记为N1、N2）；然后，分别计算这两个子节点各自的基尼指数；最后，对这两个基尼指数进行加权平均即可

$\text{Gini}(D,A) = \frac{N_1}{N} \cdot \text{Gini}(D_1) + \frac{N_2}{N} \cdot \text{Gini}(D_2)$

示例

样本集

这里举一个判断消费贷是否审批通过的例子，来说明如何使用CART算法来划分。我们选择的特征有：x1职业类型、x2年收入。训练集样本如下所示

编号	x1 职业类型	x2 年收入	审批结果
#1	全职	5	通过
#2	兼职	2	拒绝
#3	自由职业	18	通过

现在根节点有3个样本。我们使用CART算法来选择最合适的特征来进行划分

离散型特征划分

对于离散型特征而言，由于CART算法生成的是一颗二叉树，故需要穷举所有可能的二元划分方式来寻找最优分割点。故这里对特征x1职业类型的划分方式有3种：
划分方式1：是否为全职？{全职} vs {兼职,自由职业}
划分方式2：是否为兼职？{兼职} vs {全职,自由职业}
划分方式3：是否为自由职业？{自由职业} vs {全职,兼职}

现在我们对上述3种划分方式，依次计算特征划分的基尼指数

划分方式1：是否为全职

左子节点（职业为全职）的样本：#1样本（通过）
左子节点的基尼指数：

$G(left) = 1 - (1^2+0^2) = 0$

右子节点（职业不为全职）的样本：#2样本（拒绝）、#3样本（通过）
右子节点的基尼指数：

$G(right) = 1 - ((\frac{1}{2})^2+(\frac{1}{2})^2) = 0.5$

该划分方式的加权基尼指数：

$G = \frac{1}{3} \cdot 0 + \frac{2}{3} \cdot 0.5 \approx 0.3333333333$

划分方式2：是否为兼职

左子节点（职业为兼职）的样本：#2样本（拒绝）
左子节点的基尼指数：

$G(left) = 1 - (0^2+1^2) = 0$

右子节点（职业不为兼职）的样本：#1样本（通过）、#3样本（通过）
右子节点的基尼指数：

$G(right) = 1 - (1^2+0^2) = 0$

该划分方式的加权基尼指数：

$G = \frac{1}{3} \cdot 0 + \frac{2}{3} \cdot 0 = 0$

划分方式3：是否为自由职业

左子节点（职业为自由职业）的样本：#3样本（通过）
左子节点的基尼指数：

$G(left) = 1 - (1^2+0^2) = 0$

右子节点（职业不为自由职业）的样本：#1样本（通过）、#2样本（拒绝）
右子节点的基尼指数：

$G(right) = 1 - ((\frac{1}{2})^2+(\frac{1}{2})^2) = 0.5$

该划分方式的加权基尼指数：

$G = \frac{1}{3} \cdot 0 + \frac{2}{3} \cdot 0.5 \approx 0.3333333333$

连续型特征划分

对于连续型特征而言，CART算法先会对所有取值进行升序排序：{2, 5, 18}，然后将各相邻值的中间点作为分割点。故这里对特征x2年收入的划分方式，就有下述2种：
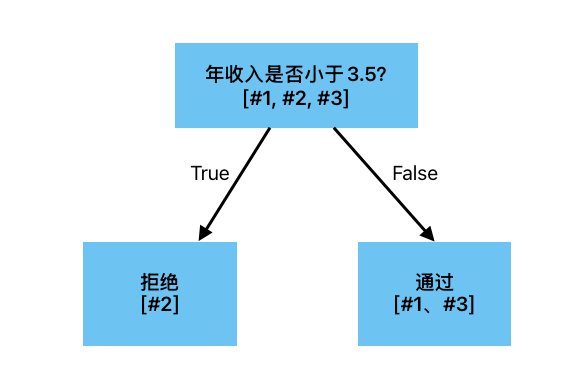
划分方式4：分割点：(2+5)/2 = 3.5，年收入是否小于3.5
划分方式5：分割点：(5+18)/2 = 11.5，年收入是否小于11.5

现在我们对上述2种划分方式，依次计算特征划分的基尼指数

划分方式4：年收入是否小于3.5

左子节点（年收入小于3.5）的样本：#2样本（拒绝）
左子节点的基尼指数：

$G(left) = 1 - (0^2+1^2) = 0$

右子节点（年收入不小于3.5）的样本：#1样本（通过）、#3样本（通过）
右子节点的基尼指数：

$G(right) = 1 - (1^2+0^2) = 0$

该划分方式的加权基尼指数：

$G = \frac{1}{3} \cdot 0 + \frac{2}{3} \cdot 0 = 0$

划分方式5：年收入是否小于11.5

左子节点（年收入小于11.5）的样本：#1样本（通过）、#2样本（拒绝）
左子节点的基尼指数：

$G(left) = 1 - ((\frac{1}{2})^2+(\frac{1}{2})^2) = 0.5$

右子节点（年收入不小于11.5）的样本：#3样本（通过）
右子节点的基尼指数：

$G(right) = 1 - (1^2+0^2) = 0$

该划分方式的加权基尼指数：

$G = \frac{2}{3} \cdot 0.5 + \frac{1}{3} \cdot 0 \approx 0.3333333333$

划分结果

至此可以看出，划分方式2、划分方式4的加权基尼指数都是最小的，均为0。意为按此种方式划分后，左、右子节点的纯度最高。这里我们选择划分方式4（年收入是否小于3.5）来作为根节点的划分条件，不难发现划分后，左、右子节点中的样本类型都属于同一个类别，满足停止条件不再进行划分

实践

下面通过SKlearn提供的Decision Tree决策树分类器来实现一个分类任务，其默认使用CART算法来进行实现。这里选用为经典的鸢尾花Iris数据集。该数据集包含150个样本，选取了鸢尾花的四个特征（sepal length花萼长度、sepal width花萼宽度、petal length花瓣长度、petal width花瓣宽度）用于预测鸢尾花的品种（setosa/versicolor/virginica）

from sklearn import datasets
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
import seaborn as sns
import numpy as np

# 加载数据集: 鸢尾花
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 特征名称
feature_names = iris.feature_names
# 类别名称
label_names = iris.target_names

# 划分训练集、测试集，比例为7:3。固定random_state种子保证每次划分结果一样，可重复
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=69)

# 创建决策树分类器实例,固定random_state保证结果一样可重复
dt = DecisionTreeClassifier(random_state=1314)

# 训练模型
dt.fit(X_train, y_train)

# 预测测试集
y_pred = dt.predict(X_test)

# 计算评估指标
report = classification_report(y_test, y_pred, target_names=label_names)
print("------------------------ 评估指标 ------------------------")
print(f"{report}")

print("------------------------ 特征重要性 ------------------------")
# 获取特征的重要性
importance = dt.feature_importances_
# 特征重要性降序排序的索引
index = np.argsort(importance)[::-1]
for i in index:
    print(f"{feature_names[i]:^21}: {importance[i]:.4f}")

# 计算混淆矩阵
confusion_matrix = confusion_matrix(y_true=y_test,y_pred=y_pred)

# 绘制混淆矩阵
plt.figure("figure 1")
# annot=True: 每个单元格显示数值; fmt="d": 单元格数值格式为整数
# xticklabels / yticklabels: 设置X轴/Y轴的刻度标签名称
sns.heatmap(confusion_matrix, annot=True, cmap="Blues", fmt="d", xticklabels=label_names, yticklabels=label_names)
# X轴标题：预测标签
plt.xlabel("predicted Label")
# Y轴标题：真实标签
plt.ylabel("True Label")
plt.title("Confusion Matrix")

# 可视化 决策树
plt.figure("figure 2", figsize=(20,10))
# 绘制决策树。filled=True: 填充颜色
plot_tree(dt, feature_names=feature_names, class_names=label_names, filled=True)
plt.title("Decision Tree")
plt.show()

输出如下所示

------------------------ 评估指标 ------------------------
              precision    recall  f1-score   support

      setosa       1.00      1.00      1.00        16
  versicolor       0.86      1.00      0.92        12
   virginica       1.00      0.88      0.94        17

    accuracy                           0.96        45
   macro avg       0.95      0.96      0.95        45
weighted avg       0.96      0.96      0.96        45

------------------------ 特征重要性 ------------------------
  petal width (cm)   : 0.9119
  petal length (cm)  : 0.0411
  sepal width (cm)   : 0.0334
  sepal length (cm)  : 0.0135

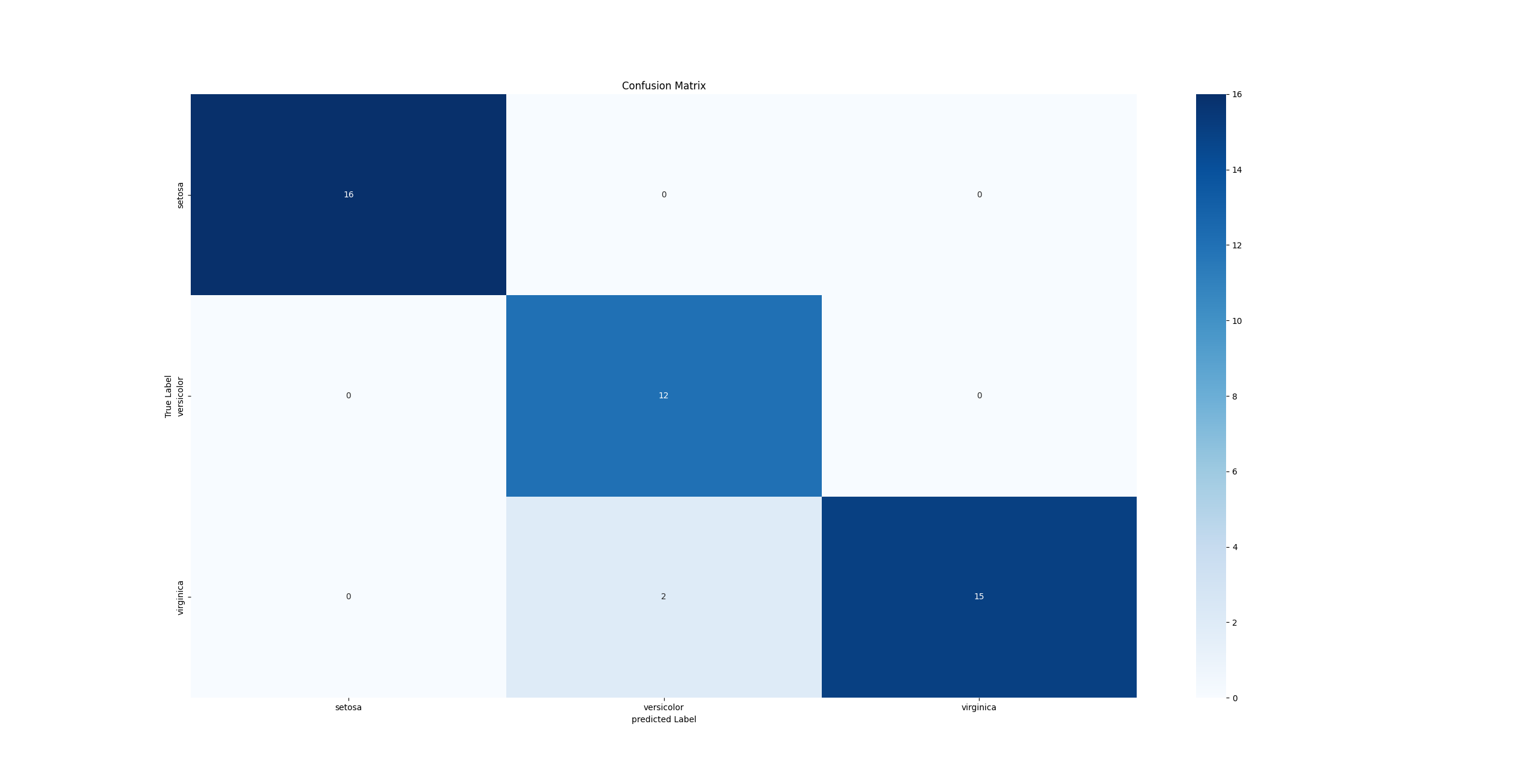
混淆矩阵的结果如下

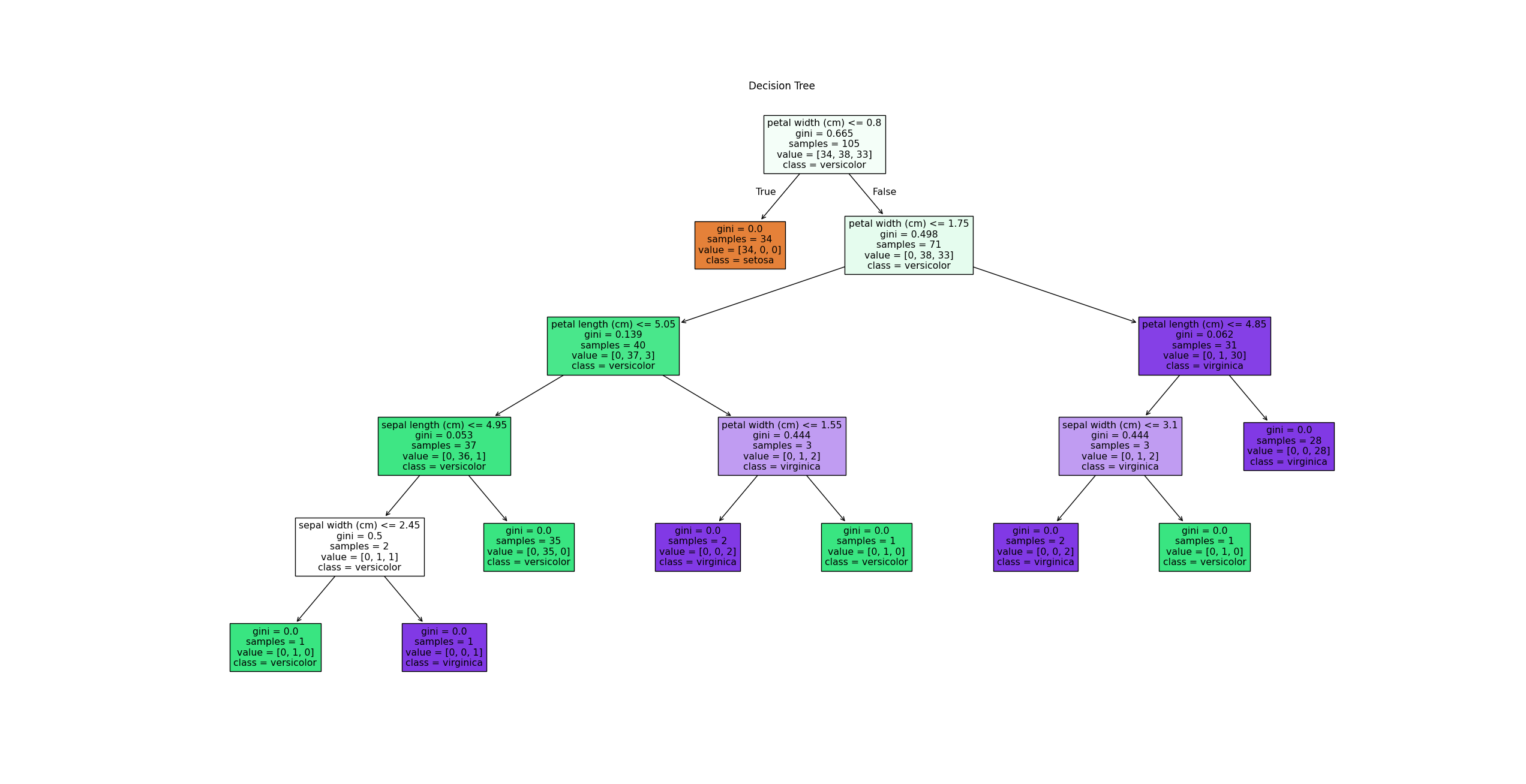
决策树的可视化效果如下所示。这里以根节点为例，解释节点中各信息的含义

petal width(cm)<=0.8：表示该节点采用的属性测试。其中，满足条件的样本将会被分配到左子节点，不满足条件的样本将会被分配到右子节点
gini = 0.665：表示该节点的基尼指数，用于衡量该节点的不纯度
samples=105：表示该节点下的样本数
value =[34,38,33] ：表示该节点下每个类别的样本数量。即：类别索引为0的样本有34个、类别索引为1的样本有38个、类别索引为2的样本有33个
class= versicolor：表示在该节点下，模型预测的最可能的分类结果。即如果在该节点停止的话，模型将预测的类别

特点

优点

直观易懂、可解释性强
支持多分类任务
支持离散型、连续型特征

缺点

容易过拟合

参考文献

机器学习周志华著
机器学习公式详解谢文睿、秦州著
图解机器学习和深度学习入门山口达辉、松田洋之著

xyZGHio

机器学习之分类算法：Decision Tree决策树

基本原理

CART算法

示例

样本集

离散型特征划分

划分方式1：是否为全职

划分方式2：是否为兼职

划分方式3：是否为自由职业

连续型特征划分

划分方式4：年收入是否小于3.5

划分方式5：年收入是否小于11.5

划分结果

实践

特点

优点

缺点

参考文献