xyZGHio

樱花同载酒，终似少年游

0%

GoF设计模式(十五)：Interpreter Pattern 解释器模式

发表于 更新于 分类于 阅读数： 评论数：
本文字数： 7k 阅读时长 ≈ 14 分钟

Interpreter Pattern解释器模式，其是一种在日常开发很少会用到的行为型设计模式

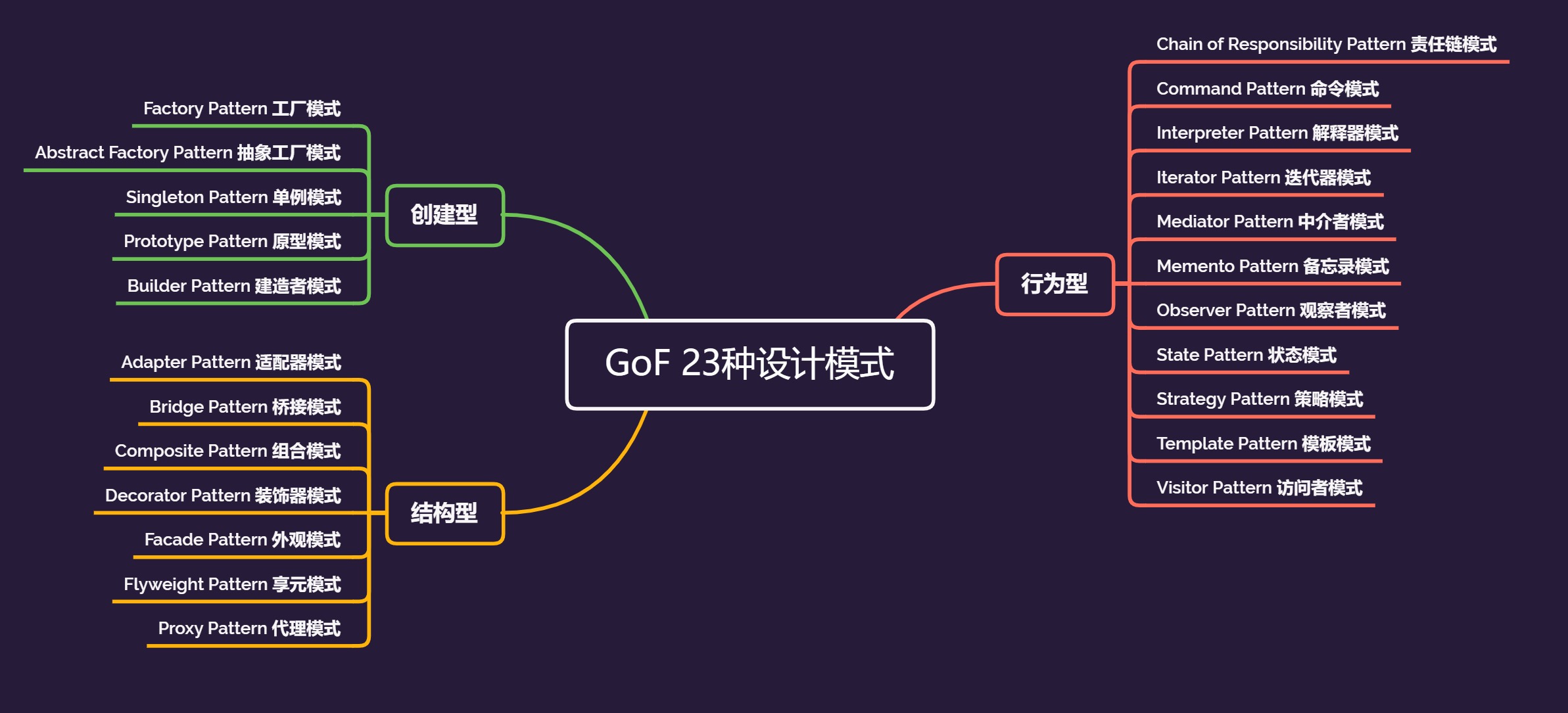
abstract.jpeg

模式思想

有的时候，我们可能需要自己创建一个新的编程语言或表达式，同时针对这个新语言或表达式也会有一些特定的文法规则。这个时候我们就可以通过解释器模式，来解释、执行这个新的语言或表达式。故该模式常见的应用场景：正则表达式、SQL解析、XML解析等等。在本文的例子中，我们将会通过解释器模式来实现四则运算（加、减、乘、除）

在解释器模式中，其有以下几个角色：

  • 抽象表达式：其是一个抽象角色，定义了具体的表达式角色需要实现的interpreter方法，该方法通常被称为解释方法。即本文的Expression接口
  • 非终止符表达式角色：其是抽象表达式的具体实现，其通过实现interpreter方法来描述文法规则。比如对于表达式a+b而言，其中的+加号即是一个非终止符。该符号表示对左右两边的操作数执行相加操作，故在解释器模式下，这个相加的语法规则即可通过一个非终止符表达式角色来表示、实现、解释。具体地在本文中，即是我们的AddOperator加法操作符。类似地还有，SubOperator减法操作符、MulOperator乘法操作符、DivOperator除法操作符类
  • 终止符表达式角色：终结符表达式同样是抽象表达式的实现类。比如对于表达式a+b而言，这里a、b变量即是一个终止符，相应的在本文中可通过终止符表达式角色Variable类来实现。一般地，我们可将变量的值存储在环境角色中。这样变量即通过实现interpreter方法来获取其所代表的数值
  • 环境角色：也被称之为上下文角色。其用于存储在解释的过程中所需的一些全局信息。具体地，即本文的Context上下文类。在本文的例子中，我们通过其来存储变量所代表的值

基于中缀表达式的加、减法

其实仅仅依靠上面的介绍，一般还是很难彻底的理解所谓的解释器模式。所以下面我们来通过具体的例子实现来帮助大家更好的理解。这里，我们先来实现一个基于中缀表达式的支持加法、减法的解释器。所谓中缀表达式，其是一种我们日常见到最多的算术或逻辑公式表示方法。即操作符是以中缀形式处于操作数的中间（例如，3 + 4）

首先，我们定义一个抽象表达式角色，可以看到其只有一个interpreter方法

1
2
3
4
5
6
7
8
9
10
11
/**
 * 抽象表达式角色
 */
public interface Expression {
    /**
     * 解释方法
     * @param context
     * @return
     */
    int interpreter(Context context);
}

然后，我们通过两个具体的非终止符表达式角色——AddOperator、SubOperator类，来实现加法、减法两个文法规则

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/**
 * 非终止符表达式角色：加法操作符
 */
public class AddOperator implements Expression {
    /**
     * 第一个操作数
     */
    private Expression num1;

    /**
     * 第二个操作数
     */
    private Expression num2;

    public AddOperator(Expression num1, Expression num2) {
        this.num1 = num1;
        this.num2 = num2;
    }

    /**
     * 语法规则解释: 加法
     * @param context
     * @return
     */
    @Override
    public int interpreter(Context context) {
        int result = num1.interpreter(context) + num2.interpreter(context);
        return result;
    }
}
...
/**
 * 非终止符表达式角色：减法操作符
 */
public class SubOperator implements Expression {
    /**
     * 第一个操作数
     */
    private Expression num1;

    /**
     * 第二个操作数
     */
    private Expression num2;

    public SubOperator(Expression num1, Expression num2) {
        this.num1 = num1;
        this.num2 = num2;
    }

    /**
     * 语法规则解释: 减法
     * @param context
     * @return
     */
    @Override
    public int interpreter(Context context) {
        int result = num1.interpreter(context) - num2.interpreter(context);
        return result;
    }
}

在本文的例子中，终止符表达式角色只有一个，即我们的计算表达式中的变量。其通过context上下文中来获取变量所代表的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * 终止符表达式角色：变量
 */
public class Variable implements Expression {

    /**
     * 变量名
     */
    private String varName;

    public Variable(String varName) {
        this.varName = varName;
    }

    /**
     * 语法规则解释: 从context上下文中获取变量的值
     * @param context
     * @return
     */
    @Override
    public int interpreter(Context context) {
        return context.getVarValue(varName);
    }
}

最后，为了保存各变量所表示的值。我们直接通过HashMap来实现Context类即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * 上下文角色
 */
public class Context {
    private Map<String, Integer> map = new HashMap<>();

    /**
     * 定义变量的值
     * @param varName
     * @param varValue
     */
    public void define(String varName, Integer varValue) {
        map.put(varName, varValue);
    }

    /**
     * 获取变量的值
     * @param varName
     * @return
     */
    public int getVarValue(String varName) {
        return map.get(varName);
    }
}

现在，就让我们用这个解释器来计算加、减法吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * 基于中缀表达式的加、减法的 Interpreter Pattern 解释器模式Demo
 */
public class Demo1 {
    public static void main(String[] args) {
        // 定义上下文，即定义变量的值
        Context context = new Context();
        context.define("a",3);
        context.define("b",5);
        context.define("c",7);

        Expression a = new Variable("a");
        Expression b = new Variable("b");
        Expression c = new Variable("c");

        System.out.println("------------ Test 1 ------------");
        // 计算表达式 a+b
        Expression aAddb = new AddOperator(a,b);
        Integer result1 = aAddb.interpreter(context);
        System.out.println("a+b = " + result1);

        System.out.println("------------ Test 2 ------------");
        // 计算表达式 a+b-c
        Expression aAddbSubc = new SubOperator( aAddb, c ); // client 客户端负责组装 AST抽象语法树
        Integer result2 = aAddbSubc.interpreter(context);
        System.out.println("a+b-c = " + result2);
    }
}

测试结果如下所示，符合预期

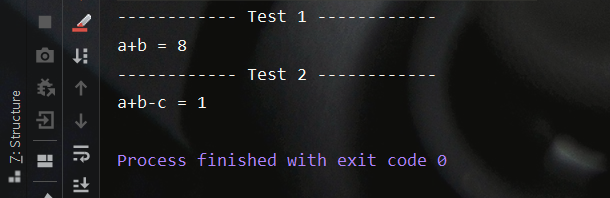
figure 1.png

基于后缀表达式(逆波兰式)的四则运算(加、减、乘、除法)

前面我们介绍了中缀表达式，下面我们来介绍另外两种算术或逻辑公式表示方法

前缀表达式：

又被称作波兰式(PN) ，操作符是以前缀形式处于操作数的前面（例如，+ 3 4）。前缀表达式的计算方法如下：

  1. 从右往左扫描表达式
  2. 遇到数字直接入栈
  3. 遇到运算符，先从栈中弹出两个数作为操作数，然后执行相应的运算，最后将运算的结果压入栈中
  4. 当表达式扫描完毕，则此时栈顶元素即为计算结果

后缀表达式：

又被称作逆波兰式(RPN) ，操作符是以后缀形式处于操作数的后面（例如，3 4 +）。后缀表达式的计算方法如下：

  1. 从左往右扫描表达式
  2. 遇到数字直接入栈
  3. 遇到运算符，先从栈中弹出两个数作为操作数，然后执行相应的运算，最后将运算的结果压入栈中
  4. 当表达式扫描完毕，则此时栈顶元素即为计算结果

在上面的例子中，我们只实现了加、减法这两种文法规则，原因就在于乘、除法的优先级比加、减法高。虽然中缀表达式更符合人类的直觉习惯，但对于计算机来说却并不便于解析、计算。而在前缀、后缀表达式中，一方面其不存在括号，另一方面更重要的是其在计算过程中无需考虑各运算符的优先级，只需顺序计算即可。故非常适合计算机来处理求值。所以这里我们来实现一个基于后缀表达式(逆波兰式)的四则运算(加、减、乘、除法)的解释器模式

由于加、减法的文法规则在上文示例中已经实现过可以直接复用，故这里给出乘、除法的文法规则的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
/**
 * 非终止符表达式角色：乘法操作符
 */
public class MulOperator implements Expression {
    /**
     * 第一个操作数
     */
    private Expression num1;

    /**
     * 第二个操作数
     */
    private Expression num2;

    public MulOperator(Expression num1, Expression num2) {
        this.num1 = num1;
        this.num2 = num2;
    }

    /**
     * 语法规则解释: 乘法
     * @param context
     * @return
     */
    @Override
    public int interpreter(Context context) {
        int result = num1.interpreter(context) * num2.interpreter(context);
        return result;
    }
}
...
/**
 * 非终止符表达式角色：除法操作符
 */
public class DivOperator implements Expression {
    /**
     * 第一个操作数
     */
    private Expression num1;

    /**
     * 第二个操作数
     */
    private Expression num2;

    public DivOperator(Expression num1, Expression num2) {
        this.num1 = num1;
        this.num2 = num2;
    }

    /**
     * 语法规则解释: 除法
     * @param context
     * @return
     */
    @Override
    public int interpreter(Context context) {
        int result = num1.interpreter(context) / num2.interpreter(context);
        return result;
    }
}

值得一提的是，解释器模式并不负责AST抽象语法树的生成构建工作。在上面的例子中大家可以看到，AST抽象语法树是交由client客户端直接组装完成的。这里我们利用后缀表达式的求值计算规则来直接解析表达式并构建AST抽象语法树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
 * AST抽象语法树工具
 */
public class ASTUtil {
    /**
     * 构建AST抽象语法树
     * @param str
     * @return
     */
    public static Expression build(String str) {
        Stack<Expression> stack = new Stack<>();
        // 使用空格作为分隔符进行切分
        String[] strArray = str.split(" ");

        // 按从左到右的顺序依次扫描
        for( String element : strArray ) {
            switch (element) {
                case "+":   // 遇到操作符
                case "-":
                case "*":
                case "/":
                    // 1. 先从栈中弹出两个操作数
                    Expression num1 = stack.pop();  // 获取第一个操作数
                    Expression num2 = stack.pop();  // 获取第二个操作数
                    // 2. 构造结果表达式
                    Expression result = null;
                    switch (element) {
                        case "+":
                            result = new AddOperator(num1, num2);
                            break;
                        case "-":
                            result = new SubOperator(num1, num2);
                            break;
                        case "*":
                            result = new MulOperator(num1, num2);
                            break;
                        case "/":
                            result = new DivOperator(num1, num2);
                            break;
                    }
                    // 3. 将结果压入栈中
                    stack.push(result);
                    break;
                default:    // 遇到操作数
                    // 构造变量表达式, 直接入栈
                    Expression var = new Variable(element);
                    stack.push( var );
            }
        }
        return stack.pop();
    }
}

剩余部分的实现，可以直接复用我们上面那个例子的代码。现在让我们来看看效果如何

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
 * 基于后缀表达式(逆波兰式)的四则运算(加、减、乘、除法)的 Interpreter Pattern 解释器模式Demo
 */
public class Demo2 {
    public static void main(String[] args) {
        // 定义上下文，即定义变量的值
        Context context = new Context();
        context.define("a",8);
        context.define("b",1);
        context.define("c",2);
        context.define("d",4);
        context.define("e",5);

        // 计算中缀表达式 b - a + e * d / c 值，即计算后缀表达式(逆波兰式) a b c d e * / + - 结果
        String str = "a b c d e * / + -";

        // 构建AST抽象语法树
        Expression expression = ASTUtil.build(str);
        Integer result =  expression.interpreter(context);
        System.out.println("期望值: 3 实际值: " + result);
    }
}

测试结果如下，符合预期

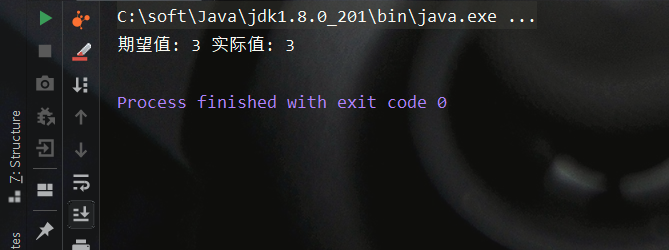
figure 2.png

参考文献

  1. Head First 设计模式 弗里曼著
推荐文章
请我喝杯咖啡捏～

欢迎关注我的微信公众号：青灯抽丝