机器学习之聚类算法：K-Means算法

这里介绍机器学习中用于聚类的K-Means算法

基本原理

该聚类算法可将将数据集划分指定数量的K个簇，其是一种无监督学习的聚类算法。算法流程如下：

1. 初始化K个质心，可从数据集中随机抽取K个样本作为初始质心
2. 对于数据集中的每个样本而言，分别计算其到K个质心的距离（距离度量一般使用欧式距离，其他可用的度量方式有：曼哈顿距离、余弦距离等），然后将该样本归属到距离最近的某质心所对应的簇当中
3. 对于每个簇而言，利用其所属的全部样本，计算平均值作为新的质心
4. 重复第2~3步。迭代的终止条件可以组合选用下述条件
   • 样本的分类结果没有发生任何变化
   • 最大迭代次数
   • SSE(Sum of Squared Errors，误差平方和)小于指定阈值

上述的SSE表达的具体含义是：所有样本到其对应簇的质心的距离的平方和。具体公式如下所示。其中，K是簇的数量；C表示该簇所属的全部样本集合，dist(x,μ)表示样本x到质心μ的距离。注意：计算SSE时使用的距离度量 需与 上述第2步使用的距离度量 保持一致

$$\text{SSE} = \sum_{i=1}^{K} \sum_{x \in C_i} dist(x,\mu_i)^2$$

实践

基于Python的实现

这里基于NumPy提供K-Means算法的Python实现，更好的诠释该算法的过程、细节、原理

import numpy as np
import matplotlib.pyplot as plt

def kmeans_cluster(data, k, max_iters=10000) :
    """
    K-Means聚类
    """
    # 样本数 n
    n = data.shape[0]
    # 聚类结果
    cluster_res = np.zeros(n)

    # K个随机的初始质心
    random_index = np.random.choice(n, k, replace=False)
    centroids = data[random_index]
    for _ in range(max_iters):
        # 遍历所有样本
        for i in range(n):
            sample = data[i]
            # 计算该样本到各质心的欧式距离。即: 向量差的L2范数
            distances = np.linalg.norm(sample-centroids, axis=1)

            # 该样本分配到距离最近的质心
            cluster_res[i] = np.argmin(distances)
        
        # 计算新质心
        new_centroids = np.array(
            [data[np.where(cluster_res==j)].mean(axis=0) for j in range(k)]
        )

        # 质心没有变化
        if np.all(centroids == new_centroids):
            break

        centroids = new_centroids
    return centroids, cluster_res


def load_data():
    """
    构造测试数据
    """
    # 固定种子，为了可重复
    np.random.seed(996)
    data = np.vstack((
        # 生成形状为（80,2）、满足正态分布的随机数
        np.random.randn(80, 2) + np.array([3, 8]),
        np.random.randn(80, 2)*1.5 + np.array([7,-2]),
        np.random.randn(80, 2)*2 + np.array([-6, -3])
    ))
    return data


def plot(data, centroids, cluster_res):
    """
    可视化
    """
    # 样本是边缘色为黑色的、o形的点
    plt.scatter(data[:,0], data[:,1], c=cluster_res, cmap='viridis', marker='o', edgecolor='k')
    # 质心为红色的、方形的点
    plt.scatter(centroids[:,0], centroids[:,1], c='red', marker='s', s=70, label='centroid')
    # 添加标题、轴标签
    plt.title('Custom K-Means Cluster')
    plt.xlabel('X Axis')
    plt.ylabel('Y Axis')
    # 添加图例
    plt.legend()
    # 显示网格线
    plt.grid(True)
    # X、Y轴比例相等
    plt.axis("equal")
    # 显示图形
    plt.show()


if __name__ == "__main__" :
    data = load_data()
    k = 3
    centroids, cluster_res = kmeans_cluster(data, k)
    plot(data, centroids, cluster_res)

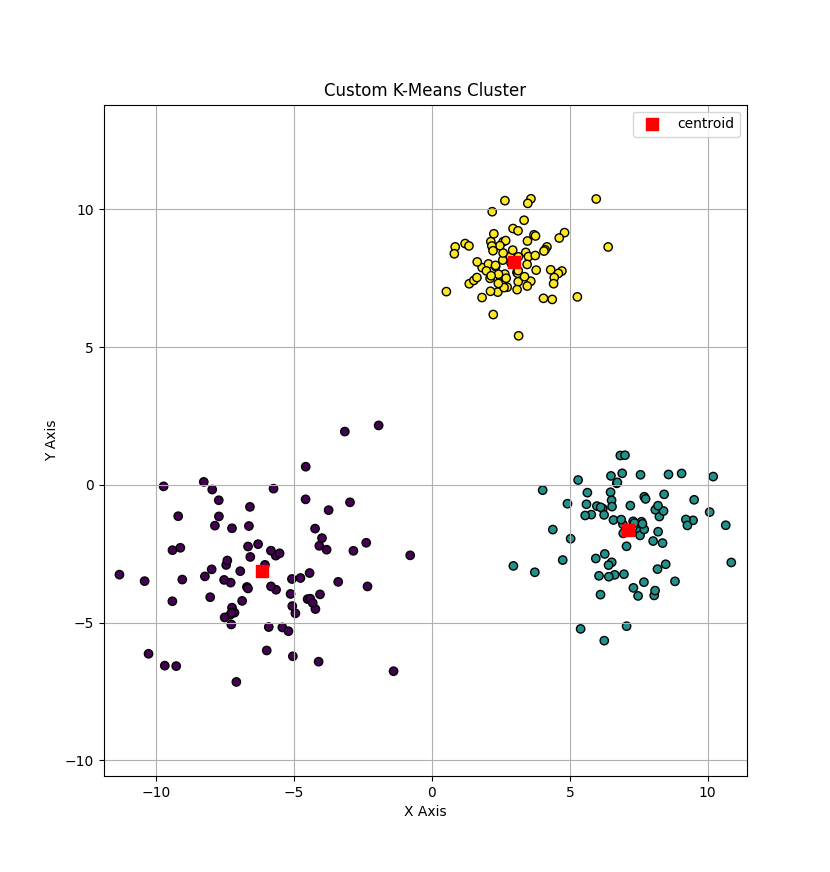
聚类效果如下所示

基于SKlearn的使用

实际开发中可直接使用SKlearn提供的K-Means算法实现。需要注意的是：SKlearn库的KMeans实例只支持使用欧氏距离，不可使用其他距离度量方式

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

def load_data():
    """
    构造测试数据
    """
    # 固定种子，为了可重复
    np.random.seed(996)
    data = np.vstack((
        # 生成形状为（80,2）、满足正态分布的随机数
        np.random.randn(80, 2) + np.array([3, 8]),
        np.random.randn(80, 2)*1.5 + np.array([7,-2]),
        np.random.randn(80, 2)*2 + np.array([-6, -3])
    ))
    return data


def plot(data, centroids, cluster_res):
    """
    可视化
    """
    # 样本是边缘色为黑色的、o形的点
    plt.scatter(data[:,0], data[:,1], c=cluster_res, cmap='viridis', marker='o', edgecolor='k')
    # 质心为红色的、方形的点
    plt.scatter(centroids[:,0], centroids[:,1], c='red', marker='s', s=70, label='centroid')
    # 添加标题、轴标签
    plt.title('K-Means Cluster Using SKlearn')
    plt.xlabel('X Axis')
    plt.ylabel('Y Axis')
    # 添加图例
    plt.legend()
    # 显示网格线
    plt.grid(True)
    # X、Y轴比例相等
    plt.axis("equal")
    # 显示图形
    plt.show()


if __name__ == "__main__":
    data = load_data()
    k = 3
    # 创建KMeans实例，并指定簇的数量，距离度量为欧式距离
    kmeans = KMeans(n_clusters=k)
    # 聚类
    kmeans.fit(data)

    # 获取聚类结果、质心
    cluster_res = kmeans.labels_
    centroids = kmeans.cluster_centers_

    plot(data, centroids, cluster_res)

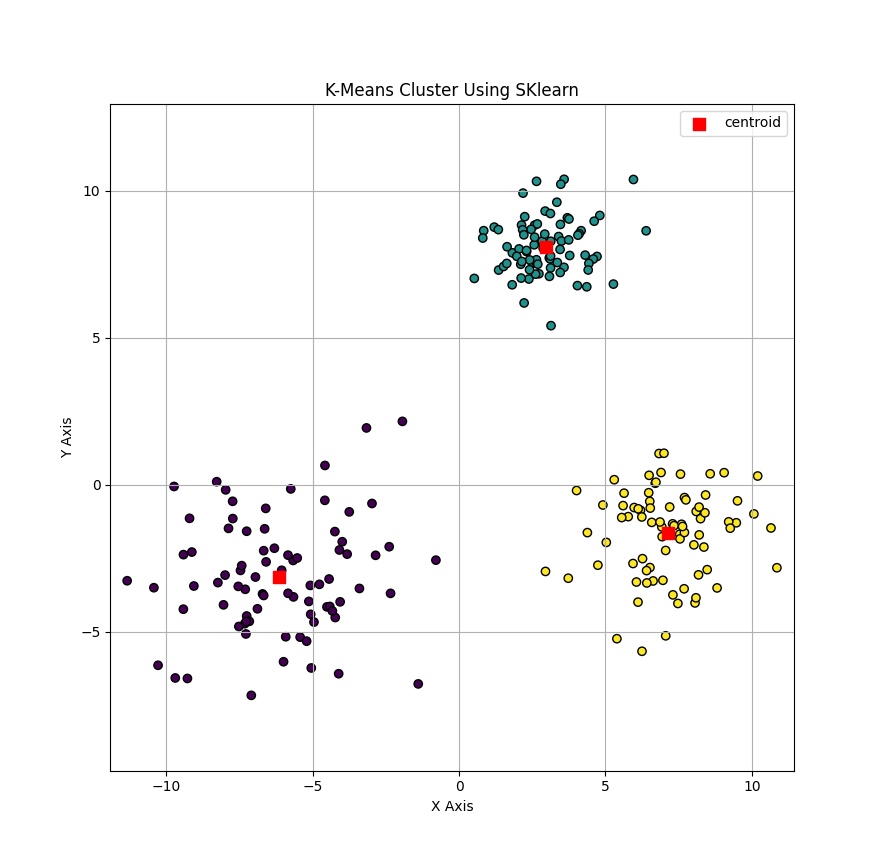
测试结果如下所示

特点

优点

• 无监督学习算法，无需训练集
• 算法简单，易于理解，可解释性强

缺点

• k值选取困难。不合适的k值会产生非预期的结果
• 异常值、噪声敏感：其会影响质心的计算
• 初始选择的k个质心敏感：不同的初始质心可能会导致最终聚类结果发生变化
• 该算法基于距离进行聚类：适用于凸性数据，其能够样本划分为球状类的簇。故对于形状为长条（带状）簇而言不适用该算法

参考文献

• 机器学习 周志华著
• 机器学习公式详解 谢文睿、秦州著
• 图解机器学习和深度学习入门 山口达辉、松田洋之著