xyZGHio

樱花同载酒，终似少年游

0%

机器学习之分类算法：Logistic Regression逻辑回归

发表于 阅读数： 评论数：
本文字数： 6k 阅读时长 ≈ 12 分钟

这里介绍机器学习中用于分类任务的Logistic Regression逻辑回归算法

abstract.png

基本原理

Logistic Regression逻辑回归算法虽然名称中包含回归二字，但其却是一个用于解决二分类问题的分类算法。此外，还可通过某种扩展方法解决多分类问题。该算法是监督学习算法，其底层原理通过Sigmoid函数将广义线性模型GLM(Generalized Linear Model)的结果映射为(0,1)区间范围内。故逻辑回归算法的输出可以理解为将该样本视作正样本的概率。然后通过设定一个阈值（通常为0.5）来判断该样本是否为正样本

由于这里的Sigmoid函数我们通常选用Logistic Function逻辑函数，而广义线性模型又是对线性回归模型的的拓展，故该模型被称为逻辑回归

这里我们先给Logistic Function逻辑函数的定义和图像特征

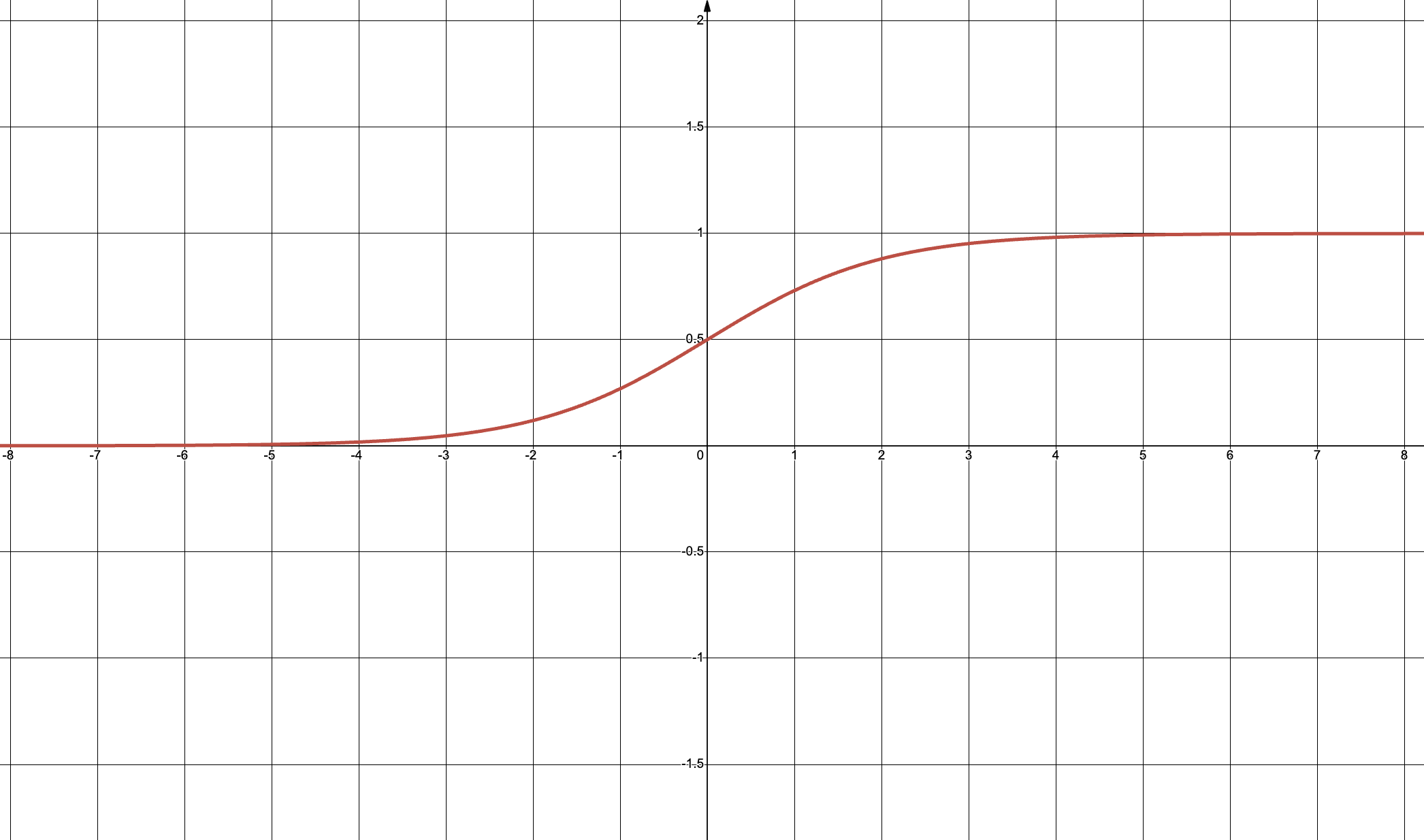
figure 1.png

然后将线性模型代入Logistic Function逻辑函数后，不难得出逻辑回归模型的定义。其中：w是权重向量、x为输入特征向量、b为偏置项。P(y=1|x)表示在给定输入特征向量x的条件下，目标变量y等于1的概率

然后设定一个阈值θ（通常为0.5）进行分类决策。当P(y=1|x)≥θ时，预测y为1，即为正样本；当P(y=1|x)<θ时，预测y为0，即为负样本

至此不难看出，逻辑回归的本质是找出一个线性组合，用作决策边界来分隔样本空间。使得在决策边界某一侧的样本被分类为一个类别，而在决策边界另一侧的样本则被分类为另一个类别。具体地：

  • 一维空间下，输入特征向量x只有一个特征x1。决策边界方程为w1·x1+b=0。其可以表示为在x1轴上的一个点。故决策边界就是一个点
  • 二维空间下，输入特征向量x有两个特征x1、x2。决策边界方程为w1·x1+w2·x2+b=0。其可以表示为在x1-x2平面上的一条直线。故决策边界就是一条直线
  • 三维空间下，输入特征向量x有三个特征x1、x2、x3。决策边界方程为w1·x1+w2·x2+w3·x3+b=0。其可以表示为在x1-x2-x3空间上的一个平面。故决策边界就是一个平面
  • 在四维空间下，输入特征向量x有四个特征x1、x2、x3、x4。决策边界方程为w1·x1+w2·x2+w3·x3+w4·x4+b=0。其可以表示为在x1-x2-x3-x4四维空间上的一个超平面，故决策边界就是一个超平面
  • 在更高维空间下同理，该决策边界也是一个超平面

实践

这里通过SKlearn提供的Logistic Regression逻辑回归模型来实现一个简单的二分类任务

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D


def load_data():
    """
    构造数据集
    """
    # 固定种子，保证可重复
    np.random.seed(42)
    X = np.random.randn(100, 2) 
    # 标签值
    y = ((X[:, 0]+X[:, 1])>0).astype(int)
    return X, y


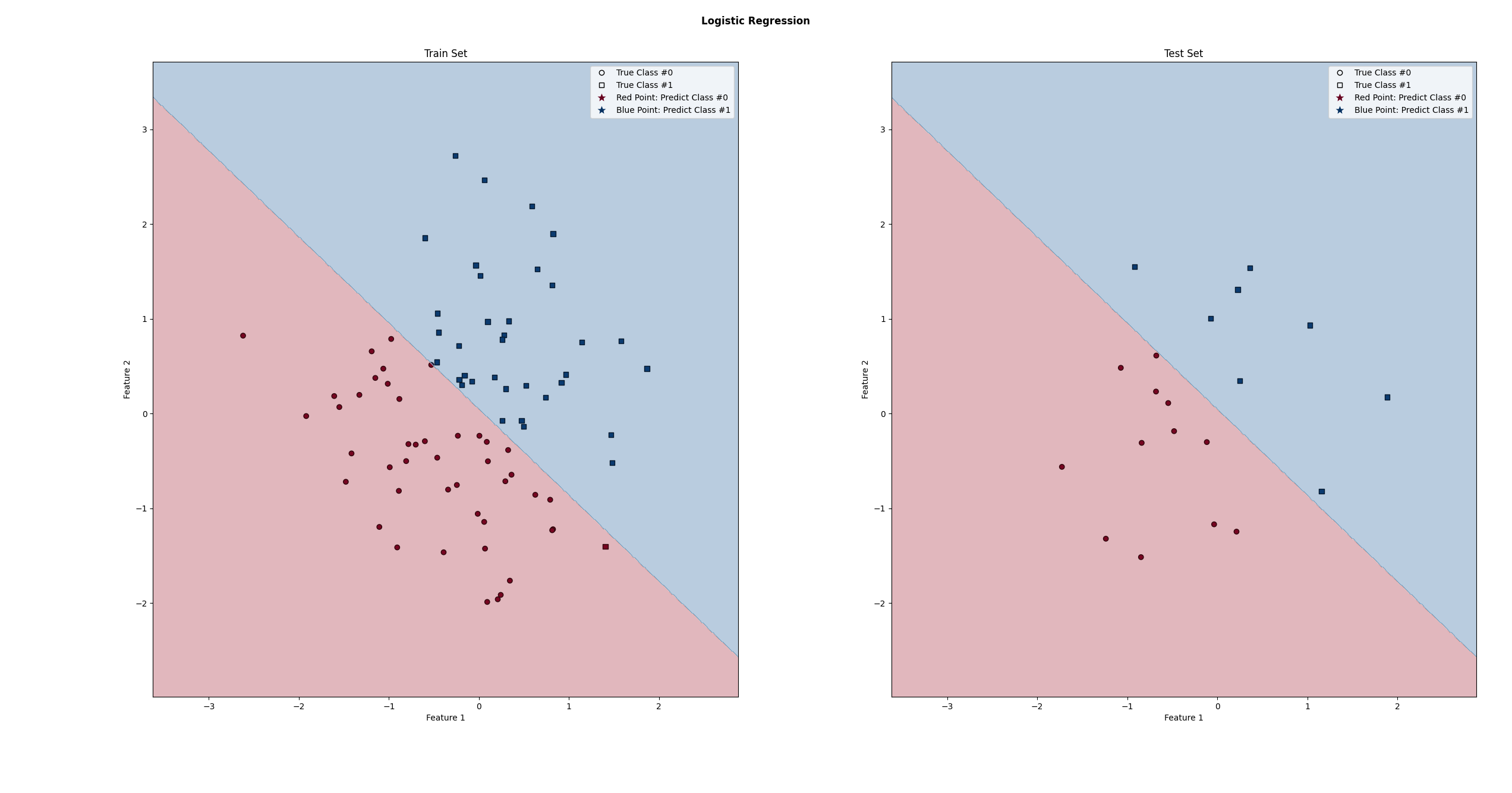
def plot(X_train, y_train, y_train_pred, X_test, y_test, y_test_pred, model):
    """
    可视化
    X_train、y_train、y_train_pred: 训练集的输入、标签、预测值
    X_test、y_test、y_test_pred: 测试集的输入、标签、预测值
    model: 训练后的模型
    """
    # 创建一个包含两个子图的Figure, 其中子图的布局为1行2列
    # 返回：Figure对象、包含子图轴Axes对象的数组
    fig, axes = plt.subplots(1, 2)

    # 可视化 训练集
    # 训练集中真实分类为0的样本索引
    class_0_row_index = y_train==0
    # 训练集中真实分类为1的样本索引
    class_1_row_index = y_train==1
    # 真实分类为0的样本使用圆形表示。预测分类为0的使用红色、预测结果为1的使用蓝色
    axes[0].scatter(X_train[class_0_row_index,0], X_train[class_0_row_index, 1], marker='o', c=y_train_pred[class_0_row_index], cmap=plt.cm.RdBu, edgecolor='k', label='Class #0',vmin=0, vmax=1)
    # 真实分类为1的样本使用方形表示。预测分类为0的使用红色、预测分类为1的使用蓝色
    axes[0].scatter(X_train[class_1_row_index, 0], X_train[class_1_row_index, 1], marker='s', c=y_train_pred[class_1_row_index], cmap=plt.cm.RdBu, edgecolor='k', label='Class #1',vmin=0, vmax=1)
    # 设置X轴标签、Y轴标签、标题
    axes[0].set_xlabel('Feature 1')
    axes[0].set_ylabel('Feature 2')
    axes[0].set_title('Train Set')

    # 可视化 测试集
    # 测试集中真实分类为0的样本索引
    class_0_row_index = y_test==0
    # 测试集中真实分类为1的样本索引
    class_1_row_index = y_test==1
    # 真实分类为0的样本使用圆形表示。预测分类为0的使用红色、预测结果为1的使用蓝色
    axes[1].scatter(X_test[class_0_row_index, 0], X_test[class_0_row_index, 1], marker='o', c=y_test_pred[class_0_row_index], cmap=plt.cm.RdBu, edgecolor='k', label='Class #0',vmin=0, vmax=1)
    # 真实分类为1的样本使用方形表示。预测分类为0的使用红色、预测分类为1的使用蓝色
    axes[1].scatter(X_test[class_1_row_index, 0], X_test[class_1_row_index, 1], marker='s',c=y_test_pred[class_1_row_index], cmap=plt.cm.RdBu, edgecolor='k', label='Class #1',vmin=0, vmax=1)
    # 设置X轴标签、Y轴标签、标题
    axes[1].set_xlabel('Feature 1')
    axes[1].set_ylabel('Feature 2')
    axes[1].set_title('Test Set')

    # 创建自定义图例
    legend_elements = [
        # 圆形散点 表示 真实分类为0
        Line2D([],[], marker='o', markeredgecolor='k', markerfacecolor='none', color="none", label='True Class #0'),
        # 方形散点 表示 真实分类为1
        Line2D([],[], marker='s', markeredgecolor='k', markerfacecolor='none', color="none", label='True Class #1'),
        # 红色散点 表示 预测分类为0
        Line2D([],[], marker='*', markerfacecolor=plt.cm.RdBu(0.0), markersize=10, markeredgecolor='none', color="none", label='Red Point: Predict Class #0'),
        # 蓝色散点 表示 预测分类为1
        Line2D([],[], marker='*', markerfacecolor=plt.cm.RdBu(1.0), markersize=10, markeredgecolor='none', color="none", label='Blue Point: Predict Class #1')
    ]
    # 添加图例
    axes[0].legend(handles=legend_elements)
    axes[1].legend(handles=legend_elements)

    # 计算输入样本在X轴、Y轴的边界
    data = np.vstack((X_train, X_test))
    x_range = data[:,0].min() - 1, data[:,0].max() + 1
    y_range = data[:,1].min() - 1, data[:,1].max() + 1
    # 可视化 决策边界
    plot_decision_boundary(x_range, y_range, model, axes)

    # 自动调整子图的布局间距
    plt.tight_layout()
    # 设置Figure标题
    fig.suptitle("Logistic Regression", fontweight='bold')
    # 显示图形
    plt.show()


def plot_decision_boundary(x_range, y_range, model, axes):
    """
    绘制决策边界
    """
    # X轴的范围
    x_min, x_max = x_range
    # Y轴的范围
    y_min, y_max = y_range 

    # 创建二维网格的x、y坐标
    mesh_x, mesh_y = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
    # 网格点的x、y坐标
    mesh_xy = np.hstack((mesh_x.ravel()[:, np.newaxis], mesh_y.ravel()[:, np.newaxis]))
    # 计算每个网格点的预测分类, 并调整成网格的形状
    mesh_z = lr_model.predict(mesh_xy)
    mesh_z = mesh_z.reshape(mesh_x.shape)

    # 绘制填充等高线图。其中，填充颜色的alpha透明度为0.3
    axes[0].contourf(mesh_x, mesh_y, mesh_z, alpha=0.3, cmap=plt.cm.RdBu)
    axes[1].contourf(mesh_x, mesh_y, mesh_z, alpha=0.3, cmap=plt.cm.RdBu)


if __name__ == "__main__":
    # 加载数据集
    X, y = load_data()
    # 划分训练集、测试集，比例为4:1。固定random_state种子保证每次划分结果一样，可重复
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=996)

    # 创建逻辑回归LR模型实例
    lr_model = LogisticRegression()
    # 使用训练集训练模型，阈值固定使用0.5
    lr_model.fit(X_train, y_train)
    # 输出模型参数
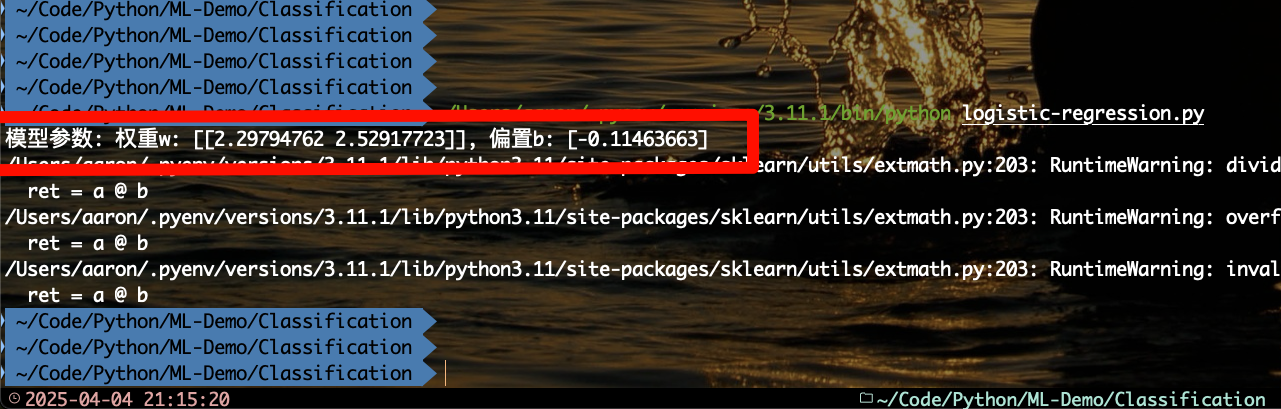
    print(f"模型参数: 权重w: {lr_model.coef_}, 偏置b: {lr_model.intercept_}")

    # 预测训练集
    y_train_pred = lr_model.predict(X_train)
    # 预测测试集
    y_test_pred = lr_model.predict(X_test)

    # 可视化
    plot(X_train, y_train, y_train_pred, X_test, y_test, y_test_pred, lr_model)

训练后，模型参数结果如下

figure 2.png

分类效果如下

figure 3.png

特点

优点

  • 模型的权重参数可以解释每个特征对目标变量的影响，可解释性强
  • 模型简单，计算量小
  • 模型的输出结果是一个概率。一方面，实际业务中可通过调整阈值来灵活调整分类决策；另一方面，其在医学诊断、风险评估等需要概率估计的场景非常有用
  • 该模型不要求样本严格的线性可分。即使在近似线性可分的条件下，最终结果在一定程度上也可以满足实际的业务需求

缺点

  • 对异常值敏感
  • 对于明显非线性可分的样本，该模型无法达到预期效果

参考文献

  • 机器学习 周志华著
  • 机器学习公式详解 谢文睿、秦州著
  • 图解机器学习和深度学习入门 山口达辉、松田洋之著
推荐文章
请我喝杯咖啡捏～

欢迎关注我的微信公众号：青灯抽丝