xyZGHio

樱花同载酒，终似少年游

0%

机器学习之分类算法：Naive Bayes朴素贝叶斯分类

发表于 阅读数： 评论数：
本文字数： 7.7k 阅读时长 ≈ 15 分钟

这里介绍机器学习中常见的一种分类算法——Naive Bayes朴素贝叶斯分类

abstract.png

基本原理

贝叶斯定理

贝叶斯公式的形式很简单，其描述了两个事件条件概率之间的关系

现在我们以分类任务为例，将样本特征X、分类类别C代入上式，可得

其中：

  • P(C)：表示分类类别C出现的概率，其被称为先验概率。因为这一概率通常可以通过历史数据、先验知识经验获得。例如，当我们抛一枚硬币之前，就知道其出现正面向上的概率为0.5
  • P(X∣C)：表示分类类别为C的情况下，样本特征为X的条件概率
  • P(X)：表示样本特征X出现的概率。其作为分母起到了归一化的作用，使得所有后验概率之和为1
  • P(C|X)：表示样本特征为X的情况下，分类类别为C的条件概率。其被称为后验概率。其含义也很好理解，表示在给定特征的情况下，其属于某个类别的概率有多大

朴素贝叶斯分类

朴素贝叶斯分类是一种监督学习的分类算法。具体地：

训练阶段：通过训练集，直接统计样本对应的类别，即可计算、存储先验概率P(C)。同时，还需要通过计算、存储所有的条件概率P(X∣C)。而对于P(X)而言，则可利用下面的全概率公式进行计算。但在实际分类应用中，P(X)可不计算。因为，分类决策是基于后验概率P(C∣X)的相对大小得出。而对于一个给定样本而言，P(X)则是一个常数，对所有分类类别都是一样的。故，并不会影响类别之间概率的相对大小

推理阶段：按需取出相应的概率，直接利用贝叶斯公式计算该测试样本特征在不同分类结果下的后验概率。其中，后验概率最大对应的分类即为该测试样本的预测分类结果

关于朴素的解释

朴素贝叶斯中的朴素来源于Navie一词，该模型其做了一个假设用于简化计算——在给定分类类别C的条件下，样本的所有特征之间是相互独立，即所谓的Conditional Independence 条件独立。例如，特征向量X={x1,x2,x3,x4}。根据条件独立这一假设，则可以将联合条件概率的计算简化为对各特征条件概率的计算

虽然在现实世界中，特征之间往往存在一定的关联性，很难完全独立。但即使如此，朴素贝叶斯分类依然在很多实际分类任务中表现良好。现在详细解释下，为什么条件独立假设可以简化计算

假设样本特征X有x1~xn这n个特征，每个特征都有k个可能的取值。分类类别C的所有数量为m。则：

  • 没有条件独立假设：此时计算在某个给定类别C的情况下，所有n个特征的联合条件概率。即：k^n 个。m个分类类别的话则有：k^n*m 个
  • 具备条件独立假设：此时只需计算在给定类别C的情况下，n个特征各自的条件概率。即：k*n 个。m个分类类别的话则有：k*n*m 个

从上不难看出，如果没有条件独立假设，条件概率的计算量会呈指数级进行增长

需要注意，朴素贝叶斯所做的假设是Conditional Independence 条件独立，而不是 Independence 独立。所以，对于特征向量X={x1,x2,x3,x4}而言，采用下式计算P(X)是错误的。因为下式成立的前提是特征间相互独立

实践

离散型特征

训练集

这里举一个判断西瓜是否甜的例子，来说明朴素贝叶斯分类的整个过程。我们选择的特征有：x1敲击声音（清脆、沉闷）、x2瓜皮颜色（黑绿、黄白）。显然这里的特征是离散型特征，训练集样本如下所示

编号 x1 敲击声音 x2 瓜皮颜色 分类
#1 清脆 黑绿 甜
#2 清脆 黑绿 甜
#3 清脆 黑绿 甜
#4 清脆 黑绿 甜
#5 沉闷 黑绿 甜
#6 清脆 黑绿 不甜
#7 沉闷 黑绿 不甜
#8 沉闷 黄白 不甜
#9 沉闷 黄白 不甜

计算先验概率P(C)

不难有：

  • 分类甜：样本有5个（样本编号：#1～#5），P(甜) = 5/9
  • 分类不甜：样本有4个（样本编号：#6～#9），P(不甜) = 4/9

计算敲击声音的条件概率

现在我们来计算所有的条件概率P(X|C)。根据条件独立假设，我们只需计算各特征的条件概率即可

计算x1特征敲击声音的条件概率P(x1|C)：

  • 分类甜的条件下，敲击声音为清脆的样本有4个（样本编号：#1～#4），P(清脆|甜) = 4/5 = 0.8
  • 分类甜的条件下，敲击声音为沉闷的样本有1个（样本编号：#5），P(沉闷|甜) = 1/5 = 0.2
  • 分类不甜的条件下，敲击声音为清脆的样本有1个（样本编号：#6），P(清脆|不甜) = 1/4 = 0.25
  • 分类不甜的条件下，敲击声音为沉闷的样本有3个（样本编号：#7～#9），P(沉闷|不甜) = 3/4 = 0.75

计算瓜皮颜色的条件概率

由于训练集的所有样本中，黄白瓜皮的西瓜在甜分类下从未出现过。即：P(黄白|甜)=0。这样不仅会使得联合条件概率P(x1,x2=黄白|甜)为零，后验概率最终也为0。从而影响分类效果。即所谓的零概率问题

解决办法也很简单，对x2瓜皮颜色特征进行平滑处理即可。平滑处理不仅可以解决零概率问题，还可以增强模型的泛化能力。这里我们使用拉普拉斯平滑。其中：n(x2,C)表示特征x2在类别C中出现的次数，n(C)表示类别C出现的次数，V则为特征x2所有可能的取值数量。从下式不难看出，其本质就是通过对分子加一保证x2特征中的任何取值都至少出现1次，避免零概率问题。同时，为了保证x2特征的条件概率之和为1，分母加了特征x2所有可能取值的数量

这里，由于x2特征取值有黑绿、黄白两种颜色，故上式中的V值为2。计算x2特征瓜皮颜色的条件概率P(x2|C)：

  • 分类甜的条件下，瓜皮颜色为黑绿的样本有5个（样本编号：#1～#5），P(黑绿|甜) = (5+1)/(5+2) = 6/7
  • 分类甜的条件下，瓜皮颜色为黄白的样本有0个，P(黄白|甜) = (0+1)/(5+2) = 1/7
  • 分类不甜的条件下，瓜皮颜色为黑绿的样本有2个（样本编号：#6、#7），P(黑绿|不甜) = (2+1)/(4+2) = 0.5
  • 分类不甜的条件下，瓜皮颜色为黄白的样本有2个（样本编号：#8、#9），P(黄白|不甜) = (2+1)/(4+2) = 0.5

计算P(X)

根据全概率公式，结合条件独立假设，不难有：

故：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
P(清脆,黑绿) = P(清脆|甜)·P(黑绿|甜)·P(甜) + P(清脆|不甜)·P(黑绿|不甜)·P(不甜)
            = 0.8 * 6/7 * 5/9 + 0.25 * 0.5 * 4/9
            = 0.4365079365

P(清脆,黄白) = P(清脆|甜)·P(黄白|甜)·P(甜) + P(清脆|不甜)·P(黄白|不甜)·P(不甜)
            = 0.8 * 1/7 * 5/9 + 0.25 * 0.5 * 4/9
            = 0.119047619

P(沉闷,黑绿) = P(沉闷|甜)·P(黑绿|甜)·P(甜) + P(沉闷|不甜)·P(黑绿|不甜)·P(不甜)
            = 0.2 * 6/7 * 5/9 + 0.75 * 0.5 * 4/9
            = 0.2619047619

P(沉闷,黄白) = P(沉闷|甜)·P(黄白|甜)·P(甜) + P(沉闷|不甜)·P(黄白|不甜)·P(不甜)
            = 0.2 * 1/7 * 5/9 + 0.75 * 0.5 * 4/9
            = 0.1825396825

测试

至此，针对上述训练集而言。Naive Bayes朴素贝叶斯分类器的所有模型参数全部训练完成了，现在我们来测试下

Case 1：测试样本特征：清脆、黑绿

1
2
3
4
5
6
7
8
9
P(甜|清脆,黑绿) = P(清脆,黑绿|甜)·P(甜)/P(清脆,黑绿)
             = P(清脆|甜)·P(黑绿|甜)·P(甜)/P(清脆,黑绿)
             = (0.8 * 6/7 * 5/9) / 0.4365079365
             = 0.8727272727
             
P(不甜|清脆,黑绿) = P(清脆,黑绿|不甜)·P(不甜)/P(清脆,黑绿)
             = P(清脆|不甜)·P(黑绿|不甜)·P(不甜)/P(清脆,黑绿)
             = (0.25 * 0.5 * 4/9) / 0.4365079365
             = 0.1272727273

由于：P(甜|清脆,黑绿) > P(不甜|清脆,黑绿)。故这个测试样本的分类预测结果为甜。这个测试结果和测试样本#1～#4也是符合的

Case 2：测试样本特征：清脆、黄白

1
2
3
4
5
6
7
8
9
P(甜|清脆,黄白) = P(清脆,黄白|甜)·P(甜)/P(清脆,黄白)
             = P(清脆|甜)·P(黄白|甜)·P(甜)/P(清脆,黄白)
             = (0.8 *  1/7 * 5/9) / 0.119047619
             = 0.5333333335
             
P(不甜|清脆,黄白) = P(清脆,黄白|不甜)·P(不甜)/P(清脆,黄白)
             = P(清脆|不甜)·P(黄白|不甜)·P(不甜)/P(清脆,黄白)
             = (0.25 * 0.5 * 4/9) / 0.119047619
             = 0.4666666669

由于：P(甜|清脆,黄白) > P(不甜|清脆,黄白)。故这个瓜的分类预测结果为甜。这个Case也体现了拉普拉斯平滑的作用。如果不进行平滑处理，则P(黄白|甜)=0，进而导致P(甜|清脆,黄白)为0

Case 3：测试样本特征：沉闷、黑绿

1
2
3
4
5
6
7
8
9
P(甜|沉闷,黑绿) = P(沉闷,黑绿|甜)·P(甜)/P(沉闷,黑绿)
             = P(沉闷|甜)·P(黑绿|甜)·P(甜)/P(沉闷,黑绿)
             = (0.2 * 6/7 * 5/9) / 0.2619047619
             = 0.3636363636
             
P(不甜|沉闷,黑绿) = P(沉闷,黑绿|不甜)·P(不甜)/P(沉闷,黑绿)
             = P(沉闷|不甜)·P(黑绿|不甜)·P(不甜)/P(沉闷,黑绿)
             = (0.75 * 0.5 * 4/9) / 0.2619047619
             = 0.6363636364

由于：P(甜|沉闷,黑绿) < P(不甜|沉闷,黑绿)。故这个瓜的分类预测结果为不甜。这个测试结果和测试样本#7也是符合的

Case 4：测试样本特征：沉闷、黄白

1
2
3
4
5
6
7
8
9
P(甜|沉闷,黄白) = P(沉闷,黄白|甜)·P(甜)/P(沉闷,黄白)
             = P(沉闷|甜)·P(黄白|甜)·P(甜)/P(沉闷,黄白)
             = (0.2 * 1/7 * 5/9) / 0.1825396825
             = 0.08695652176

P(不甜|沉闷,黄白) = P(沉闷,黄白|不甜)·P(不甜)/P(沉闷,黄白)
             = P(沉闷|不甜)·P(黄白|不甜)·P(不甜)/P(沉闷,黄白)
             = (0.75 * 0.5 * 4/9) / 0.1825396825
             = 0.9130434785

由于：P(甜|沉闷、黄白) < P(不甜|沉闷、黄白)。故这个瓜的分类预测结果为不甜。这个测试结果和测试样本#8、#9也是符合的

连续型特征

当特征是连续变量时，处理方式与离散变量有所不同。从上述西瓜的例子中，进一步证实，贝叶斯公式中的分母部分不会影响最终的分类决策结果。故对于连续型特征而言，由于分母部分的计算较为复杂，所以通常不进行计算。且对于连续型特征而言，我们通常会假设该特征服从某种概率分布，这里以最常见的高斯分布为例来进行说明。由于连续变量在任意一个点上的概率实际上是0。故在计算条件概率会使用概率密度函数PDF来进行代替。下式中的均值、标准差表示的是某特征xi在指定分类类别c下的均值、标准差

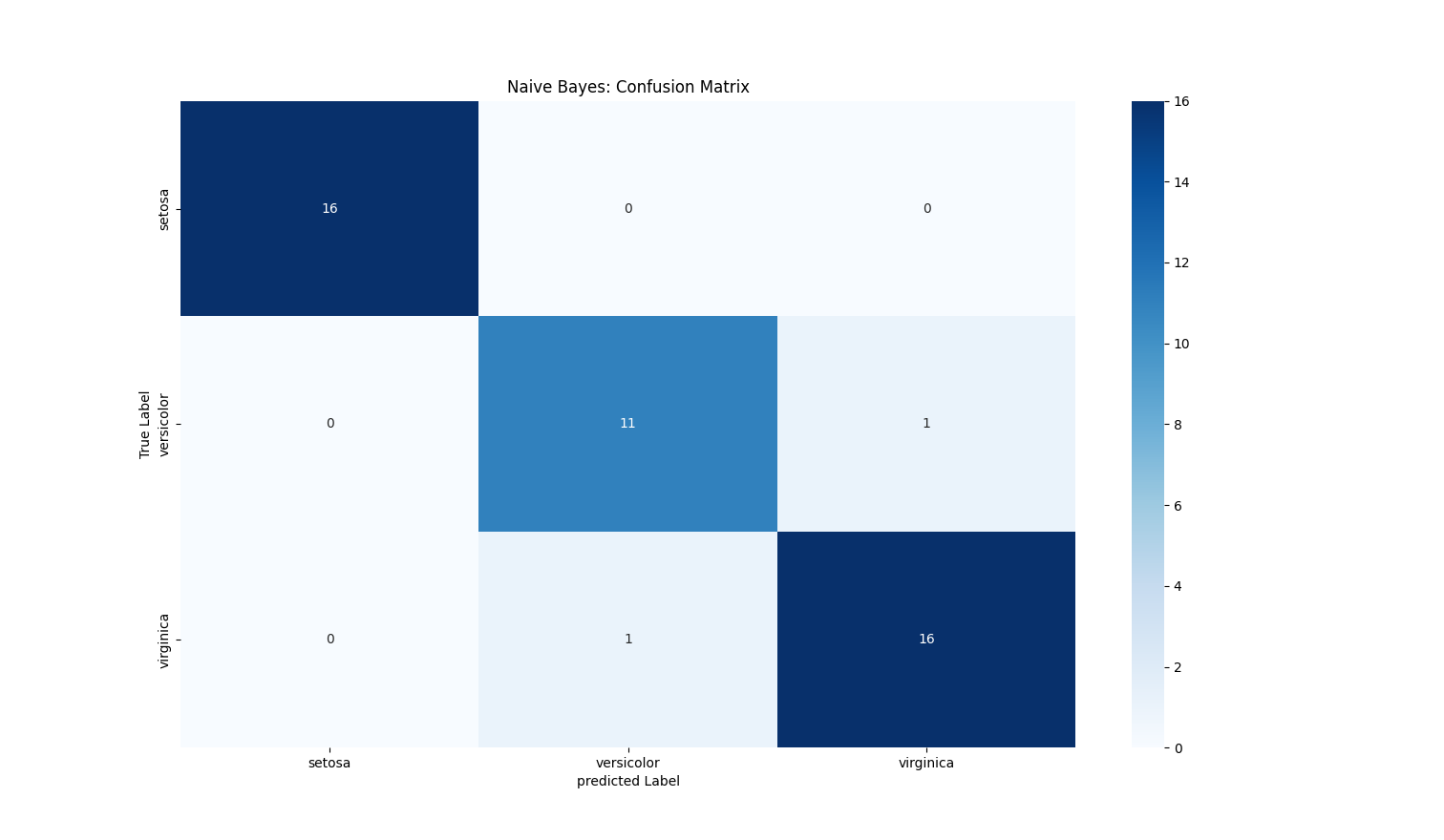
下面通过SKlearn提供的高斯朴素贝叶斯分类器来实现一个分类任务。这里选用为经典的鸢尾花Iris数据集。该数据集包含150个样本，选取了鸢尾花的四个特征（sepal length花萼长度、sepal width花萼宽度、petal length花瓣长度、petal width花瓣宽度）用于预测鸢尾花的品种（setosa/versicolor/virginica）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix
import seaborn as sns
from sklearn.metrics import classification_report

# 加载数据集: 鸢尾花
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 特征名称
feature_names = iris.feature_names
# 类别名称
label_names = iris.target_names

# 划分训练集、测试集，比例为7:3。固定random_state种子保证每次划分结果一样，可重复
X_train, X_test, y_train, y_test = train_test_split(X, y ,test_size=0.3, random_state=69)

# 创建高斯朴素贝叶斯分类器实例
gnb = GaussianNB()

# 使用训练集训练模型
gnb.fit(X_train, y_train)

# 打印模型参数
for c_index in range(len(label_names)):
    print(f"----------------------- 类别: {label_names[c_index]} ----------------------")
    for x_index in range(len(feature_names)):
        print(f"特征{feature_names[x_index]: ^21} ==>> 均值: {gnb.theta_[c_index][x_index]:.4f} 方差: {gnb.var_[c_index][x_index]:.4f}")
    print("\n")

# 预测测试集
y_pred = gnb.predict(X_test)

# 计算评估指标
report = classification_report(y_test, y_pred, target_names=label_names)
print(f"------------------------ 评估指标 ------------------------")
print(f"{report}")

# 计算混淆矩阵
confusion_matrix = confusion_matrix(y_true=y_test,y_pred=y_pred)

# 绘制混淆矩阵
# annot=True: 每个单元格显示数值; fmt="d": 单元格数值格式为整数
# xticklabels / yticklabels: 设置X轴/Y轴的刻度标签名称
sns.heatmap(confusion_matrix, annot=True, cmap="Blues", fmt="d", xticklabels=label_names, yticklabels=label_names)
# X轴标题：预测标签
plt.xlabel("predicted Label")
# Y轴标题：真实标签
plt.ylabel("True Label")
plt.title("Naive Bayes: Confusion Matrix")
plt.show()

输出结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
----------------------- 类别: setosa ----------------------
特征  sepal length (cm)   ==>> 均值: 4.9882 方差: 0.0922
特征  sepal width (cm)    ==>> 均值: 3.3912 方差: 0.1167
特征  petal length (cm)   ==>> 均值: 1.4735 方差: 0.0349
特征  petal width (cm)    ==>> 均值: 0.2559 方差: 0.0125


----------------------- 类别: versicolor ----------------------
特征  sepal length (cm)   ==>> 均值: 5.9316 方差: 0.2422
特征  sepal width (cm)    ==>> 均值: 2.7263 方差: 0.0983
特征  petal length (cm)   ==>> 均值: 4.2237 方差: 0.2423
特征  petal width (cm)    ==>> 均值: 1.3263 方差: 0.0393


----------------------- 类别: virginica ----------------------
特征  sepal length (cm)   ==>> 均值: 6.5818 方差: 0.4154
特征  sepal width (cm)    ==>> 均值: 2.9727 方差: 0.1093
特征  petal length (cm)   ==>> 均值: 5.5091 方差: 0.2887
特征  petal width (cm)    ==>> 均值: 1.9879 方差: 0.0641


------------------------ 评估指标 ------------------------
              precision    recall  f1-score   support

      setosa       1.00      1.00      1.00        16
  versicolor       0.92      0.92      0.92        12
   virginica       0.94      0.94      0.94        17

    accuracy                           0.96        45
   macro avg       0.95      0.95      0.95        45
weighted avg       0.96      0.96      0.96        45

figure 1.png

参考文献

  • 机器学习 周志华著
  • 机器学习公式详解 谢文睿、秦州著
  • 图解机器学习和深度学习入门 山口达辉、松田洋之著
推荐文章
请我喝杯咖啡捏～

欢迎关注我的微信公众号：青灯抽丝