数据预处理作为机器学习中的关键一环，这里介绍其中的Outlier Analysis异常值分析

异常值检测

IQR法，又被称为四分位距法。其是一种基于四分位数的异常值检测方法。四分位数，相对于均值、标准差等指标而言，其不易受到极端异常值的影响。其中：

第一四分位数Q1：又称为下四分位数。其是数据集的第25百分位数。即：数据集中有25%的数据小于等于它
第二四分位数Q2：又被称之为中位数。其是数据集的第50百分位数。即：数据集中有50%的数据小于等于它
第三四分位数Q3：又称为上四分位数。其是数据集的第75百分位数。即：数据集中有75%的数据小于等于它

IQR 四分位距（Interquartile Range）指的是上四分位数（Q3）与下四分位数（Q1）之间的差值。显然该指标衡量的是数据集中间那50%的数据的分布宽度。该指标忽略了数据两端的极端值，而聚集于核心部分

$\mathbf{IQR} = \mathbf{Q3} - \mathbf{Q1}$

进一步地，IQR法定义了一个合理数据的上下限。对于超过这个界限的数据，我们就可以认为是Outlier异常值。具体如下。其中，IQR前的系数通常取统计学上的经验值1.5

合理数据的上限 W_upper ：Q3 + 1.5 * IQR
合理数据的下限 W_lower ：Q1 - 1.5 * IQR

下面使用Pandas、Seaborn来展示如何使用IQR检测、识别数据集中的异常值，并绘制箱线图进行可视化展示。其中箱线图的含义如下：

箱体的下边缘：即箱底，表示第一四分位数 Q1
箱体的上边缘：即箱顶，表示第三四分位数 Q3
箱内的横线：表示第二四位数Q2，即中位数
箱体的高度：表示IQR四分位距
上须线的末端：表示数据集中不超过上限W_upper的最大样本值。即：max{x ∣ x ≤ W_upper}
下须线的末端：表示数据集中不低于下限W_lower的最小样本值。即：min{x ∣ x ≥ W_lower}
超过上下限范围[W_lower,W_upper]的数据点：表示异常值

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.ticker import MultipleLocator


data = {
    "student" : ["张一","张二","张三","张四","张五","张六","张七","张八","张九","李一","李二","王一","王二","王三"],
    "score" : [88,82,99,92,69,93,222,77,17,-4,-7,170,60,67]
    }
df = pd.DataFrame(data)
print(f"Origin Data: \n{df}")
print("-"*80)


# 计算Q1、Q3、IQR
Q1 = df["score"].quantile(0.25)
Q3 = df["score"].quantile(0.75)
IQR = Q3 - Q1
print(f"Q1 : {Q1},  Q3 : {Q3},  IQR: {IQR}")

# 合理的数据的上下限
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
print(f"合理的数据区间: [{lower_bound}, {upper_bound}]")
print("-"*80)

# # 异常数据
error_data = df[ (df['score'] < lower_bound) | (df['score'] > upper_bound) ]
print(f"异常数据: \n{error_data}")

# 绘制箱线图
fig, ax = plt.subplots()
# 定义异常值的样式
error_data_style = {
    # 形状: 圆形
    'marker': 'o',
    # 填充: 红色
    'markerfacecolor': 'red',
    # 边框:黑色
    'markeredgecolor': 'black',   
    # 透明度
    'alpha': 0.5
}

# 绘图
# whis: IQR前的系数使用默认的1.5
# color: 设置箱体的颜色
# flierprops: 异常值样式
sns.boxplot(y=df['score'], whis = 1.5, color="#95DEE3", flierprops=error_data_style)

# 设置Y轴刻度为10的倍数
ax.yaxis.set_major_locator(MultipleLocator(10))

# 设置标题
plt.title('Student Score Box')
plt.ylabel('Score')
 # 显示网格线
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()

输出结果如下

Origin Data: 
   student  score
0       张一     88
1       张二     82
2       张三     99
3       张四     92
4       张五     69
5       张六     93
6       张七    222
7       张八     77
8       张九     17
9       李一     -4
10      李二     -7
11      王一    170
12      王二     60
13      王三     67
--------------------------------------------------------------------------------
Q1 : 61.75,  Q3 : 92.75,  IQR: 31.0
合理的数据区间: [15.25, 139.25]
--------------------------------------------------------------------------------
异常数据: 
   student  score
6       张七    222
9       李一     -4
10      李二     -7
11      王一    170

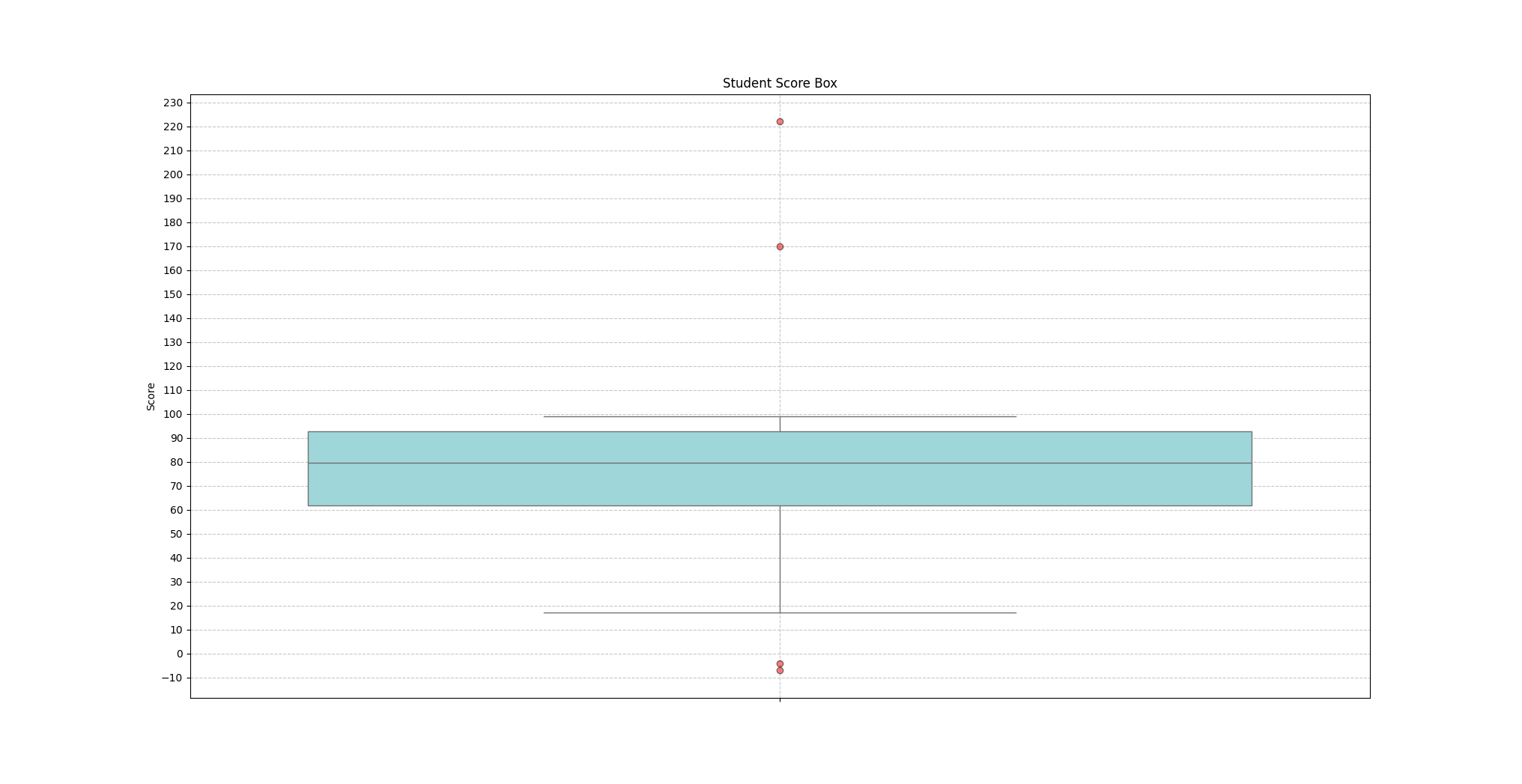
异常值处理

异常值检测出来后，可通过下述常见策略进行处理：

删除：删除包含存在异常值的样本。但这样会导致数据集中样本数量减少
Capping盖帽：将超出边界的异常值直接替换为相应的边界值
替换：将异常值视作为缺失值，然后使用某种策略（均值/众数/中位数）进行填充
Binning分箱：将连续的数值变量转换为离散的类别变量。此时，异常值的具体数值将不再重要。因为其会被归为最高或最低的某个类别中

参考文献

机器学习周志华著
机器学习公式详解谢文睿、秦州著
图解机器学习和深度学习入门山口达辉、松田洋之著

xyZGHio

机器学习之数据预处理：Outlier Analysis异常值分析

异常值检测

异常值处理

参考文献