xyZGHio

樱花同载酒，终似少年游

0%

机器学习之分类算法：SVM（Support Vector Machine）支持向量机

发表于 阅读数： 评论数：
本文字数： 6.1k 阅读时长 ≈ 12 分钟

这里介绍机器学习中的分类算法——SVM（Support Vector Machine）支持向量机

abstract.png

基本原理

SVM（Support Vector Machine）支持向量机是一种监督学习的分类算法。其不仅可以解决二分类问题，还可通过某种扩展方法解决多分类问题。其通过一个线性的决策边界用于区分样本。具体地，在二维空间中该决策边界是一条直线；在三维空间中该决策边界是一个平面；而在更高维空间中该决策边界是一个超平面。例如，对于一个二维空间下的样本集来说，事实上有多条直线都可以将两种类型的样本完美进行划分，但哪一条直线的划分效果才是最好的呢？

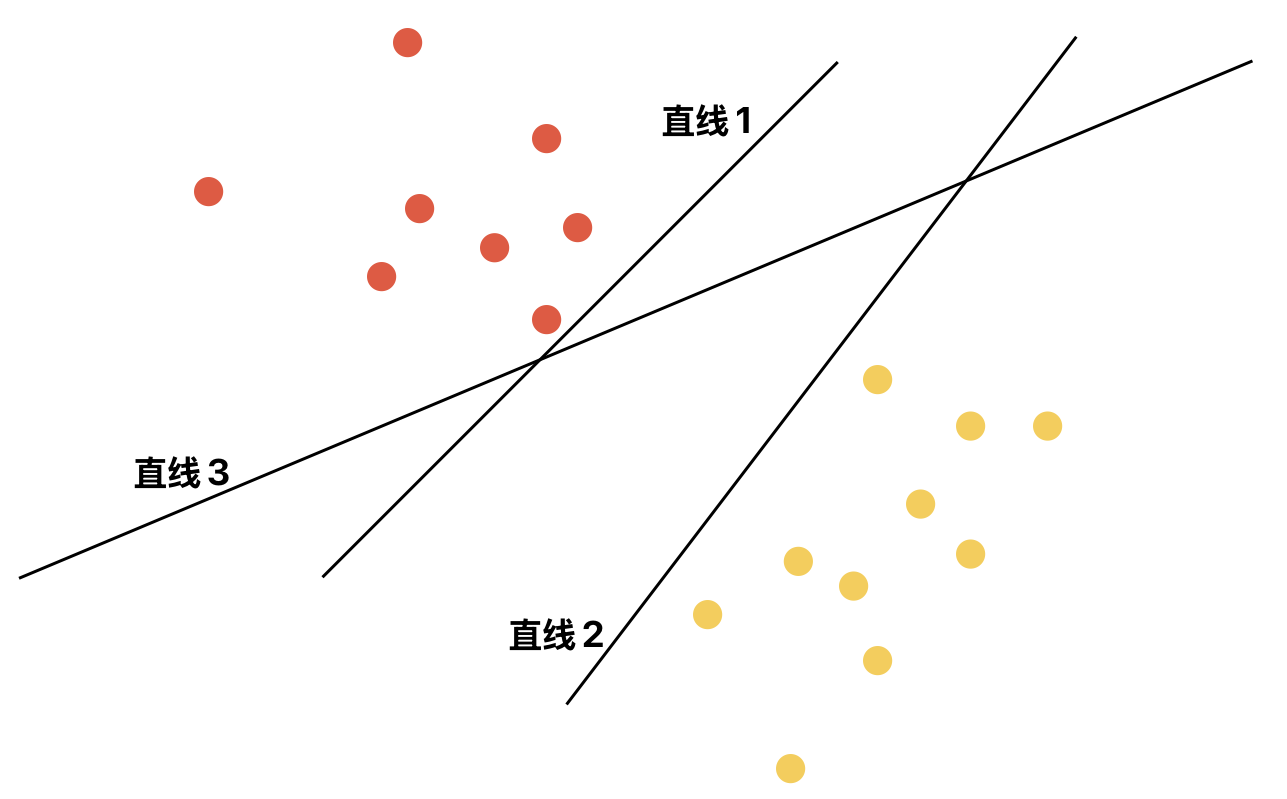
figure 1.png

SVM模型寻找的是 决策边界两侧最近的样本到该边界的距离都最远 的决策边界，即所谓的最大间隔。其中，决策边界两侧最近的样本被称之为Support Vector支持向量。其中原因也很容易理解，决策边界离支持向量越远，其应对样本轻微波动的能力就越强，对新样本的预测表现也越良好，鲁棒性越强、泛化性越高

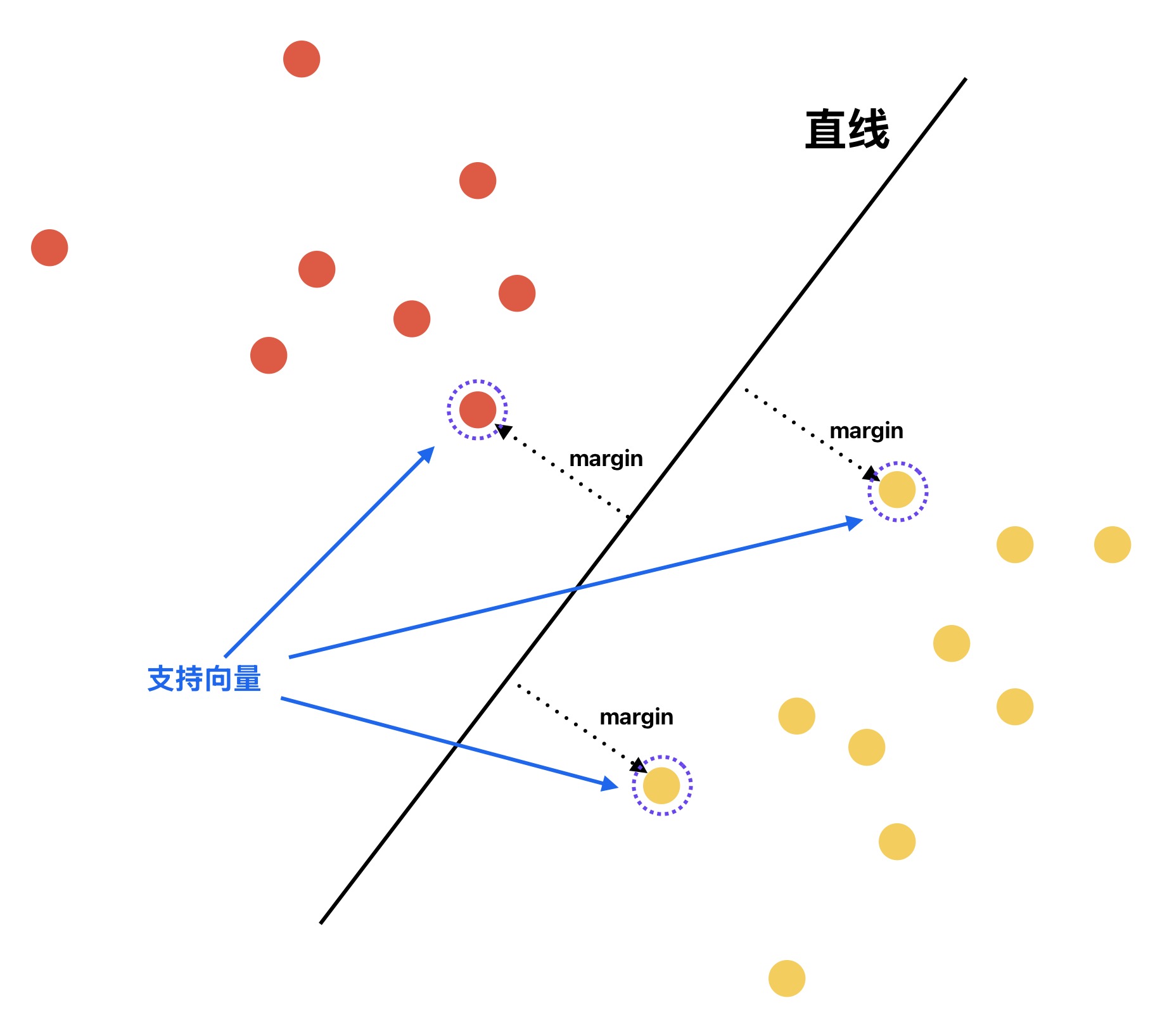
figure 2.jpg

事实上，SVM的训练过程本质就是一个数学上的优化问题——Quadratic Programming二次规划问题。其优化目标是找到一个最大间隔的超平面作为决策边界，使得两类样本之间的间隔最大化。故其在训练计算时需要遍历所有样本，用于确定最终决策边界及该决策边界对应的支持向量。而当训练完成后，模型只需存储决策边界的参数、支持向量等信息即可对新样本进行预测，而无需存储全部的训练集数据

软间隔

在数据完全线性可分的条件下，SVM可以找到这样的一个超平面作为决策边界，其不仅可以将两种类型的样本数据完美地分开，并且使间隔最大。即所谓的Hard Margin硬间隔。但事实上很多时候，由于现实数据的复杂性局限性、噪声、异常值等因素，其往往不是完全的线性可分，只是近似的线性可分。这种条件下，作为线性分类器的SVM是没法找到一个合适的决策边界来进行完美的划分

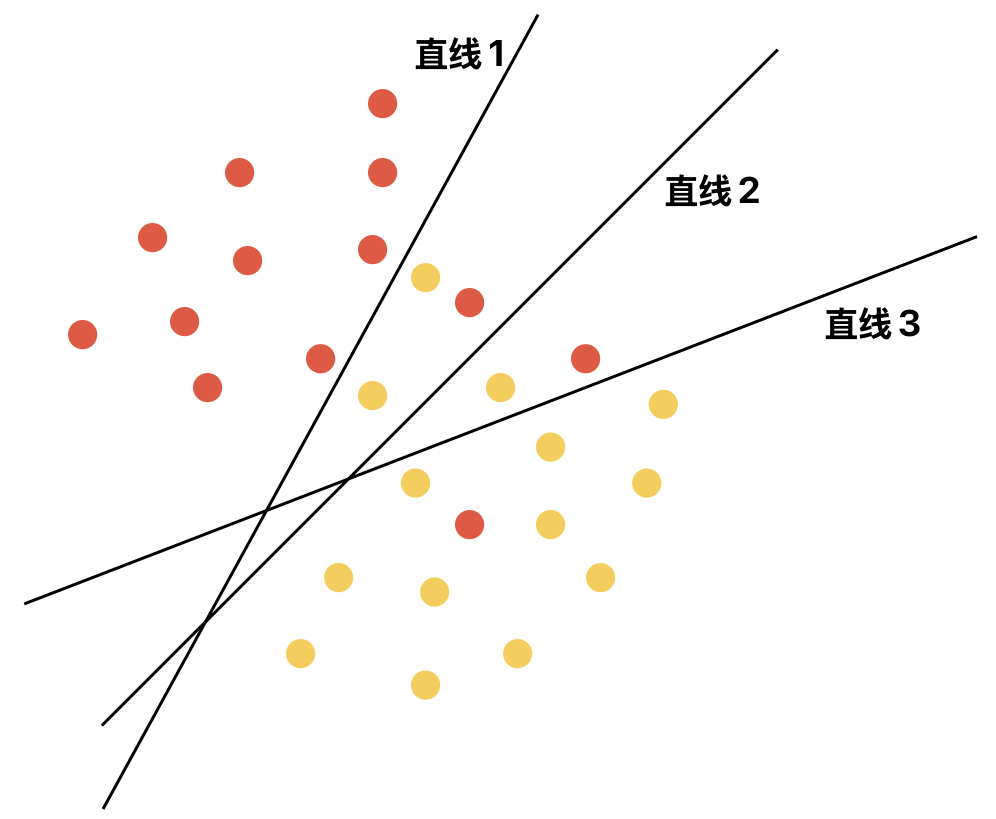
figure 3.png

为此SVM引入了Soft Margin软间隔，其可以允许少部分样本发生违规。具体地，不仅可以允许少部分样本位于在 决策边界与支持向量之间的间隔区域 中，甚至允许少部分样本被决策边界错误分类

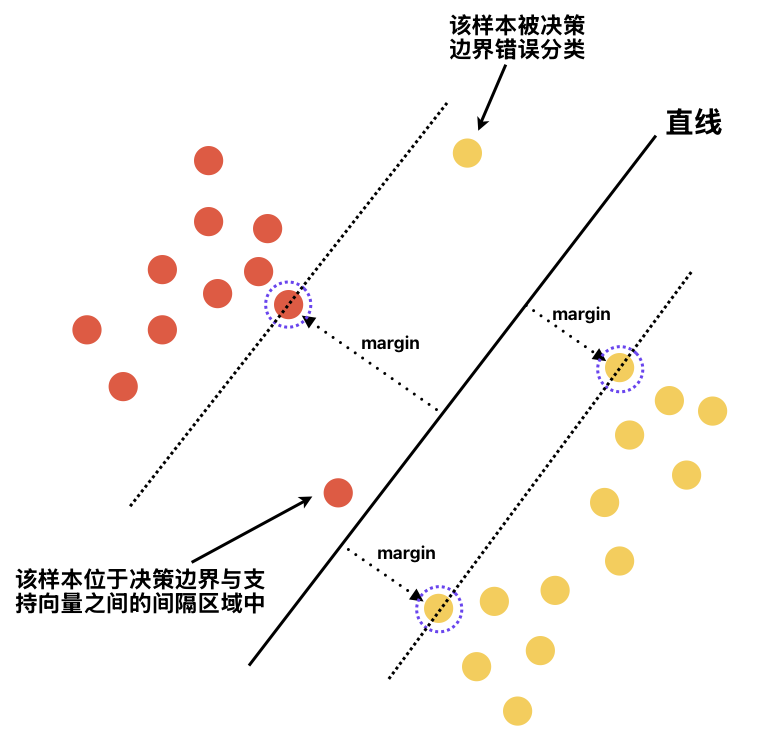
figure 4.png

为了实现软间隔，引入了超参数一一惩罚参数C。其用于衡量、控制对违规样本的惩罚强度

  • 惩罚参数C越大：说明对违规样本的惩罚强度越大。会导致模型倾向于选择减少违规样本（因为惩罚的力度很大）的决策边界。即：选择决策边界的目标是对分类错误的最小化。显然此时容易发生过拟合。因为模型学习了训练集中的噪音、异常值。特别地，当C趋于无穷大时，就退化为硬间隔SVM。因为其不允许任何样本出现分类错误
  • 惩罚参数C越小：说明对违规样本的惩罚强度越小。会导致模型倾向于容忍更多的违规样本（因为惩罚的力度很小）来选择间隔更大的决策边界。显然此时容易发生欠拟合。值得一提的是，惩罚参数C必须大于0。因为一旦为0，则会对违规样本没有任何惩罚。进而导致选择决策边界时就只保证间隔的最大，而完全不关心训练集是否分类正确。显然这样的模型是没有任何实际价值的

核函数

SVM的优势在于其不仅可以处理线性可分的样本，对于非线性可分的样本还可以通过核技巧进行处理。具体地，样本虽然在原始的低维空间是线性不可分的，但核函数可将样本映射到高维空间，使得样本在高维空间下线性可分。这样SVM即可在高维空间下找到一个线性的决策边界来划分样本。这里举一个具体的例子，帮忙理解为什么升维可以帮助实现数据的线性可分。假设在一个二维空间下，包含两种类别的样本。这两种类别的样本分布各自形成一个具有相同圆心的圆环

  • 红色点：属于类别A，其位于内圆环
  • 蓝色点：属于类别B，其位于外圆环

figure 5.png

显然，在原始的二维空间下，这两种类别的样本根本不可能通过线性决策边界（一条直线）进行完美的分离。但如果我们增加一个维度一一高度，其中每个样本的高度值为圆环的半径。则此时不难知道，在三维空间下，上述样本会呈现出下述特征：

  • 红色点：属于类别A，其位于内圆环。由于圆环半径较小，故其高度值较低
  • 蓝色点：属于类别B，其位于外圆环。由于圆环半径较大，故其高度值较高

此时，由于两种类别样本各自的高度值不同，我们在三维空间下就可以很容易找到这样一个的平面，使得所有蓝色点都在该平面的上方、所有红色点都在该平面的下方。即：对于这样一个二维空间下线性不可分的样本集，我们通过升维实现了其在三维空间下的线性可分

上述例子通过引入一个新的维度（高度），并显式映射、计算样本在新维度下的特征值（样本的高度值为圆环的半径）来帮助大家理解为什么升维可以实现在高维空间下的线性可分。而核函数的巧妙之处就在于：其隐式的实现样本从低维空间到高维空间的映射。这样一方面，避免了在高维空间下显式进行复杂的计算；另一方面，又达到了利用高维空间实现样本线性可分的目的。常见的核函数有：

  • 线性核：作为最简单的一种核函数，顾名思义其是一种线性核函数。其计算的依然是两个样本在原始特征空间中的内积，并没有进行升维。换言之，此时依然是在特征的原始维度空间中寻找决策边界。适用于样本集线性可分或近似线性可分的场景
  • 高斯核：作为最常用的非线性核函数，适用于样本集线性不可分的场景。其可将原始低维空间的样本隐式地映射到一个无限维的空间下。使得原本线性不可分的样本集在高维空间中变得线性可分

实践

这里通过SKlearn提供的SVM向量机来实现一个简单的二分类任务

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from matplotlib.lines import Line2D

# 构造分类标签为0的数据集
X_moons, y_moons = make_blobs(n_samples=200, centers=np.array([[0,0]]), random_state=69, cluster_std=0.8)
y_moons = np.zeros_like(y_moons)  

# 构造分类标签为1的数据集
X_blobs, y_blobs = make_blobs(n_samples=200, centers=np.array([[3,3]]), random_state=69, cluster_std=1)
y_blobs = np.ones_like(y_blobs)  

# 类别名称
label_names = ["Class #0", "Class #1"]

# 合并数据集
X = np.vstack((X_moons, X_blobs))
y = np.hstack((y_moons, y_blobs))

# 划分训练集、测试集，比例为7:3。固定random_state种子保证每次划分结果一样，可重复
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=69)

# 创建支持向量机分类器实例:核函数使用线性核、惩罚参数C为1
svm = SVC(kernel='linear', C=1)  

# 训练模型
svm.fit(X_train, y_train)

# 预测测试集
y_pred = svm.predict(X_test)

# 计算评估指标
report = classification_report(y_test, y_pred, target_names=label_names)
print("------------------------ 评估指标 ------------------------")
print(f"{report}")

# 创建一个包含两个子图的Figure, 其中子图的布局为1行2列
# 返回：一个Figure对象、一个包含子图轴Axes对象的数组
fig, axes = plt.subplots(1, 2)

# 计算输入样本在X轴、Y轴的边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
# 创建二维网格的x、y坐标
mesh_x, mesh_y = np.meshgrid(np.arange(x_min, x_max, 0.01), np.arange(y_min, y_max, 0.01))
# 网格点的x、y坐标
mesh_xy = np.hstack((mesh_x.ravel()[:, np.newaxis], mesh_y.ravel()[:, np.newaxis]))
# 计算每个网格点的预测结果, 并调整为网格的形状
mesh_z = svm.predict(mesh_xy)
mesh_z = mesh_z.reshape(mesh_x.shape)
# 绘制决策边界
axes[0].contourf(mesh_x, mesh_y, mesh_z, alpha=0.3, cmap="viridis")
axes[1].contourf(mesh_x, mesh_y, mesh_z, alpha=0.3, cmap="viridis")

# 可视化 训练集
axes[0].scatter(X_train[:, 0], X_train[:, 1], c=y_train, edgecolors='k', cmap='viridis')
# X、Y轴比例相等
axes[0].set_aspect('equal')
# 设置标题
axes[0].set_title('Train Set')

# 获取支持向量
support_vectors = svm.support_vectors_
# 绘制支持向量
axes[0].scatter(support_vectors[:, 0], support_vectors[:, 1], facecolors='none', edgecolors='r', s=100)

# 可视化 测试集
axes[1].scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolors='k', cmap='viridis')
# X、Y轴比例相等
axes[1].set_aspect('equal')
# 设置标题
axes[1].set_title('Test Set')

# 获取viridis颜色映射对象
viridis = plt.colormaps.get_cmap("viridis")

# 创建自定义图例
legend_elements = [
    # 深蓝色散点 表示 真实分类标签为0
    Line2D([],[], marker='o', markerfacecolor=viridis(0.0), markersize=8, markeredgecolor='k', color="none", label=label_names[0]),
    # 浅黄色散点 表示 真实分类标签为1
    Line2D([],[], marker='o', markerfacecolor=viridis(1.0), markersize=8, markeredgecolor='k', color="none", label=label_names[1])
]
# 添加图例
axes[1].legend(handles=legend_elements)
legend_elements.append(
    Line2D([],[], marker='o', markersize=8, markeredgecolor='r', color="none", label="Support Vector")
 )
axes[0].legend(handles=legend_elements)

# 自动调整子图的布局间距
plt.tight_layout()
# 设置Figure标题
fig.suptitle("SVM", fontweight='bold')
# 显示图形
plt.show()

输出结果如下：

1
2
3
4
5
6
7
8
9
------------------------ 评估指标 ------------------------
              precision    recall  f1-score   support

    Class #0       0.98      1.00      0.99        65
    Class #1       1.00      0.98      0.99        55

    accuracy                           0.99       120
   macro avg       0.99      0.99      0.99       120
weighted avg       0.99      0.99      0.99       120

分类效果如下

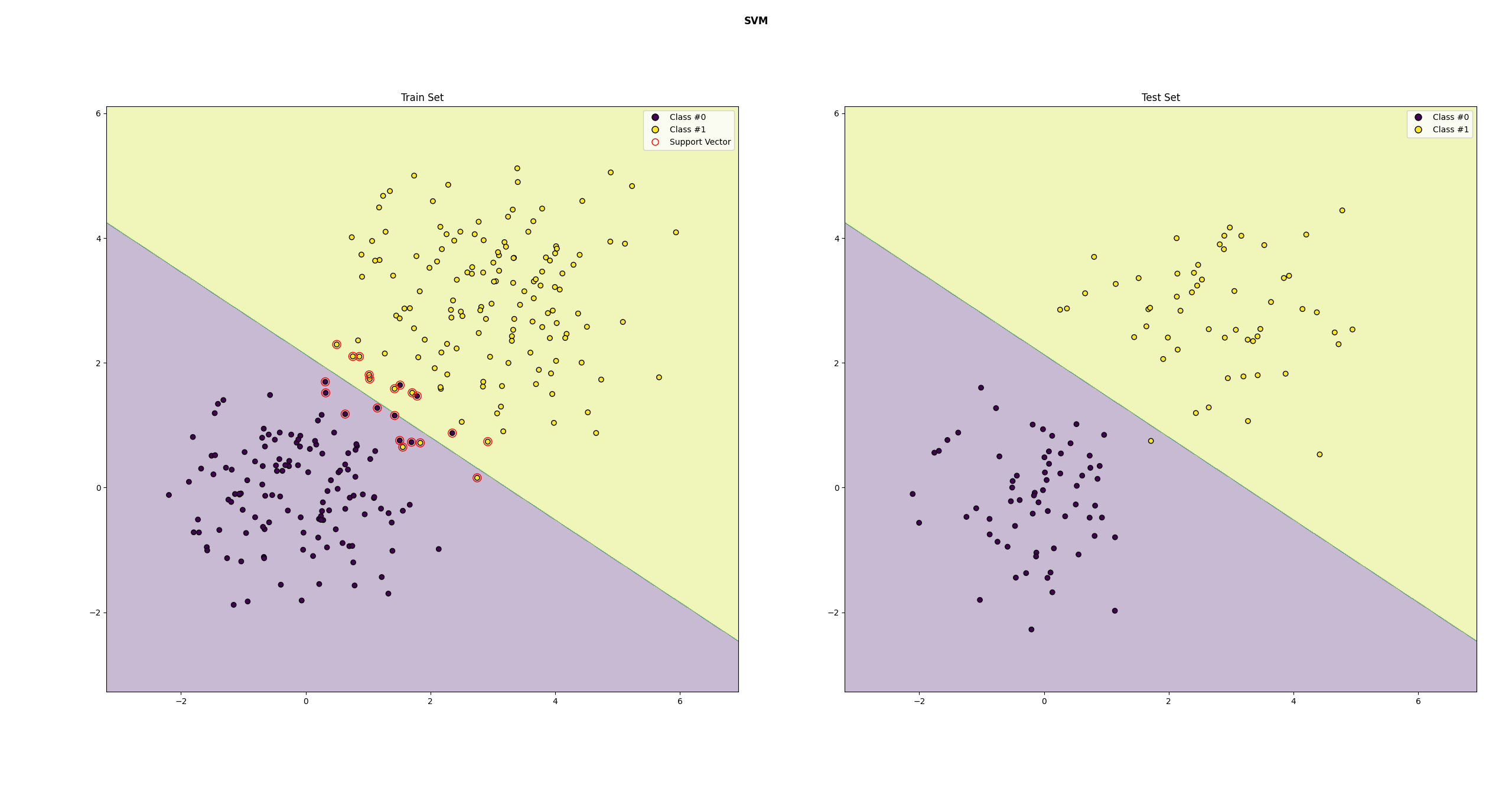
figure 6.png

特点

优点

  • 对于非线形可分的数据，可通过核技巧进行处理
  • 基于Soft Margin软间隔的SVM具有更强的泛化能力，对噪声、异常值具有较强的鲁棒性
  • 模型训练完成后，只需存储支持向量、决策边界的参数 即可进行预测。无需保留完整的训练集
  • 针对特征维度较大的场景，SVM算法也能保持较好的性能表现，而不像KNN、逻辑回归等算法容易发生维度灾难

缺点

  • 由于SVM在训练阶段的计算复杂度非常高。故对于大规模训练集而言，训练耗时较长
  • 模型的超参数（惩罚参数C、核函数类型等）调优困难
  • 可解释性较差。因为相比于其他的线性分类器（例如：逻辑回归等），SVM的决策边界是由少数的支持向量来决定的。特别是在使用了非线性的核函数后，高维空间下的线性决策边界还原到原始的低维空间下会变得比较复杂，难以直观理解

参考文献

  • 机器学习 周志华著
  • 机器学习公式详解 谢文睿、秦州著
  • 图解机器学习和深度学习入门 山口达辉、松田洋之著
推荐文章
请我喝杯咖啡捏～
  • 本文作者： Aaron Zhu
  • 本文链接： https://xyzghio.xyz/SVM/
  • 版权声明： 本博客所有文章除特别声明外，均采用 BY-NC-ND 许可协议。转载请注明出处！

欢迎关注我的微信公众号：青灯抽丝