HashSet的底层是使用一种称为哈希表的数据结构，值得一提的是，在Java中，HashSet内部是使用HashMap来存储元素的(将整个元素作为key)

概述

内部结构

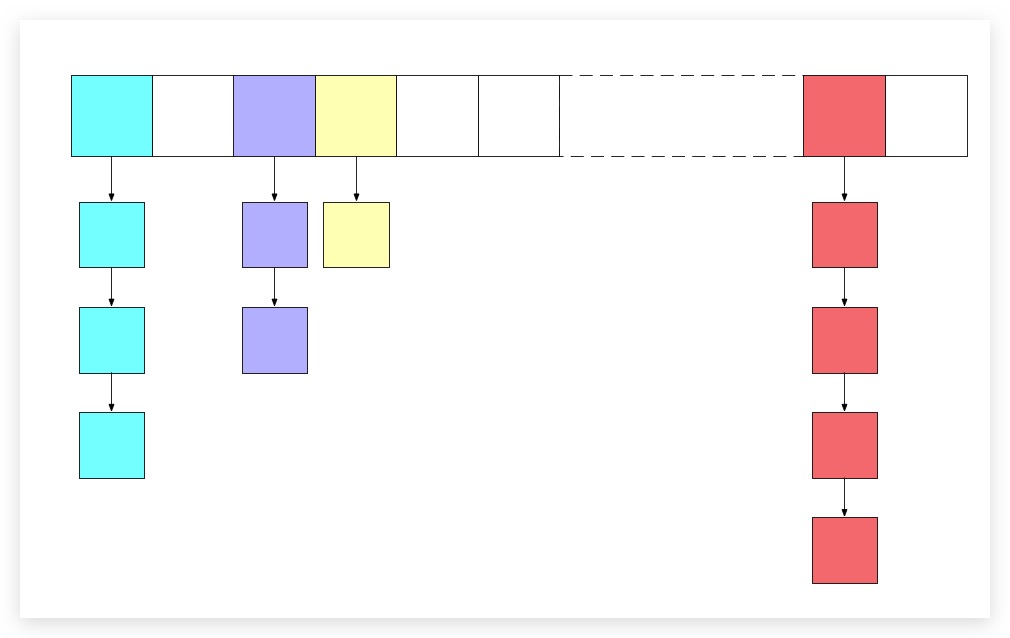
JDK 7

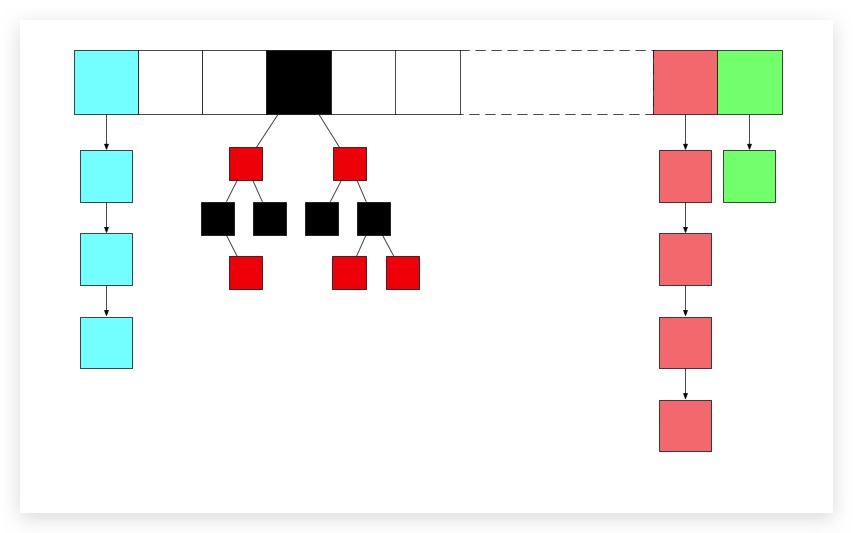
JDK 8

在JDK 7版本中，哈希表是采用数组+链表实现。每个链表被称为桶(bucket)。插入对象时，需要确定其应在表中的位置，首先需要计算该对象的哈希值，然后与桶的总数取余(其实不是很准确，后文将详述)，则余数即为对象在哈希表中的位置索引。如果该桶为空(如上图白色桶所示)，则可将该对象直接插入相应索引的桶中；如果该桶已经被占满（如上图彩色桶所示），则需要将该对象与该桶中的所有对象进行比较，看看是否已经存在该对象，如果全部比较后均不存在，则将其添加到该桶中
在JDK 8版本中，对于哈希表的实现做了一些改进，通过数组+链表+红黑树实现。当某个桶经常发生哈希冲突时，该链表长度将会变的非常长，下一次新对象将必须依次比较该桶中的所有对象，耗费大量时间降低性能。为此当桶中对象数量超过8个时，在JDK 8 中会将该链表转换为红黑树(如上图黑色桶所示)进行存储。此举将大大减少新对象在该桶的比较次数，提高性能

初始桶数 initial capacity

如果可以预估插入到整个哈希表中的元素总数，则可以指定桶数的初始值。在Java中，如果构造时不指定初始值，则使用默认值16；如果指定初始值，由于Java使用的桶数均为2的幂，则将使用一个比指定初始值最近大的2的幂(即，指定初值为18，实际将使用32进行初始化;指定初值为32，实际将使用32进行初始化;)

Note: 有些研究人员认为：虽然没有充足的证据，但是推荐将桶数设置为一个质数

装填因子 load factor

一方面，不是总能预估哈希表中的元素总数；另一方面，即使当时可以预估，但是很多时候由于未来情况的变化，致使哈希表中的元素总数大幅增加，使得哈希表性能开始下降。此时就需要进行再哈希，创建一个桶数更多的新哈希表，将原有哈希表中的所有元素重新插入到新哈希表中，然后丢弃原有的哈希表。这里通过计算 被占满桶数/桶数，将其与装填因子load factor进行比较。当前者比值达到装填因子设定值时，该哈希表将使用一个比当前哈希表桶数大一倍（由于Java使用的桶数均为2的幂）的新哈希表自动进行再哈希。在Java中装填因子默认值为0.75，即哈希表中超过75%的桶已经填入元素时将进行再哈希

源码分析

tableSizeFor方法

前文提到，如果在HashSet构造器中提供桶数的初始值时，JDK会判断该值是否为2的幂，如果是，则使用提供的初值；否则，将其自动对齐为下一个最近的2幂，并使用该值进行初始化。其在构造器中通过调用 tableSizeFor 方法完成上述2幂的对齐操作

现对JDK 11的源码实现进行分析

 // The maximum capacity, used if a higher value is implicitly specified by either of the constructors with arguments. MUST be a power of two <= 1<<30.
static final int MAXIMUM_CAPACITY = 1 << 30;
// Returns a power of two size for the given target capacity.
static final int tableSizeFor(int cap) {
    int n = -1 >>> Integer.numberOfLeadingZeros(cap - 1);
    return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

这里首先对于Integer.numberOfLeadingZeros方法的做简要介绍，该方法返回参数二进制(计算机存储的二进制为补码)的前导零的个数：

// 负数补码的符号位均为1，故其前导零的数量均为0
Integer.numberOfLeadingZeros(-12)   ==>> 返回 0
Integer.numberOfLeadingZeros(-1)    ==>> 返回 0
// 正数补码即为原码
Integer.numberOfLeadingZeros(0)     ==>> 返回 32
Integer.numberOfLeadingZeros(1)     ==>> 返回 31

源码中的形参cap即为我们向构造器中指定的初值桶数，这里分为两种情况进行讨论：

cap为2幂：令其二进制有x位有效数字，其中第x位为1，第x-1位～第1位为0；cap-1的二进制则变为x-1位有效数字，第x-1位～第1位均为1；

从上图易知Cap-1的前导零的个数为33-x。-1的二进制(补码)，第32位～第1位全为1，将其无符号右移33-X后即为n：

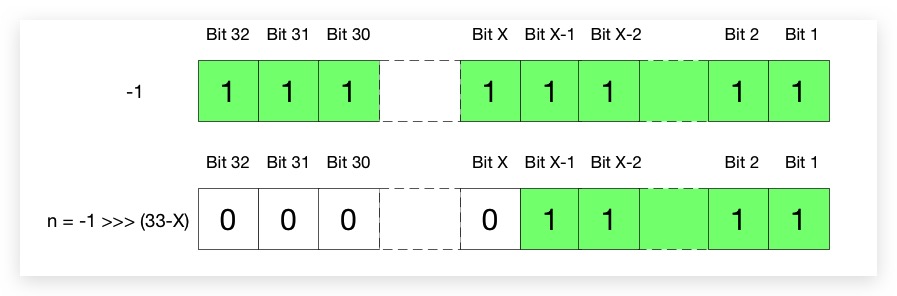
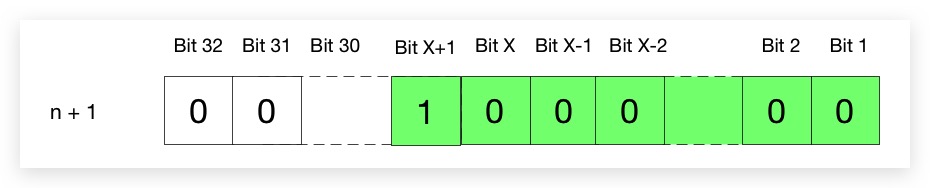
最后，进行n+1操作，从下图可以看出，则所得结果和前文形参Cap一致，且为2幂

cap不为2幂：令其二进制有x位有效数字，其中第x位为1，则第x-1位～第1位中必存在一个1，故cap-1的二进制依然为x位有效数字，易知第x位为1；

从上图易知Cap-1的前导零的个数为32-x。-1的二进制(补码)，第32位～第1位全为1，将其无符号右移32-X后即为n：

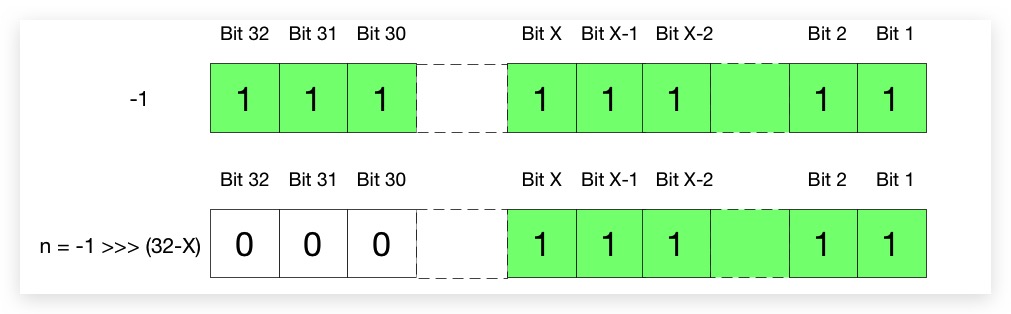
最后，进行n+1操作，从下图可以看出，则所得结果即为距离前文形参Cap最近的下一个2幂

桶位置索引的计算

前文提到，关于元素在链表数组中的位置计算，是用元素的哈希值与桶总数取余得到。其实这种表述并不准确。现根据JDK 11给出准确的解释：

下述代码中通过位运算完成元素哈希值hash与桶总数n取余后用于确定桶位置索引i，十分巧妙且效率高。n表示总桶数,hash可以暂时理解就是元素的哈希值。前文已经说明，在Java中，由于其总桶数n均为2幂，其二进制应该为100…00，则n-1后，恰好变为11…11，则正好为n余数的低位掩码，此时再将n-1与hash做位与计算后，其结果正好就是 hash%n

1	i = (n - 1) & hash;

但是上述方法的缺陷也很明显，即指只考虑了hash值的低x位(余数掩码位)，这样对于那些高位有差异，而在余数掩码位一致的元素而言，将大大增加其哈希冲突的可能性。为此，Java设计了一个如下的扰动函数:

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

将元素的哈希值h 与哈希值h无符号右移16位后进行XOR异或操作得到一个新的hash值，然后再用新哈希值hash与总桶数n求余来确定最后元素所存放的桶的位置索引
对元素哈希值h进行扰动计算，其通过简单高效的位运算实现将原哈希值h中的高位和低位信息进行融合，尽可能提高了低位信息的随机性，以降低发生冲突的可能性

rehash时新位置的计算

在JDK 11 中当需要进行rehash将调用resize()进行自动扩容，其中关于扩容后新位置的计算很巧妙，现结合扩容前后的图解进行分析说明，如前文所述，图中hash均为原哈希值经过扰动后的值

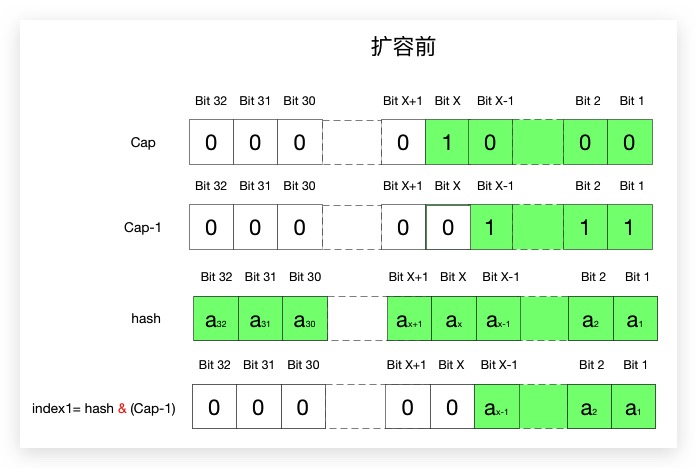
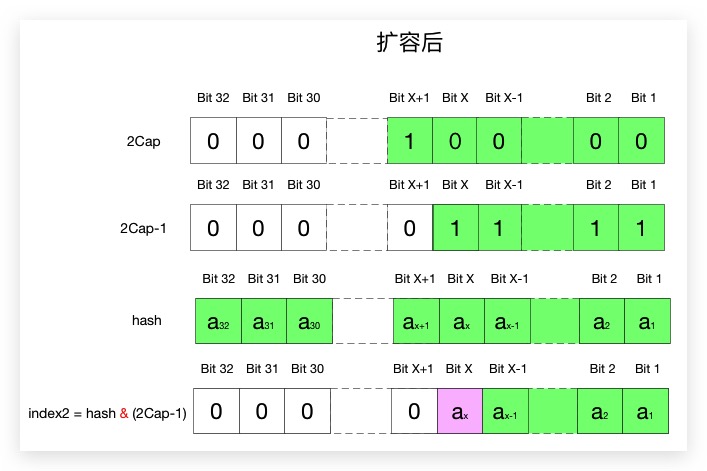
通过上图，可以看出发生扩容后余数掩码位比扩容前多了一位(Java中，扩容为当前容量的下一个2幂)，所以：

如果hash的第X位为0，即 $a_x = 0$ , 则 $index2 = index1$ ，扩容后该元素的位置保持不变；
如果hash的第X位为1，即 $a_x = 1$ , 则为 $index2 = index1 + cap$ ，扩容后的位置该元素的位置为原位置和原容量大小之和

所以在resize的源码中可以看到其通过(cap & hash)实现判断hash的第X位是否为1：

与结果为0，则第X位为0；
与结果为1，则第X位为1；

扩容后新位置计算的伪代码如下:

if( cap & hash )
{
    newIndex = oldIndex + oldCap;
}
else
{
    newIndex = oldIndex;
}

HashSet 方法

HashSet 提供了多种情况下的构造函数:

public HashSet();   // 构造一个空哈希表
public HashSet(int initialCapacity);    // 构造一个指定桶数的空哈希表
// 构造一个指定桶数，指定装填因子的空哈希表    
public HashSet(int initialCapacity, float loadFactor);  

// 构造一个哈希表，并将集合c 中的所有元素添加到该哈希表中
public HashSet(Collection<? extends E> c);

特点

底层使用哈希表实现
元素不可重复
排列无序（准确说，应该是其不保证有序。迭代器在遍历HashSet时，大多情况下是无序的，但也可能由于巧合，使其输出恰好为有序，这也是允许的。所以你的程序不应该依赖这个巧合的有序情况，而应该按照无序这种普适的情况进行处理）
存取速度快
线程不安全

xyZGHio

Java集合: HashSet 哈希集

概述