浅谈SkipList跳表

跳表SkipList由William Pugh发表提出，是一种对插入、查找、删除操作可以实现平均时间复杂度为对数时间的数据结构。相比较传统的平衡树(AVL Tree、Red-Black Tree)而言，其最大的优点在于原理、实现都非常简单、方便。广泛应用于Redis、Kafka、LevelDB中

基本原理

楔子

对于一个有序链表而言，如下所示。我们在进行插入、删除、查找时，需要从头逐个遍历整个链表。其时间复杂度为线性时间。那有没有办法提高呢？答案自然是有的

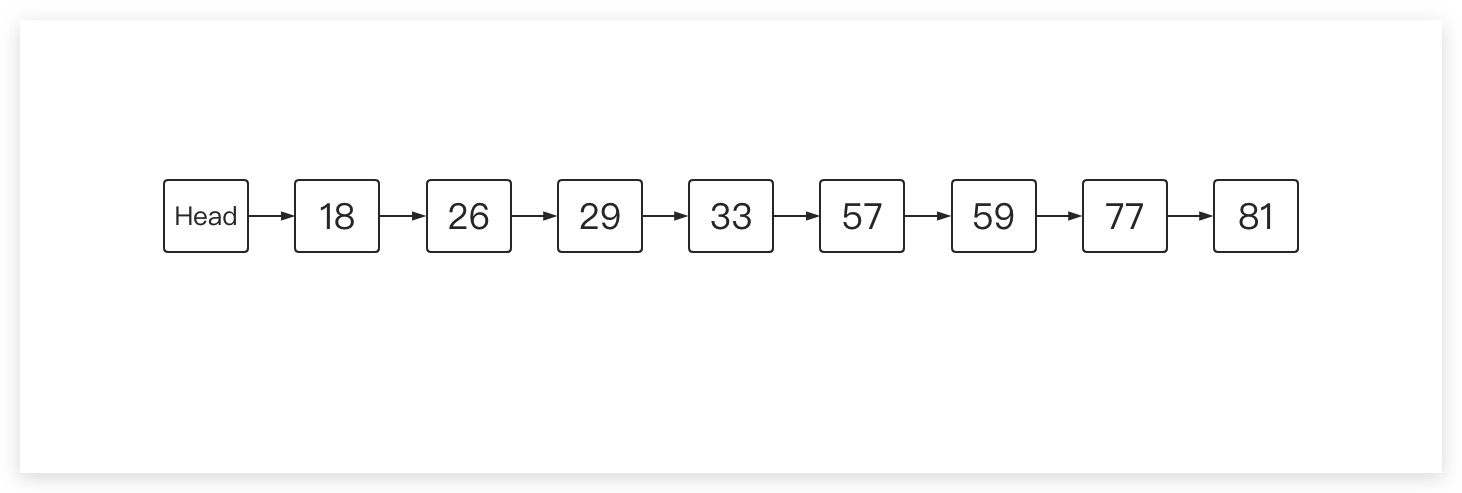
我们在原有序链表之上建立索引，从下图可以看出，我们加入了第1、2层。其中第1层形成的链表只是由原链表中的部分元素所构成，第2层同理。至此可以看出跳表是一个多层链表的结构，除第0层链表包含所有元素，其余各层链表只是由部分元素所构成。并且每一层链表均是有序的，这样即可实现在遍历过程中快速跳过很多不符合要求的元素

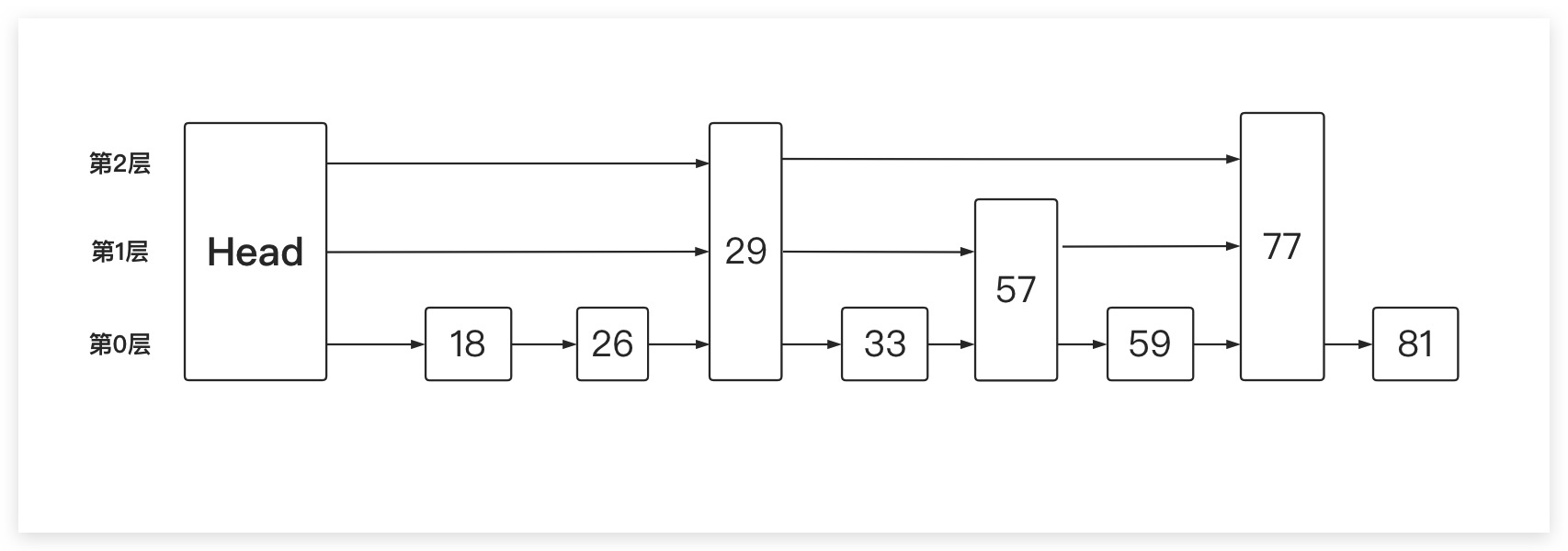
具体地，我们对这样一个跳表进行查询操作：判断59是否存在于其中。则我们首先从第2层的链表开始遍历。当遍历到29时，由于该节点在第2层链表的下一个节点为77，即29是本层链表最后一个小于59的节点。此时将会进入下一层继续遍历，即从第1层链表的值为29的节点继续在本层进行遍历。然后不断重复上述过程。如果最终在第0层也没找到指定值的节点。则说明该元素不存在于跳表中，否则即存在。当然这里显然是存在的

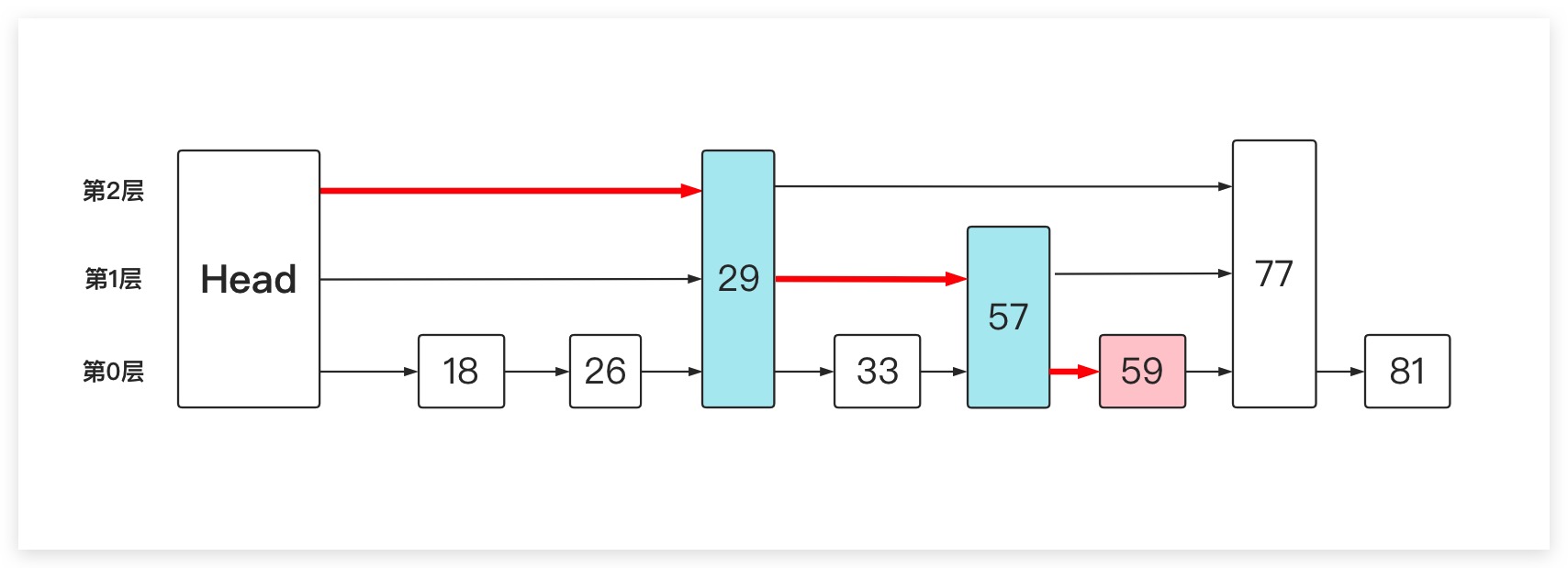
至此让大家对跳表的用途、原理有了一个基本的认识。现在我们来看看具体怎么实现一个跳表。因为上面的跳表是对一个已有的有序链表添加索引形成的，而实际跳表的建立是一个动态的过程。即每次在添加、删除一个元素过程中，我们都需要建立、维护跳表的整个索引

添加

在向上述跳表添加一个元素时，我们需要先确定该节点的层数。这里我们假设添加的新节点值为34、层数为3(从第0层开始计数)。由下图可知，跳表的原层数为2(通过值为29、77的节点可知)。则对于由于添加元素导致的新增层数而言，即第3层。我们只需让该层链表的表头直接指向新节点即可。而对于第2层而言，我们只需找到该层最后一个小于34的节点，即值为29的节点。然后将新节点插入到其后面。第1层同理。当到了第0层时，此时该层最后一个小于34的节点，是值为33的节点。同样将新节点插入到其后面

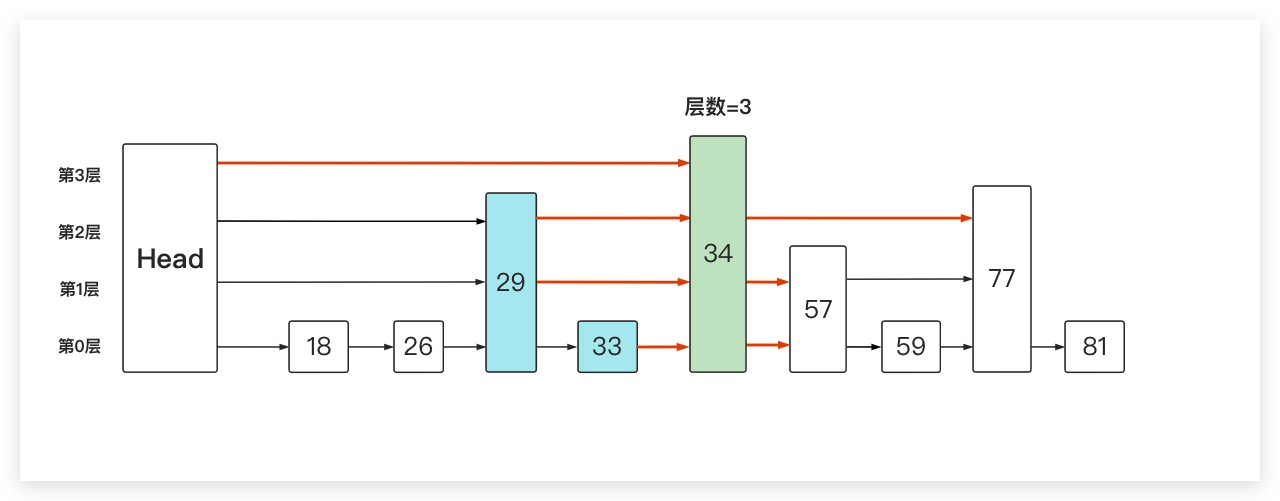
其实不难看出，在我们添加一个新节点的过程中。需要从上往下进行添加。其中是否将节点添加到第i层的链表当中，取决于新节点的层数。例如在刚刚的添加过程中，如果新节点的层数为1。则只需从第1层的链表开始添加，而第2层的链表则保持不变。如下所示

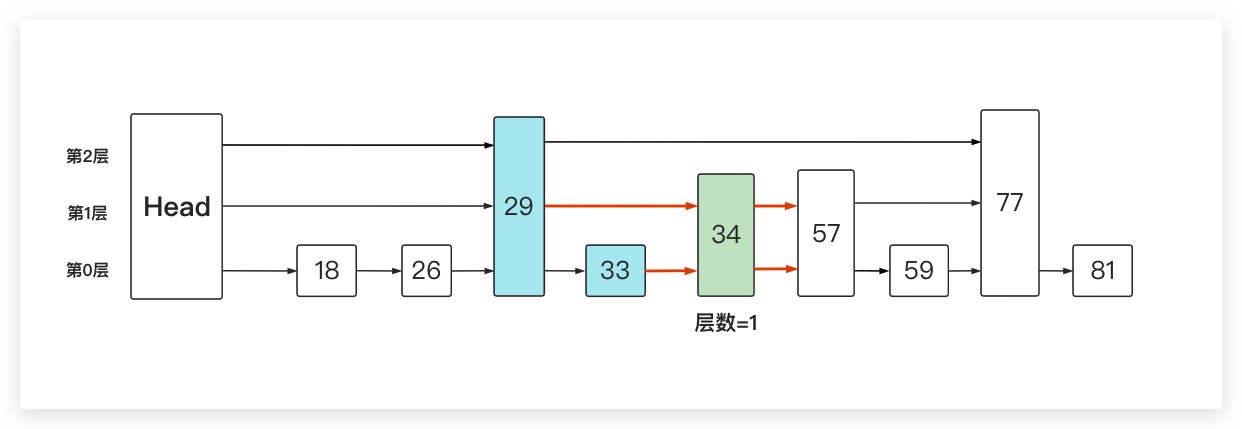
这里对新节点层数如何确定进行阐述。为了实现跳表操作平均时间复杂度为对数时间，我们需要让每一层链表的节点数量尽量控制在是下一层链表节点数的1/2。换言之，每一个处于第i层链表的节点都有1/2的概率出现在第i+1层的链表中。此时，我们就可以通过生成随机数的方式来确定新节点的层数了。但一般我们都会限制跳表的最大层数，以防层数过高带来的性能退化

查找

在跳表中查找一个元素，其实上面已经介绍过思路了。从上层链表开始遍历，当发现链表后继节点的值超过搜索值。则说明本层链表查找已经结束了。我们需要进入下层链表继续遍历。直到查找到指定元素为止。当在第0层链表依然未找到，则说明该元素不存在于跳表当中

删除

对跳表进行删除操作也很简单。依然还是从上到下逐层遍历跳表、依次进行删除。具体地，当在本层跳表找到指定元素后，进行链表的节点删除即可。然后进入下一层链表，重复上述操作。直到第0层处理完毕为止

实现

学习过程中要善于理论联系实际。故在介绍完基本原理后，我们通过Java来实现一个跳表。这里以LeetCode的第1206题——设计跳表为例

不使用任何库函数，设计一个跳表
在本题中，你的设计应该要包含这些函数：

• bool search(int target) : 返回target是否存在于跳表中
• void add(int num): 插入一个元素到跳表
• bool erase(int num): 在跳表中删除一个值，如果num不存在，直接返回false. 如果存在多个num ，删除其中任意一个即可

Note: 跳表中可能存在多个相同的值，你的代码需要处理这种情况

这里给出Java下的实现，具体如下所示

/**
 * 跳表
 */
class Skiplist {
    /**
     * 跳表的最大层数
     */
    private static final int MAX_LEVEL = 15;

    /**
     * 跳表第i层的元素出现在第i+1层的概率
     */
    private static final double p = 0.5;

    /**
     * 表头
     */
    private Node head;

    /**
     * 跳表层数, 从0开始计数
     */
    private int currentLevel;

    public Skiplist() {
        this.head = new Node(null, MAX_LEVEL);
        this.currentLevel = 0;
    }

    /**
     * 添加一个元素到跳表中
     * @param num
     */
    public void add(int num) {
        // 随机生成层数
        int newLevel = getRandomLevel();
        // 创建节点实例
        Node newNode = new Node(num, newLevel);
        Node node = head;
        for (int level = currentLevel; level>=0; level--) {
            if( level > newLevel ) {
                continue;
            }
            // 找到欲插入num的前一个节点
            node = getLastLessThanNum(node, num, level);
            // 将节点实例插入到当前层的链表中
            Node temp = node.next[level];
            node.next[level] = newNode;
            newNode.next[level] = temp;
        }

        // 新节点层数 超过 跳表原层数
        if( newLevel>currentLevel ) {
            // 新增层数链表的表头直接 指向 新节点 即可 
            for(int level = newLevel; level>currentLevel; level--) {
                head.next[level] = newNode;
            }
            // 更新跳表层数
            currentLevel = newLevel;
        }
    }

    /**
     * 判断当前元素是否存在于跳表中
     * @param num
     * @return
     */
    public boolean search(int num) {
        Node node = head;
        for(int level=currentLevel; level>=0; level--) {
            node = getLastLessThanNum(node, num, level);
            // 在跳表当前层找到指定元素
            if( node.next[level]!=null && node.next[level].val.equals(num) ) {
                return true;
            }
        }

        return false;
    }

    /**
     * 从跳表中删除一个元素
     * @param num
     * @return 如果num不存在, 直接返回false; 如果存在多个num 删除其中任意一个即可
     */
    public boolean erase(int num) {
        // 删除成功标记
        boolean flag = false;
        Node node = head;
        for (int level=currentLevel; level>=0; level--) {
            node = getLastLessThanNum(node, num, level);
            // 在跳表当前层找到指定元素
            if( node.next[level]!=null && node.next[level].val.equals(num) ) {
                flag = true;
                // 链表的节点删除: 将node 指向 指定元素的后继节点
                node.next[level] = node.next[level].next[level];
            }
        }

        // 重新计算跳表的层数
        for(int level=0; level<=MAX_LEVEL; level++) {
            if(head.next[level] == null) {
                currentLevel = level-1;
                break;
            }
        }

        return flag;
    }

    /**
     * 获取一个随机层数, 范围: [0, 15]
     * @return
     */
    private int getRandomLevel() {
        int level = 0;
        while (Math.random()<p && level<MAX_LEVEL) {
            level++;
        }
        return level;
    }

    /**
     * 在跳表指定层的链表中寻找最后一个小于num的节点
     * @param node 链表
     * @param num
     * @param level 跳表层数
     * @return
     */
    private Node getLastLessThanNum(Node node, Integer num, int level) {
        Node current = node;
        while ( current.next[level]!=null && current.next[level].val<num ) {
            current = current.next[level];
        }
        return current;
    }

    /**
     * 跳表节点
     */
    private static class Node {
        private Integer val;

        private Node[] next;

        public Node(Integer val, int size) {
            this.val = val;
            this.next = new Node[size+1];
        }
    }
}

参考文献

1. Redis设计与实现 黄健宏著