浅谈单调栈

本文介绍一种基于栈的特殊数据结构——单调栈

基本原理

所谓单调栈，其本质上依然是一个满足FILO先进后出的栈。只不过对于单调栈而言，其栈内的元素按照某种排序规则可以保证单调递增或单调递减。如果后续准备入栈的元素破坏了栈的单调性，则先需要进行弹栈操作直到满足单调性才可以对新元素进行入栈。这里补充说明下，之所以采用某种排序规则的说法。是因为很多时候我们不是把元素直接进行入栈的。而是选择把它在集合容器中的位置索引进行入栈的。显然此时我们在操作栈时，比较的是位置索引所指向的元素。具体地，单调栈可细分为单调递增栈、单调递减栈

• 单调递增栈：栈内的元素按照某种排序规则可以保证从栈顶到栈底是单调递增的
• 单调递减栈：栈内的元素按照某种排序规则可以保证从栈顶到栈底是单调递减的

对于单调栈而言，其解决的是一类问题：即寻找元素左侧或右侧第一个比它大或小的元素

寻找元素左侧第一个比它大的元素

对于一个一维数组而言，对数组每一个元素来说，我们期望寻找元素左侧第一个比它大的元素时。即可以采用单调递增栈进行解决

1. 对一维数组按从左到右的顺序进行遍历
2. 如果栈顶所对应的元素 不大于 当前元素, 就一直弹栈。直到满足单调性要求为止
3. 此时对于当前元素而言，栈顶所对应的元素 即为 左侧第一个比其大的元素
4. 然后再将当前元素入栈
5. 重复Step 2 - Step 4，直到一维数组遍历完为止

寻找元素左侧第一个比它小的元素

对于一个一维数组而言，对数组每一个元素来说，我们期望寻找元素左侧第一个比它小的元素时。即可以采用单调递减栈进行解决

1. 对一维数组按从左到右的顺序进行遍历
2. 如果栈顶所对应的元素 不小于 当前元素, 就一直弹栈。直到满足单调性要求为止
3. 此时对于当前元素而言，栈顶所对应的元素 即为 左侧第一个比其小的元素
4. 然后再将当前元素入栈
5. 重复Step 2 - Step 4，直到一维数组遍历完为止

寻找元素右侧第一个比它大的元素

此场景本质上还是寻找第一个比它大的元素，故依然使用单调递增栈进行解决。只不过我们需要找的是元素右侧而已，故只需将一维数组从右到左遍历即可

寻找元素右侧第一个比它小的元素

此场景本质上还是寻找第一个比它小的元素，故依然使用单调递减栈进行解决。只不过我们需要找的是元素右侧而已，故只需将一维数组从右到左遍历即可

实践

单调递增栈

学习过程中要善于理论联系实际。故在介绍完单调递增栈的基本原理后，现在我们来进行实践。这里以LeetCode的第739题——每日温度为例

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指在第 i 天之后，才会有更高的温度。如果气温在这之后都不会升高，请在该位置用 0 来代替

示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]

提示：
1 <= temperatures.length <= 105
30 <= temperatures[i] <= 100

本题的本质是在数组中寻找元素右侧第一个比它大的元素。故我们采用单调递增栈，并对数组按从右到左遍历即可。Java实现如下所示

/**
 * 单调递增栈
 */
public class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int size = temperatures.length;
        int[] res = new int[size];
        // 单调递增栈
        Deque<Integer> stack = new LinkedList<>();

        for(int i=size-1; i>=0; i--) {
            // 当前温度
            int curTem = temperatures[i];
            // 如果栈顶所对应的温度 不大于 当前温度, 就一直弹栈
            while ( !stack.isEmpty() && temperatures[stack.peek()] <= curTem ) {
                stack.poll();
            }
            // 此时栈顶的位置索引 即为 右侧第一个比当前温度高的元素位置索引
            res[i] = stack.isEmpty() ? 0 : stack.peek()-i;
            // 当前温度的位置索引入栈
            stack.push(i);
        }

        return res;
    }
}

单调递减栈

学习过程中要善于理论联系实际。故在介绍完单调递减栈的基本原理后，现在我们来进行实践。这里以LeetCode的第84题——柱状图中最大的矩形为例

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积

示例 1:

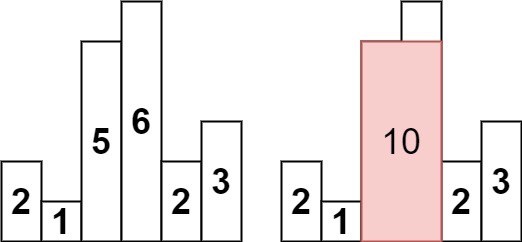
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

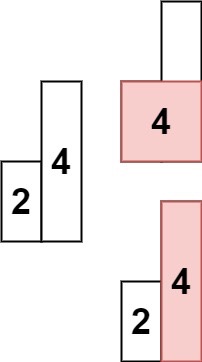
输入： heights = [2,4]
输出： 4

提示：
1 <= heights.length <=105
0 <= heights[i] <= 104

对于本题而言，问题的关键在于对于一个以当前元素为高度的矩形，如何确定该矩形的左、右边界。即我们需要分别在元素的左侧、右侧找到第一个比它大的元素。故这里采用单调递减栈，先对数组按从左到右遍历确定左边界，然后对数组按从右到左遍历确定右边界。Java实现如下所示

/**
 * 单调递减栈
 */
class Solution {
    public int largestRectangleArea(int[] heights) {
        int maxArea = 0;
        int size = heights.length;

        // 当前元素 左侧第一个比它小的元素位置索引
        int[] leftBoard = new int[size];
        // 当前元素 右侧第一个比它小的元素位置索引
        int[] rightBoard = new int[size];

        // 单调递减栈
        Deque<Integer> stack = new LinkedList<>();
        // 计算左边界
        for (int i=0; i<size; i++) {
            // 当前元素
            int current = heights[i];
            // 如果栈顶所对应的元素 不小于 当前元素, 就一直弹栈
            while ( !stack.isEmpty() && heights[stack.peek()] >= current ) {
                stack.pop();
            }
            // 此时栈顶的位置索引 即为 左侧第一个比当前元素小的元素位置索引
            leftBoard[i] = stack.isEmpty() ? -1 : stack.peek();
            // 当前元素的位置索引入栈
            stack.push(i);
        }

        stack.clear();
        // 计算右边界
        for (int i=size-1; i>=0; i--) {
            // 当前元素
            int current = heights[i];
            // 如果栈顶所对应的元素 不小于 当前元素, 就一直弹栈
            while ( !stack.isEmpty() && heights[stack.peek()] >= current ) {
                stack.pop();
            }
            // 此时栈顶的位置索引 即为 右侧第一个比当前元素小的元素位置索引
            rightBoard[i] = stack.isEmpty() ? size : stack.peek();
            // 当前元素的位置索引入栈
            stack.push(i);
        }

        for (int i=0; i<size; i++) {
            // 计算以当前元素为高度的矩形的面积
            int tempArea = (rightBoard[i]-leftBoard[i]-1) * heights[i];
            if( tempArea > maxArea ) {
                maxArea = tempArea;
            }
        }

        return maxArea;
    }
}