Levenshtein Distance莱文斯坦距离，属于编辑距离的一种。由苏联数学家Vladimir Levenshtein于1965年提出

基本原理

两个字符串之间的Levenshtein Distance莱文斯坦距离指的是将一个字符串变为另一个字符串需要进行编辑操作最少的次数。其中，允许的编辑操作有以下三种。不难看出其可用于衡量两个字符串之间的差异，故被广泛应用于拼写纠错检查、DNA分析、语音识别等领域

替换：将一个字符替换成另一个字符
插入：插入一个字符
删除：删除一个字符

对于两个字符串A、B而言，字符串A的前i个字符和字符串B的前j个字符的莱文斯坦距离符合如下公式

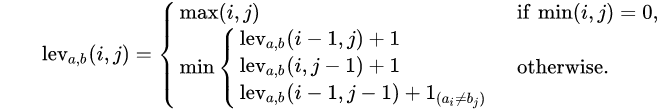
其中：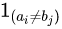

是一个Indicator Function指示函数，当字符串a的第i个字符和字符串b的第j个字符不同时，其值为1；否则为0

公式解释

至少存在一个字符串为空串

若字符串A是一个长度为0的空字符串时，则其变为长度为n的字符串B。只需对字符串A进行n次插入操作即可；同理，若字符串A是一个长度为n的字符串时，则其变为长度为0的空字符串B。则只需对字符串A进行n次删除操作即可。故在上述公式中，可将这两种情况统一为：当两个字符串的长度最小值为0时，则说明有一个字符串为空串。则这二者之间的莱文斯坦距离为两个字符串长度的最大值

两个字符串均不为空串

当两个字符串均不为空串时，这里假设字符串A为horse、字符串B为ros进行举例分析。由于上述三种类型的操作不会改变字符串中各字符的相对顺序，故我们可以这样进行思考。每次仅对字符串A末尾进行操作，即只考虑字符串A的前i个字符和字符串B的前j个字符的莱文斯坦距离。其中。这里的i、j均为从1开始计数。则字符串A的前5个字符和字符串B的前3个字符的莱文斯坦距离lev(5,3)，就是最终我们所求的字符串A、字符串B之间的莱文斯坦距离

插入

假设我们把 horse 变为 ro 的莱文斯坦距离记为u，即：

1 2	# 字符串A的前5个字符和字符串B的前2个字符的莱文斯坦距离为 u lev(5,2) = u

则 horse 期望变为 ros，其所需的编辑次数不会超过 u+1。因为 horse 只需先经过u次编辑操作变为 ro，然后在尾部插入s字符即可变为 ros

删除

假设我们把 hors 变为 ros 的莱文斯坦距离记为v，即：

1 2	# 字符串A的前4个字符和字符串B的前3个字符的莱文斯坦距离为 v lev(4,3) = v

则 horse 期望变为 ros，其所需的编辑次数不会超过 v+1。因为 horse 只需先进行一次删除操作变为 hors，再经过v次编辑操作即可变为 ros

替换

假设我们把 hors 变为 ro 的莱文斯坦距离记为w，即

1 2	# 字符串A的前4个字符和字符串B的前2个字符的莱文斯坦距离为 w lev(4,2) = v

则 horse 期望变为 ros，其所需的编辑次数不会超过 w+1。因为 horse 只经过w次编辑操作即可变为 roe，然后通过一次替换操作，将尾部的e字符替换为s字符即可

至此，在这个例子中不难看出，horse、ros的莱文斯坦距离满足如下的递推公式

1
2
3

lev(horse, ros) = lev(5,3) 
                = min( lev(5,2)+1, lev(4，3)+1, lev(4,2)+1 )
                = min(u+1, v+1, w+1)

特别地，这里对通过替换途径实现的方式做一定的说明。如果某字符串A的第i个字符与某字符串B的第j个字符完全相同，则其所需的编辑次数肯定不会超过 lev(i-1, j-1)。因为无需进行替换

通过上面的分析过程，我们其实不难看出。如果期望字符串A的前i个字符与字符串B的前j个字符完全相同。可以有如下三种途径操作方式进行实现。而最终的莱文斯坦距离就是下面三种实现方式中次数最小的一个

在字符串A的前i个字符与字符串B的前j-1个字符完全相同的基础上，进行一次插入操作
在字符串A的前i-1个字符与字符串B的前j个字符完全相同的基础上，进行一次删除操作
在字符串A的前i-1个字符与字符串B的前j-1个字符完全相同的基础上，如果字符串A的第i个字符与字符串B的第j个字符不同，则需要进行一次替换操作；如果字符串A的第i个字符与字符串B的第j个字符相同，则无需进行任何操作

实践

学习过程中要善于理论联系实际。故在介绍完该算法后，这里以LeetCode的第72题——编辑距离为例进行实践。本题的本质实际上就是计算Levenshtein Distance莱文斯坦距离

给你两个单词 word1 和 word2，请返回将 word1 转换成 word2 所使用的最少操作数。你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符

示例 1：
输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

示例 2：
输入：word1 = “intention”, word2 = “execution”
输出：5
解释：
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

Note：
0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

通过上面对该算法的分析、解释，实际不难通过Java进行编程

class Solution {
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        if( m*n == 0 ) {
            return Math.max(m, n);
        }

        int[][] lev = new int[m+1][n+1];

        // 字符串word1从空串 变为 字符串word2 前j个字符 的莱文斯坦距离
        for (int j=0; j<n+1; j++) {
            lev[0][j] = j;
        }
        // 字符串word1从前i个字符 变为 空串 的莱文斯坦距离
        for (int i=0; i<m+1; i++) {
            lev[i][0] = i;
        }

        for (int i=1; i<m+1; i++) {
            for (int j=1; j<n+1; j++) {
                // 在 字符串A的前i个字符 与 字符串B的前j-1个字符 完全相同的基础上, 进行一次插入操作
                int countByInsert = lev[i][j-1] + 1;
                // 在 字符串A的前i-1个字符 与 字符串B的前j个字符 完全相同的基础上, 进行一次删除操作
                int countByDel = lev[i-1][j] + 1;
                // 在 字符串A的前i-1个字符 与 字符串B的前j-1个字符 完全相同的基础上, 进行一次替换操作
                int countByReplace =  word1.charAt(i-1)==word2.charAt(j-1) ? lev[i-1][j-1] : lev[i-1][j-1]+1;
                // 计算 字符串A的前i个字符 与 字符串B的前j个字符 的莱文斯坦距离
                lev[i][j] = min( countByInsert, countByDel, countByReplace );
            }
        }

        return lev[m][n];
    }

    /**
     * 计算三个数中的最小值
     * @param a
     * @param b
     * @param c
     * @return
     */
    private int min(int a, int b, int c) {
        int temp = Math.min(a,b);
        int res= Math.min(temp, c);
        return res;
    }
}

xyZGHio

浅谈Levenshtein Distance莱文斯坦距离算法

基本原理

公式解释

至少存在一个字符串为空串

两个字符串均不为空串

实践