树状数组或二元索引树(BIT, Binary Indexed Tree)作为一种高效计算数组前缀和的数据结构,又以其发明者被命名为Fenwick Tree

楔子
给定一个数组a:2、1、7、5
在进行单点更新操作时,得益于索引下标其时间复杂度为O(1)。例如:a[2] = 996
而如果需要计算该数组的前缀和,则需要进行遍历。其时间复杂度为O(n)。例如:sum[2]=a[0]+a[1]+a[2]=2+1+7=10
那如果换个思路,我们将原数组转换为相应的前缀和数组s:2、3、10、15
此时期望获取原数组a的前缀和,则可直接通过前缀和数组的索引下标进行获取,其时间复杂度为O(1)。例如:s[2]=10
但在进行单点更新时,由于我们需要维护前缀和数组s,故需要遍历该数组、并将增量更新到相应元素上。其时间复杂度为O(n)。例如,将原数组索引为1的元素减小2。则:
s[1]=3-2=1
s[2]=10-2=8
s[3]=15-2=13
那如何能够同时兼顾单点更新与前缀和这两种操作的在时间上的效率呢?答案就是下面所要介绍的Fenwick Tree树状数组。其能够实现在单点更新、前缀和操作上的对数时间复杂度
lowbit函数
而在介绍Fenwick Tree树状数组之前,我们先来介绍一个前置知识。如何计算非负整数n在二进制表示下最低位1及其后面的0所构成的数值,为后续行文方便记为lowbit函数。举个例子,172在二进制下可以表示为10101100,则我们期望lowbit(127) = 0b100 = 4
而lowbit函数的实现则可通过位运算,具体如下所示。其中,方式1与方式2本质上是等价的。因为负数在计算机中是用补码表示的,即对正数进行取反再加1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
public class LowBit {
public static void main(String[] args) {
Integer num1 = 172;
Integer result1 = num1 & (~num1+1);
Integer result2 = num1 & -num1;
System.out.println("num1: " + Integer.toBinaryString(num1) + " -->> " + num1);
System.out.println("num2: " + Integer.toBinaryString(result1) + " -->> " + result1);
System.out.println("num3: " + Integer.toBinaryString(result2) + " -->> " + result2);
}
}
|
测试结果如下所示,符合预期
Fenwick Tree树状数组
基本原理
假设存在这样的一个数组:1,3,2,1,0,6,8,4,9,1,4。我们按照同一层两两向上归并求和的思路建立Fenwick Tree树状数组,如下所示。例如第一层的1、3合并得到第二层的4;然后每一列只保留最顶层的元素,例如第2列4、3只保留上面的4。这里为了便于观察,在建立Fenwick Tree树状数组过程中,将需要丢弃的中间计算结果标记红底,将需要保留下来的元素标记为绿底
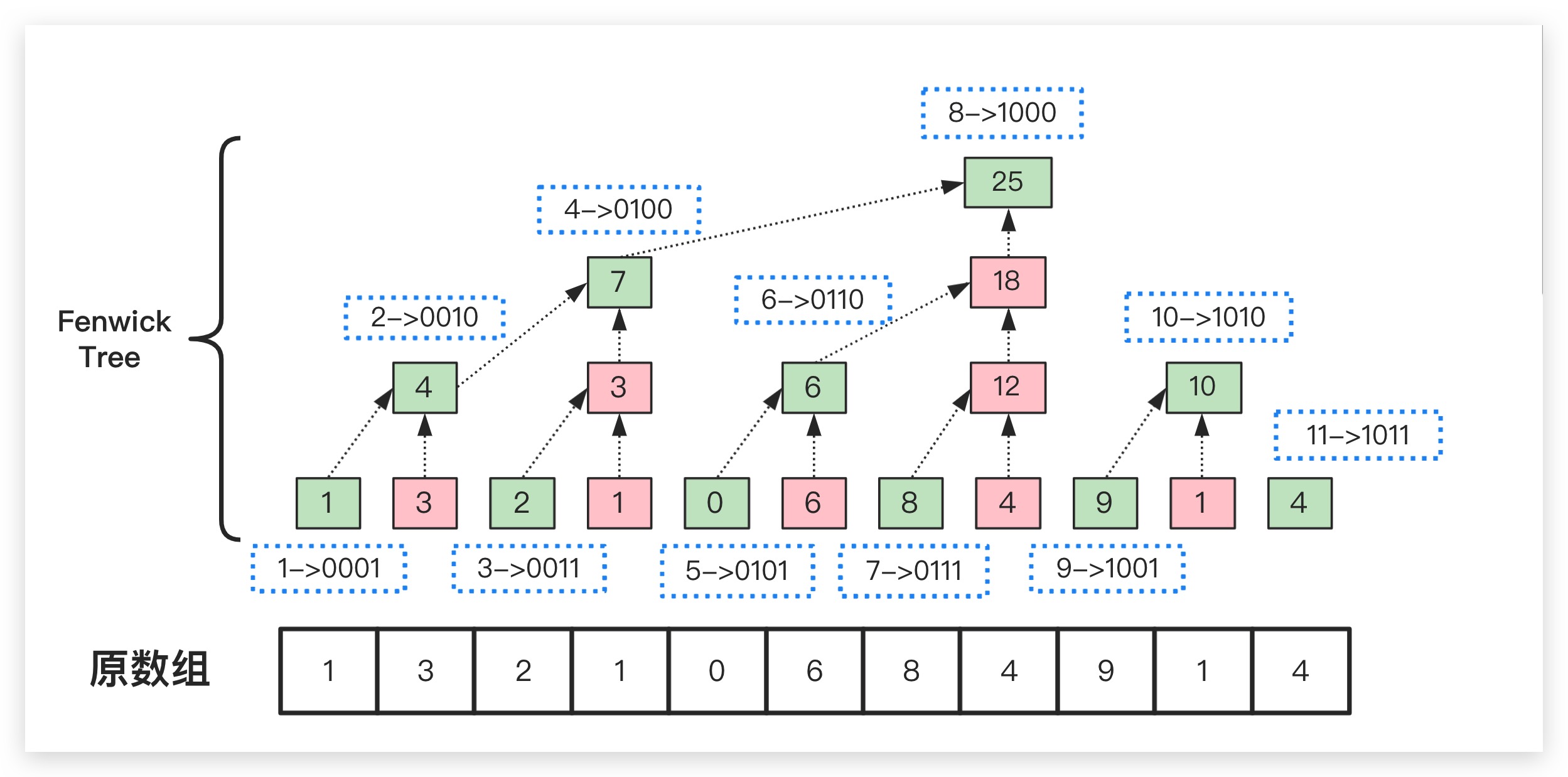
则最终树状数组的如下所示。可以看到其逻辑上虽然是一棵树,但物理上却可以通过数组来进行表示。这也是树状数组名称的由来
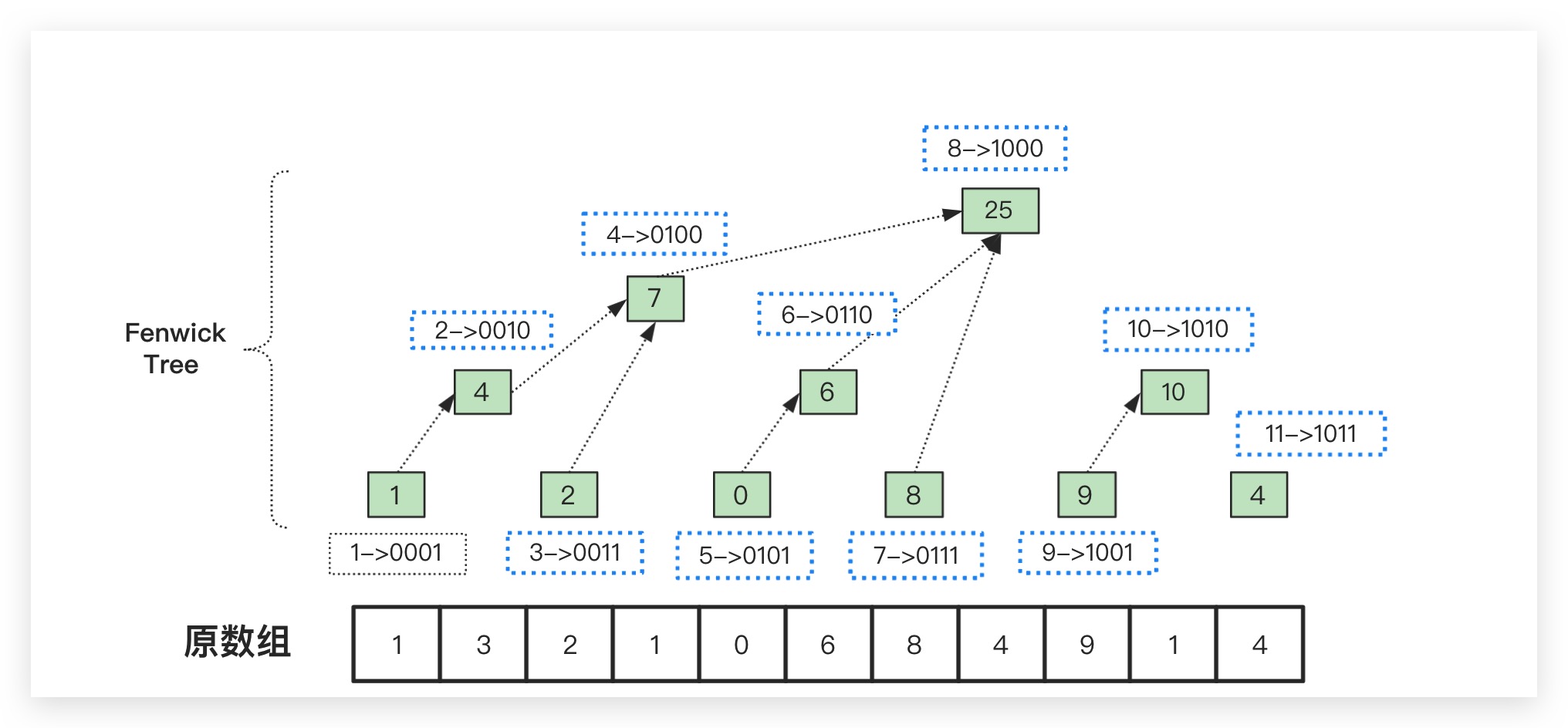
对于树状数组bit而言,我们规定其索引下标从1开始。则树状数组中的元素值如下
1
2
3
4
5
| bit[1]=1, bit[2]=4, bit[3]=2
bit[4]=7, bit[5]=0, bit[6]=6
bit[7]=8, bit[8]=25, bit[9]=9
bit[10]=10
bit[11]=4
|
从上不难看出,对于树状数组中的元素而言,其是原数组a中部分元素的和。需要再次提醒:原数组的索引是从0开始的,而树状数组的元素则是从1位置开始存储的。所以原数组的元素索引要比相应的树状数组的元素索引小1
1
2
3
4
5
6
| bit[1] = a[0] = 1
bit[2] = a[0]+a[1] = 1+3 = 4
bit[3] = a[2] = 2
bit[4] = a[0]+a[1]+a[2]+a[3] = 1+3+2+1 = 7
bit[5] = a[4] = 0
...
|
前面提到逻辑上数组bit是一颗树,故bit数组的元素值是其各子节点的元素值、及其所对应的原数组元素之和。例如
1
2
3
4
5
| bit[2] = bit[1]+a[1] = 1+3 = 4
bit[4] = bit[3]+bit[2]+a[3] = 2+4+1 = 7
bit[8] = bit[7]+bit[6]+bit[4]+a[7] = 8+6+7+4 = 25
bit[10] = bit[9]+a[9] = 9+1 = 10
...
|
单点更新
如果期望对原数组a[1]进行修改,则首先需要更新树状数组相应的元素,即bit[2]。与此同时还需要更新所有的父节点:bit[4]、bit[8]。同理,修改a[4]需要更新树状数组bit[5]、bit[6]、bit[8];修改a[9]需要更新树状数组bit[10]
现在问题就来了,如何找到树状数组bit某个节点的父节点呢?这里以bit[5]及其父节点bit[6]、bit[8]的索引为例,将其转换为二进制
1
2
3
| 5 = 0101
6 = 0110 = 0101 + 1
8 = 1000 = 0110 + 10
|
从上不难看出,子节点与父节点索引的计算方式为
1
| parentIndex = childIndex + lowbit(childIndex)
|
例如5的二进制为0101,其lowbit(5)=lowbit(0b0101)=1。则索引为5的树状节点,其父节点的索引为 5+1 = 6
前缀和
从上图不难可以看出:
1
2
3
| bit[4] = a[0]+a[1]+a[2]+a[3] = 1+3+2+1 = 7
bit[6] = a[4]+a[5] = 0+6 = 6
bit[7] = a[6] = 8
|
那如果期望计算原数组的前缀和。例如a[0]~a[6]的和,则只需计算bit[7]、bit[6]、bit[4]三者之和。现在问题就来了,如何获取树状数组的索引下标呢?首先第一个下标肯定是原数组a[6]元素所对应树状数组的索引,即bit[7]。而剩余的6、4怎么得来呢?其实很简单,我们将其转换为二进制
1
2
3
| 7 = 0111
6 = 0110 = 0111 - 1
4 = 0100 = 0110 - 10
|
其实不难看出,当前节点与下一个节点索引的计算方式为
1
| nextIndex = currentIndex - lowbit(currentIndex)
|
例如7的二进制为0111,其lowbit(7)=lowbit(0b0111)=1。则下一个节点索引为 7-1=6
同理6的二进制为0110,其lowbit(6)=lowbit(0b0110)=0b10=2。则下一个节点索引为 6-2=4
同理4的二进制为0100,其lowbit(4)=lowbit(0b0100)=0b100=4。则下一个节点索引为 4-4=0。但由于树状数组的索引是从1开始的,故索引0是无效的
Java实现
至此可以看到通过Fenwick Tree树状数组,可以高效地进行单点修改、前缀和。而利用前缀和则可进一步实现区间查询、单点查询。基于Java的实现如下所示
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
|
public class FenwickTree1 {
private int[] array;
private int[] bit;
public FenwickTree1(int[] array) {
this.array = new int[ array.length ];
this.bit = new int[ array.length+1 ];
for(int i=0; i<array.length; i++) {
update(i, array[i]);
}
}
public void update(int index, int num) {
int delta = num - array[index];
array[index] = num;
int bitIndex = index+1;
while ( bitIndex < bit.length ) {
bit[bitIndex] += delta;
bitIndex = bitIndex + lowBit(bitIndex);
}
}
public int getPrefixSum(int index) {
int sum = 0;
int bitIndex = index+1;
while (bitIndex>0) {
sum += bit[ bitIndex ];
bitIndex = bitIndex - lowBit(bitIndex);
}
return sum;
}
public int getRangeSum(int startIndex, int endIndex) {
int prefixUSum2 = getPrefixSum(endIndex);
if( startIndex==0 ) {
return prefixUSum2;
}
int prefixUSum1 = getPrefixSum(startIndex-1);
int rangSum = prefixUSum2 - prefixUSum1;
return rangSum;
}
public int getElement(int index) {
return getRangeSum(index, index);
}
private int lowBit(int n) {
return n & -n;
}
}
|
拓展
区间修改、单点查询
所谓区间修改是指对指定区间范围内的每一个元素均增加指定的增量。前面提到Fenwick Tree树状数组支持单点修改,那进行区间修改自然也是可以的。直接将区间修改转换为若干次的单点修改。但此时时间复杂度就为线性对数时间了。那有没有办法将区间修改的时间复杂度降到对数级别呢,答案自然是可以的
这里引入差分数组d,用于计算原数组的差分结果。可以看到对原数组[L,R]区间增加num,反映在差分数组d上,只需对差分数组d进行两次单点修改即可。具体地,对d[L]增加num、d[R+1]减少num即可
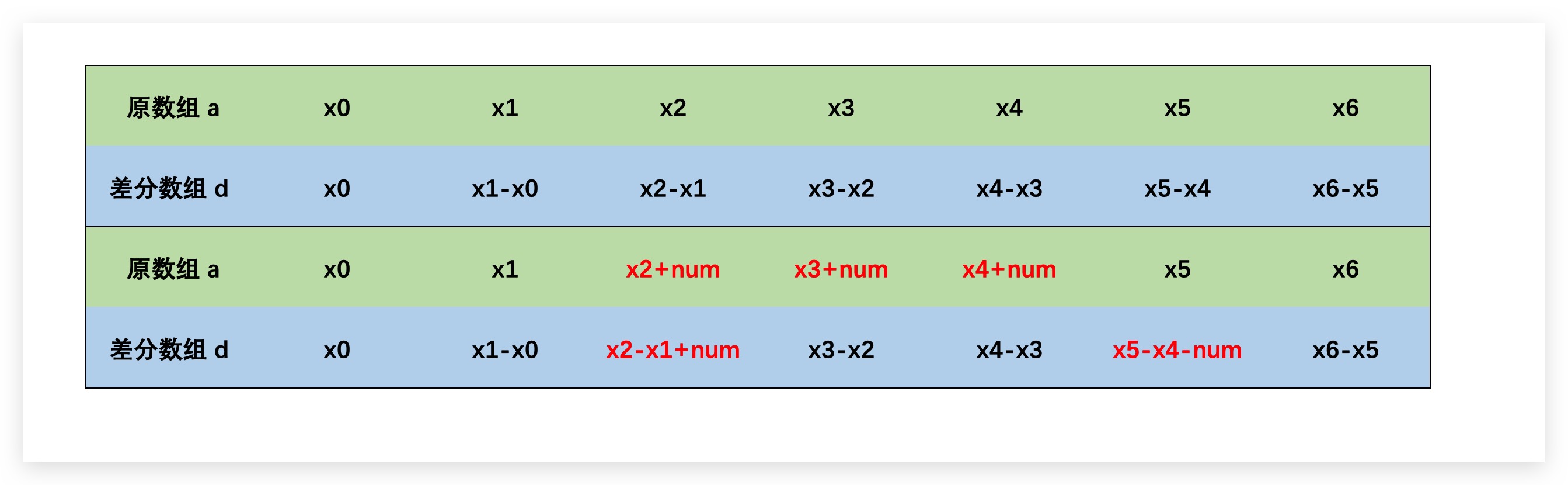
而如果期望对原数组进行单点查询,则只需计算差分数组的前缀和即可。例如:
1
2
3
4
5
6
7
| a[3] = d[0] + d[1] + d[2] + d[3]
= x0+(x1-x0)+(x2-x1+num)+(x3-x2)
= x3 + num
a[5] = d[0] + d[1] + d[2] + d[3] + d[4] + d[5]
= x0+(x1-x0)+(x2-x1+num)+(x3-x2)+(x4-x3)+(x5-x4-num)
= x5
|
换言之,如果期望进行区间修改、单点查询。只需先将原数组转换为差分数组,再对差分数组建立Fenwick Tree树状数组即可。基于Java的实现如下所示
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
|
public class FenwickTree2 {
private int[] array;
private int[] delta;
private int[] bit;
public FenwickTree2(int[] array) {
this.array = array;
delta = new int[ array.length ];
for(int i=0; i<array.length; i++) {
if ( i==0 ) {
delta[0] = array[0];
} else {
delta[i] = array[i] - array[i-1];
}
}
bit = new int[ delta.length+1 ];
for(int i=0; i<delta.length; i++) {
update(i, delta[i]);
}
}
public void updateRange(int startIndex, int endIndex, int num) {
update(startIndex, num);
if( endIndex < delta.length-1 ) {
update(endIndex+1, -num);
}
}
public int getElement(int index) {
int element = 0;
int bitIndex = index+1;
while (bitIndex>0) {
element += bit[ bitIndex ];
bitIndex = bitIndex - lowBit(bitIndex);
}
return element;
}
private void update(int index, int num) {
int bitIndex = index+1;
while ( bitIndex < bit.length ) {
bit[bitIndex] += num;
bitIndex = bitIndex + lowBit(bitIndex);
}
}
private int lowBit(int n) {
return n & -n;
}
}
|
区间修改、前缀和、区间查询
如前文所述,原数组的区间修改可借助于差分数组进行实现

结合上图上文易知
1
2
3
4
5
| a[0] = d[0]
a[1] = d[0]+d[1]
a[2] = d[0]+d[1]+d[2]
a[3] = d[0]+d[1]+d[2]+d[3]
...
|
那如何实现原数组的前缀和呢?比如计算a[0]~a[3]之和,则可知
1
2
| sum = a[0]+a[1]+a[2]+a[3]
= 4*d[0] + 3*d[1] + 2*d[2] + d[3]
|
但事实上这个计算非常不便,我们对sum进行可视化。具体地,将差分元素d[x]表示为:长为元素值d[x]、宽为1的矩形,如下图所示。可以看到sum值其实就是绿色部分的面积
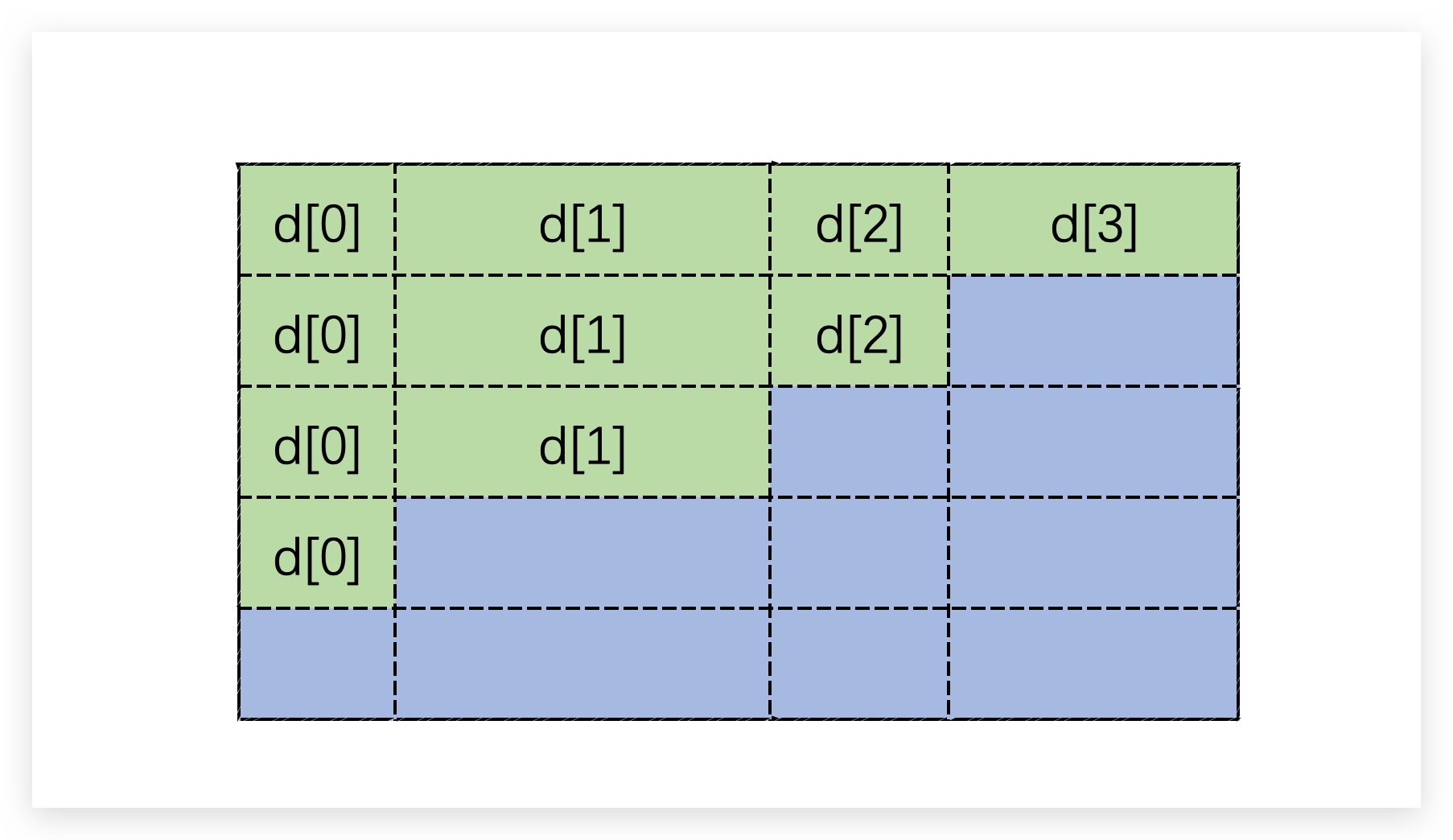
既然直接计算绿色部分的面积不便,我们转换个思路。用外部大矩形的面积减去蓝色部分的面积即可

至此可以发现,前半部分实际上就是差分数组的前缀和;而对于后半部分,则可先建立一个元素值为(i+1)*d[i]的辅助数组,然后通过计算该辅助数组的前缀和进行实现。即:
1
2
|
原数组的前缀和 = (i+2) * 差分数组的前缀和 - 辅助数组的前缀和
|
既然计算前缀和已经实现,则可进一步地进行区间查询。这里给出Java下的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
|
public class FenwickTree3 {
private int[] array;
private int[] delta;
private int[] bit1;
private int[] temp;
private int[] bit2;
public FenwickTree3(int[] array) {
this.array = array;
delta = new int[ array.length ];
for(int i=0; i<array.length; i++) {
if ( i==0 ) {
delta[0] = array[0];
} else {
delta[i] = array[i] - array[i-1];
}
}
temp = new int[ delta.length ];
for(int i=0; i<delta.length; i++) {
temp[i] = (i+1) * delta[i];
}
bit1 = new int[ delta.length+1 ];
for(int i=0; i<delta.length; i++) {
update(i, delta[i], bit1);
}
bit2 = new int[ temp.length+1 ];
for(int i=0; i<temp.length; i++) {
update(i, temp[i], bit2);
}
}
public void updateRange(int startIndex, int endIndex, int num) {
update(startIndex, num, bit1);
if( endIndex < delta.length-1 ) {
update(endIndex+1, -num, bit1);
}
update(startIndex, (startIndex+1)*num, bit2);
if( endIndex < temp.length-1 ) {
update(endIndex+1, -(endIndex+2)*num, bit2);
}
}
public int getPrefixSum(int index) {
int deltaSum = 0;
int bit1Index = index+1;
while (bit1Index>0) {
deltaSum += bit1[ bit1Index ];
bit1Index = bit1Index - lowBit(bit1Index);
}
int tempSum = 0;
int bit2Index = index+1;
while (bit2Index>0) {
tempSum += bit2[ bit2Index ];
bit2Index = bit2Index - lowBit(bit2Index);
}
int result = (index+2) * deltaSum - tempSum;
return result;
}
public int getRangeSum(int startIndex, int endIndex) {
int prefixUSum2 = getPrefixSum(endIndex);
if( startIndex==0 ) {
return prefixUSum2;
}
int prefixUSum1 = getPrefixSum(startIndex-1);
int rangSum = prefixUSum2 - prefixUSum1;
return rangSum;
}
private void update(int index, int num, int[] bit) {
int bitIndex = index+1;
while ( bitIndex < bit.length ) {
bit[bitIndex] += num;
bitIndex = bitIndex + lowBit(bitIndex);
}
}
private int lowBit(int n) {
return n & -n;
}
}
|
应用
剑指Offer(第2版): 51. 数组中的逆序对
这里以经典例题为例展开介绍:LeetCode 的剑指Offer(第2版)题单中的第51题——数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数
示例 1:
输入:[7,5,6,4]
输出:5
对于本题而言最朴素的思路就是暴力遍历数组进行统计,但此举的时间复杂度数平方级别,显然不可接受
现在假设数组a为:2、3、9、7、6。我们依次遍历该数组统计重复元素出现的次数,并将统计结果保存到数组c中。其中索引为元素的值,值为次数。当准备遍历原数组的a[3]元素7时,统计结果数组c则如下所示
1
2
3
|
index -->> 2 3 6 7 9
count -->> 1 1 0 0 1
|
可以看到此时c[0]到c[7]之和为2。换句话说,对于原数组的第4个元素7而言,其与前面的3个元素依次比较,存在2个顺序对:(2,7)、(3,7)。则逆序对的数量为:3 - 2 = 1
同理,当准备遍历原数组的a[4]元素6时,统计结果数组c则如下所示。可以看到此时c[0]到c[6]之和为2。换句话说,对于原数组的第5个元素6而言,其与前面的4个元素依次比较,存在2个顺序对:(2,6)、(3,6)。则逆序对的数量为:4 - 2 = 2
1
2
3
|
index -->> 2 3 6 7 9
count -->> 1 1 0 1 1
|
最终对于数组a而言,其逆序对的数量共计为3。不难看出我们只需在遍历原数组过程中,计算统计结果数组c的前缀和即可。而计算统计结果数组c的前缀和则可通过Fenwick Tree树状数组来提高效率
但其实这里中还有一个小问题需要进行处理。前面提到统计结果数组的索引是源自原数组的元素值。比如假设原数组为:2、996、3。则统计数组c需要长度为997的数组空间,但实际上只会使用c[2]、c[3]、c[996]这三个元素位置。特别是如果原数组中存在一个非常大的数,显然这样会造成内存空间的极大浪费,且内存空间的利用率非常低。故我们需要对原数组的元素值进行离散化处理。就本题而言,我们需要的是元素之间的相对关系而非绝对值。一个非常简单的处理思路就是对原数组的N个元素进行去重、排序,用排序的顺序代替原来的元素值。这样就可将无限空间的元素值映射到1~N的排名范围内,这样统计数组c就只需长度为N+1的数组空间
例如原数组:112、996、203。排序后为:112、203、996,即112排名第1、203排名第2、996排名第3。故原数组离散化的结果即为:1、3、2。至此本题的思路、解法就完全清晰明了了,具体实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
class Solution {
private Map<Integer, Integer> rankMap;
public int reversePairs(int[] nums) {
int result = 0;
if( nums==null || nums.length==0 ) {
return result;
}
buildRankMap(nums);
FenwickTree fenwickTree = new FenwickTree( nums.length+1 );
for(int i=0; i<nums.length; i++) {
int rankNum = rankMap.get(nums[i]);
int allNum = i;
int pairNum = fenwickTree.getPrefixSum( rankNum );
int reversePairNum = allNum - pairNum;
fenwickTree.update(rankNum,1);
result += reversePairNum;
}
return result;
}
private void buildRankMap(int[] nums) {
int[] temp = Arrays.stream(nums)
.distinct()
.sorted()
.toArray();
rankMap = new HashMap<>();
for(int i=0; i<temp.length; i++) {
rankMap.put(temp[i], i+1);
}
}
public static class FenwickTree {
private int[] bit;
public FenwickTree(int size) {
bit = new int[size];
}
public int getPrefixSum(int index) {
int sum = 0;
while (index>0) {
sum += bit[index];
index = index - lowbit(index);
}
return sum;
}
public void update(int index, int delta) {
while (index<bit.length) {
bit[index] += delta;
index = index + lowbit(index);
}
}
private int lowbit(int num) {
return num & -num ;
}
}
}
|








