浅谈二叉树遍历

这里就对二叉树的遍历方式进行总结

基于递归的遍历

前序遍历

前序遍历：即对二叉树按照当前节点、左子树、右子树的顺序进行遍历。显然借助递归，非常容易实现、理解

/**
 * 基于递归的前序遍历
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new LinkedList<>();
        dfs(root, list);
        return list;
    }

    private void dfs(TreeNode cur, List<Integer> list) {
        if( cur==null ) {
            return;
        }

        // 1. 处理当前节点
        list.add( cur.val );

        // 2. 处理左子树
        dfs(cur.left, list);

        // 3. 处理右子树
        dfs(cur.right, list);
    }
}

中序遍历

中序遍历：即对二叉树按照左子树、当前节点、右子树的顺序进行遍历。显然借助递归，非常容易实现、理解

/**
 * 基于递归的中序遍历
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new LinkedList<>();
        dfs(root, list);
        return list;
    }

    private void dfs(TreeNode cur, List<Integer> list) {
        if( cur==null ) {
            return;
        }

        // 1. 处理左子树
        dfs(cur.left, list);

        // 2. 处理当前节点
        list.add( cur.val );

        // 3. 处理右子树
        dfs(cur.right, list);
    }
}

后序遍历

后序遍历：即对二叉树按照左子树、右子树、当前节点的顺序进行遍历。显然借助递归，非常容易实现、理解

/**
 * 基于递归的后序遍历
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new LinkedList<>();
        dfs(root, list);
        return list;
    }

    private void dfs(TreeNode cur, List<Integer> list) {
        if( cur==null ) {
            return;
        }

        // 1. 处理左子树
        dfs(cur.left, list);

        // 2. 处理右子树
        dfs(cur.right, list);

        // 3. 处理当前节点
        list.add( cur.val );
    }
}

基于迭代的遍历

前序遍历

不同于递归隐式维护栈的便捷，在通过迭代进行遍历时需要我们显式地维护一个栈。具体地，在前序遍历当中。首先需要处理对当前节点进行处理、然后沿着左子树一直入栈。当左子树遍历完毕, 通过出栈获取父节点来对右子树再进行处理

/**
 * 基于迭代的前序遍历
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        LinkedList<TreeNode> stack = new LinkedList<>();

        while ( root!=null || !stack.isEmpty() ) {
            while (root!=null) {
                // 先处理当前节点
                res.add( root.val );
                // 然后沿左子树一直入栈
                stack.addLast( root );
                root = root.left;
            }

            // 左子树遍历完毕, 通过父节点来对右子树再进行处理
            TreeNode parent = stack.removeLast();
            root = parent.right;
        }

        return res;
    }
}

中序遍历

不同于递归隐式维护栈的便捷，在通过迭代进行遍历时需要我们显式地维护一个栈。具体地，在中序遍历当中。首先沿着左子树一直入栈。当左子树遍历完毕, 通过出栈获取父节点并对其进行处理，最后对右子树再进行处理

/**
 * 基于迭代的中序遍历
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        LinkedList<TreeNode> stack = new LinkedList<>();

        while ( root!=null || !stack.isEmpty() ) {
            while ( root!=null ) {
                // 先沿左子树一直入栈
                stack.addLast( root );
                root = root.left;
            }

            // 左子树遍历完毕, 获取父节点
            TreeNode parent = stack.removeLast();
            // 处理父节点的值
            res.add( parent.val );
            // 通过父节点对右子树再进行处理
            root = parent.right;
        }

        return res;
    }
}

后序遍历

后序遍历的顺序是左、右、当前。如果直接使用栈按这个顺序进行遍历输出会比较麻烦。故我们可以先按照当前、右、左的顺序进行迭代遍历，显然这个过程与前序遍历非常类似，只是需要把代码中涉及左、右子树的调换下即可。最后对遍历结果进行翻转。这样遍历结果就由当前、右、左 就变为 左、右、当前。即我们所需的后序遍历结果

/**
 * 基于迭代的后序遍历
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        LinkedList<TreeNode> stack = new LinkedList<>();

        // 先按 根、右、左 的顺序进行遍历
        while ( root!=null || !stack.isEmpty() ) {
            while (root!=null) {
                // 先处理当前节点
                res.add( root.val );
                // 然后沿右子树一直入栈
                stack.addLast( root );
                root = root.right;
            }

            // 右子树遍历完毕, 通过父节点获取左子树再进行处理
            TreeNode parent = stack.removeLast();
            root = parent.left;
        }

        // 对遍历结果进行翻转
        // 这样遍历结果就由 根、右、左 就变为 左、右、根, 即后序遍历
        Collections.reverse( res );
        return res;
    }
}

层序遍历

对于二叉树的层序遍历就简单很多了。我们借助队列的FIFO特性即可轻松实现

class Solution {
    public List<Integer> levelOrder(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        if (root == null) {
            return res;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);

        while ( !queue.isEmpty() ) {
            // 弹出队首元素, 进行处理
            TreeNode cur = queue.poll();
            res.add( node.val );

            // 将当前节点的左、右子节点加入队列
            if( node.left != null ) {
                queue.add( node.left );    
            }           
            if( node.right != null ) {
                queue.add( node.right );    
            }
        }

        return res;
    }
}

基于Morris算法的遍历

基本原理

Morris算法为二叉树的遍历提供了新的思路，其通过充分利用树中叶子节点存在大量空指针这一特点。实现了常数级别的空间复杂度。在进一步介绍该算法之前，我们先来说明一个概念——mostRight节点。其用于表示当前节点cur的左子树的最右节点。例如下图的一个二叉树。如果当前节点为1，则mostRight节点即为5；如果当前节点为3，则mostRight节点即为6

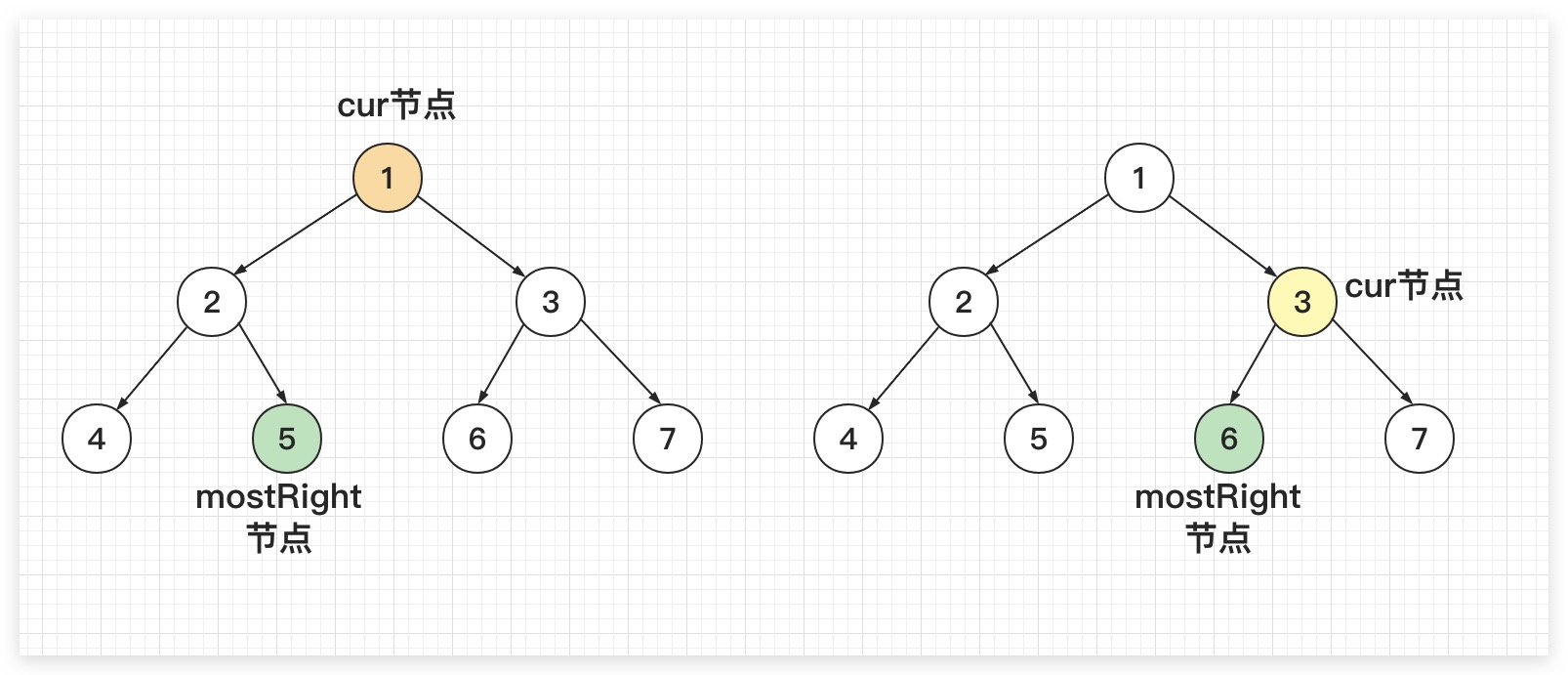
实际上，Morris算法非常简单。其基本遍历流程如下：

1. 将当前节点cur初始化为root
2. 当前节点cur如果不存在左子树。则将当前节点指向其右子树，以便遍历当前节点的右子树
3. 当前节点cur如果存在左子树，则先获取cur节点的mostRight节点
   • 如果mostRight节点的右子节点为空，此时说明cur节点的左子树还未遍历。故：一方面，我们将mostRight节点的右子节点设置为cur节点；另一方面，将当前节点指向其左子树，以便遍历当前节点的左子树
   • 如果mostRight节点的右子节点为当前节点cur，此时说明cur节点的左子树已经遍历完成。故：一方面，我们将mostRight节点的右子节点设置为null空指针；另一方面，将当前节点指向其右子树，以便遍历当前节点的右子树
4. 重复Step 2、Step 3，直到当前节点cur为null时为止

该算法遍历过程的示意图如下，可以看到当一个节点的左子树未遍历完时，Morris算法会利用原叶子节点的null空指针修改树。而当该节点的左子树遍历后，会把对树的修改进行撤回。以恢复树原有的结构

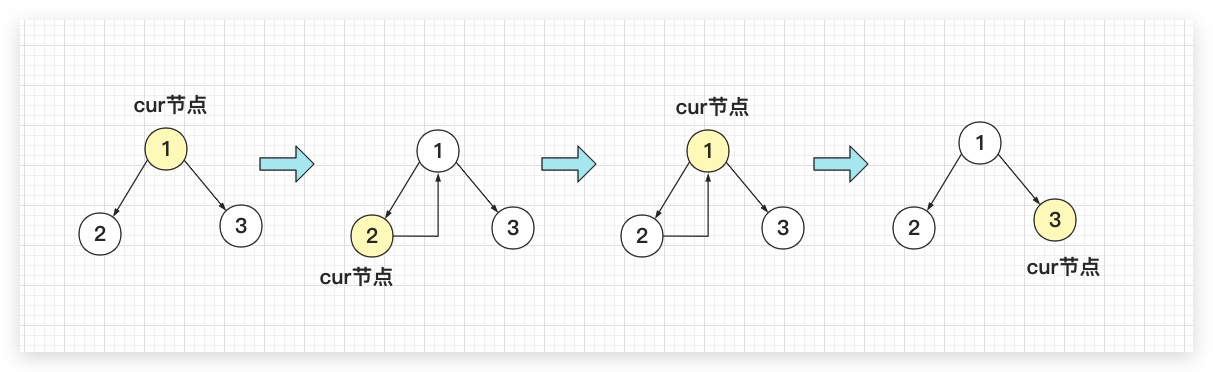
前序遍历

这里基于Morris算法来实现前序遍历。问题的关键就在于何时对当前节点进行处理。显然这里有两个时机，一方面，遍历过程中发现当前节点的左子树为空。则在对当前节点的右子树进行遍历前，需要对当前节点进行处理；另一方面，遍历过程中发现当前节点的左子树不为空，则在对当前节点的左子树进行遍历前，需要对当前节点进行处理

/**
 * 基于Morris算法的前序遍历
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        if( root == null ) {
            return res;
        }

        TreeNode cur = root;
        // 当前节点cur的左子树的最右节点
        TreeNode mostRight = null;

        while ( cur != null ) {
            // 当前节点的左子树为空
            if( cur.left == null ) {
                // 处理当前节点
                res.add( cur.val );
                // 处理当前节点的右子树
                cur = cur.right;
            } else {    // 当前节点的左子树不为空
                // 寻找当前节点cur的左子树的最右节点
                mostRight = cur.left;
                while ( mostRight.right!=null && mostRight.right!=cur ) {
                    mostRight = mostRight.right;
                }

                if( mostRight.right == null) {  // 说明cur节点的左子树未遍历
                    // 处理当前节点
                    res.add( cur.val );
                    // 处理当前节点的左子树
                    mostRight.right = cur;
                    cur = cur.left;
                } else if ( mostRight.right == cur ) {  // 说明cur节点的左子树已经遍历完成
                    // 处理当前节点的右子树
                    mostRight.right = null;
                    cur = cur.right;
                }
            }
        }

        return res;
    }
}

中序遍历

这里基于Morris算法来实现中序遍历。问题的关键就在于何时对当前节点进行处理。显然这里有两个时机，一方面，遍历过程中发现当前节点的左子树为空。则在对当前节点的右子树进行遍历前，需要对当前节点进行处理；另一方面，遍历过程中发现当前节点的左子树不为空，则在对当前节点的左子树完成遍历后，需要对当前节点进行处理

/**
 * 基于Morris算法的中序遍历
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new LinkedList<>();
        if( root == null ) {
            return res;
        }

        TreeNode cur = root;
        // 当前节点cur的左子树的最右节点
        TreeNode mostRight = null;

        while ( cur != null ) {
            // 当前节点的左子树为空
            if( cur.left == null ) {
                // 处理当前节点
                res.add( cur.val );
                // 处理当前节点的右子树
                cur = cur.right;
            } else {    // 当前节点的左子树不为空
                // 寻找当前节点cur的左子树的最右节点
                mostRight = cur.left;
                while ( mostRight.right!=null && mostRight.right!=cur ) {
                    mostRight = mostRight.right;
                }

                if( mostRight.right == null) {  // 说明cur节点的左子树未遍历
                    // 处理当前节点的左子树
                    mostRight.right = cur;
                    cur = cur.left;
                } else if ( mostRight.right == cur ) {  // 说明cur节点的左子树已经遍历完成
                    // 处理当前节点
                    res.add( cur.val );
                    // 处理当前节点的右子树
                    mostRight.right = null;
                    cur = cur.right;
                }
            }
        }

        return res;
    }
}

Note

这里给出本文中关于树节点的类定义

/**
 * 树的节点
 */
class TreeNode {
    TreeNode left;
    
    TreeNode right;
    
    int val;
    
    TreeNode() {
    }
    
    TreeNode(int val) {
        this.val = val; 
    }
    
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}