在组合数学中，Stirling Number 斯特林数具体可分为两种：第一类斯特林数、第二类斯特林数。由18世纪数学家James Stirling提出、命名

第一类斯特林数

第一类斯特林数s(n,k)表示将n个不同元素构成k个圆排列的方法数。也可使用下述记法

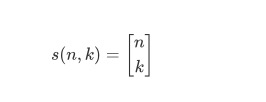
显然,
当k=0时，如果n>0，有s(n,k)=0
当k=n时，s(n,k)=1

特别地，规定当k=0、n=0时，s(n,k)=1

现在通过举例的方式进行计算

从3个不同的元素构成1个圆排列的方法有：
[A,B,C] , [A,C,B]
故，s(3,1)=2

从3个不同的元素构成2个圆排列的方法有：
[A,B][C] , [A,C][B] , [B,C][A]
故，s(3,2)=3

现在如果我们期望计算s(4,2)，则有两个思路：
要么将前3个元素构成一个圆排列，第4个元素单独构成一个圆排列。即：[A,B,C][D] , [A,C,B][D]
要么将第4个元素放进由前3个元素所构成的2个圆排列当中。即：
[A,D,B][C] , [A,B,D][C] , [A,B][C,D] ,
[A,D,C][B] , [A,C,D][B] , [A,C][B,D] ,
[B,D,C][A] , [B,C,D][A] , [B,C][A,D]
故，根据加法原理易知：s(4,2)=2+9=11

事实上，通过计算s(4,2)的过程中，我们已经发现了计算s(n,k)的一般方法。即：要么将最后一个元素单独构成一个圆排列；要么将最后一个元素放进由前n-1个元素所构成的k个圆排列当中（显然对于由n-1个元素所构成的若干个圆排列而言，第n个元素可插入的位置有n-1个）。故：

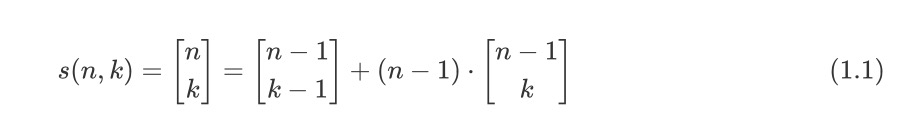
第一类斯特林数的斯特林三角如下所示

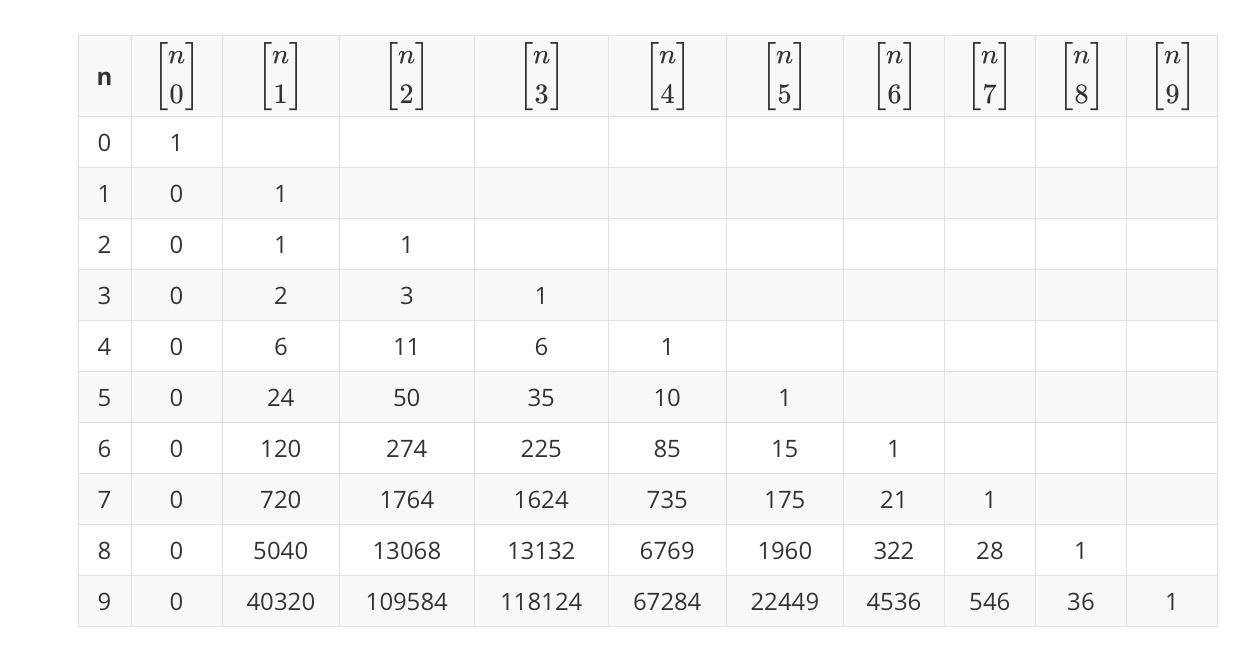
事实上，第一类斯特林数还可以作为将升阶乘、降阶乘转换为普通幂的系数

例如，对于升阶乘：

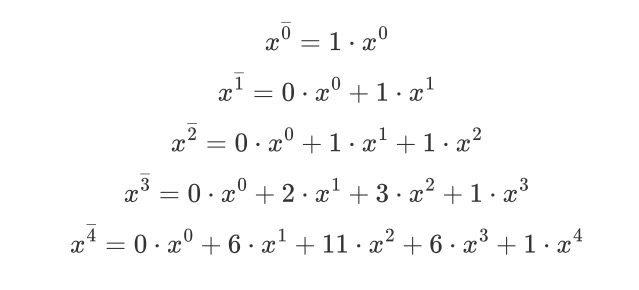
例如，对于降阶乘：

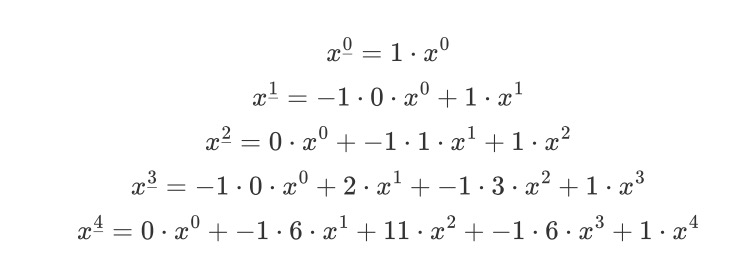
第二类斯特林数

第二类斯特林数S(n,k)表示将n个不同元素构成k个非空子集的方法数。也可使用下述记法

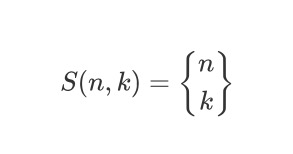
显然,
当k=0时，如果n>0，有S(n,k)=0
当k=n时，S(n,k)=1

特别地，规定当k=0、n=0时，S(n,k)=1

现在通过举例的方式进行计算

从3个不同的元素构成1个非空子集的方法有：
{A,B,C}
故，S(3,1)=1

从3个不同的元素构成2个非空子集的方法有：
{A,B}{C} , {A,C}{B} , {B,C}{A}
故，S(3,2)=3

现在如果我们期望计算S(4,2)，则有两个思路：
要么将前3个元素构成一个非空子集，第4个元素单独构成一个非空子集。即：{A,B,C}{D}
要么将第4个元素放进由前3个元素所构成的2个非空子集当中。即：
{A,B,D}{C} , {A,C,D}{B} , {B,C,D}{A} ,
{A,B}{C,D} , {A,C}{B,D} , {B,C}{A,D}
故，根据加法原理易知：S(4,2)=1+6=7

事实上，通过计算S(4,2)的过程中，我们已经发现了计算S(n,k)的一般方法。即：要么将最后一个元素单独构成一个非空子集；要么将最后一个元素放进由前n-1个元素所构成的k个非空子集当中（显然对于由n-1个元素所构成的k个非空子集而言，第n个元素可插入的位置有k个）。故：

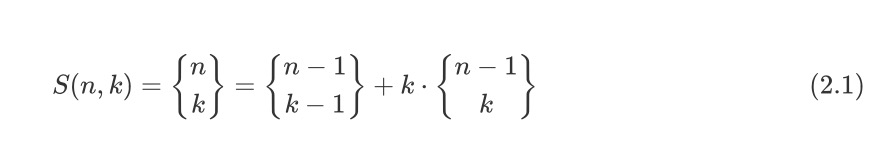
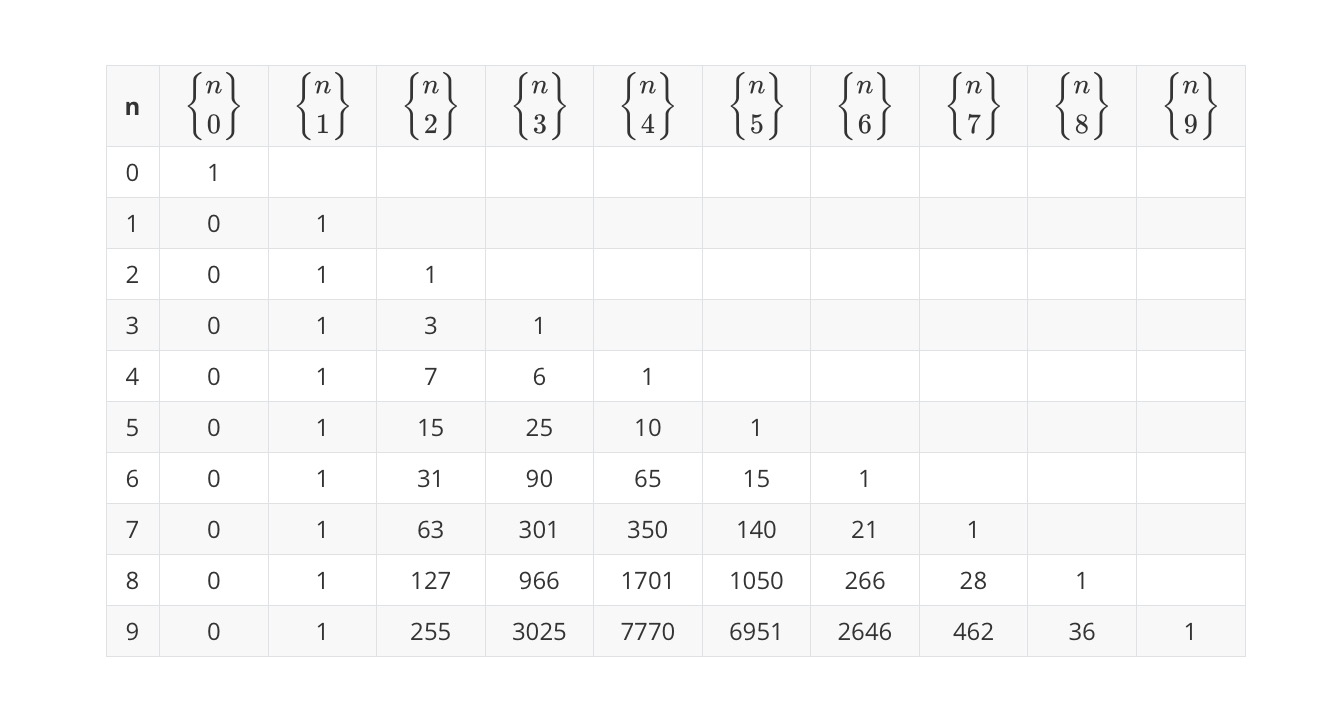
第二类斯特林数的斯特林三角如下所示

事实上，第二类斯特林数还可以作为将普通幂转换为降阶乘、升阶乘的系数

例如，将普通幂转换为降阶乘：

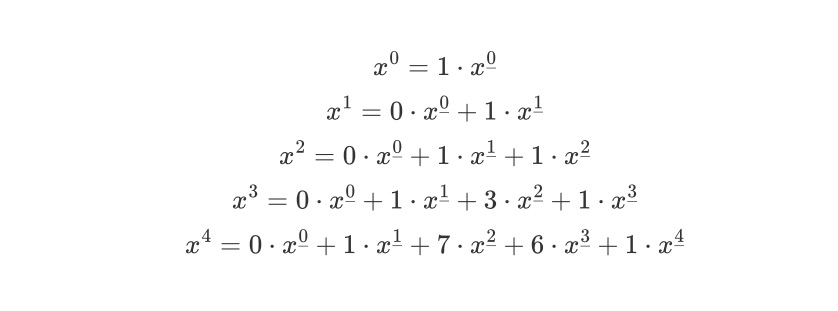
例如，将普通幂转换为升阶乘：

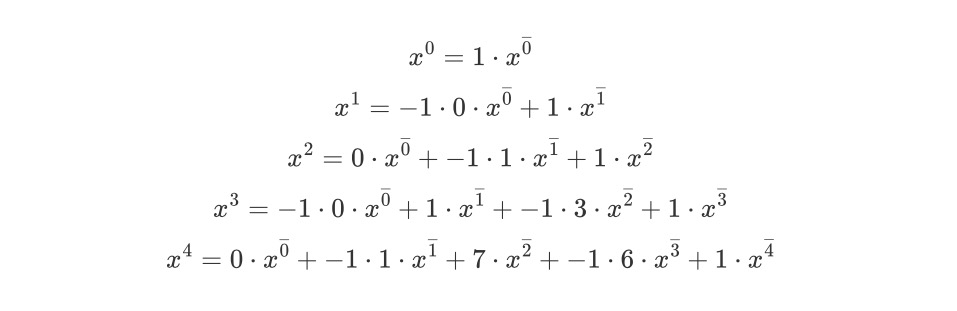
实践

学习过程中要善于理论联系实际。故在介绍完经验总结后，这里以LeetCode的第1866题——恰有 K 根木棍可以看到的排列数目为例进行实践

有n根长度互不相同的木棍，长度为从1到n的整数。请你将这些木棍排成一排，并满足从左侧可以看到恰好k根木棍。从左侧可以看到木棍的前提是这个木棍的左侧不存在比它更长的木棍。
其中：1 <= n <= 1000；1 <= k <= n
例如，如果木棍排列为 [1,3,2,5,4] ，那么从左侧可以看到的就是长度分别为 1、3 、5 的木棍。
给你 n 和 k ，返回符合题目要求的排列数目。由于答案可能很大，请返回对 10^9 + 7 取余的结果。

示例 1
输入：n = 3, k = 2
输出：3
解释：[1,3,2], [2,3,1] 和 [2,1,3] 是仅有的能满足恰好 2 根木棍可以看到的排列。
可以看到的木棍已经用粗体标识。

示例 2
输入：n = 5, k = 5
输出：1
解释：[1,2,3,4,5] 是唯一一种能满足全部 5 根木棍可以看到的排列。
可以看到的木棍已经用粗体标识。

示例 3
输入：n = 20, k = 11
输出：647427950
解释：总共有 647427950 (mod 10^9+7) 种能满足恰好有 11 根木棍可以看到的排列。

题解思路：首先我们将每根能看到的木棍及其后面被挡住的木棍看作一个整体，此时n根木棍就被划分成了k个部分，显然每个部分的第一根木棍即为可以看到的木棍。为此对于任意一个含m根木棍的部分而言，我们必须把该部分中最长的木棍固定在该部分的第一个位置，而剩余的m-1根木棍则可以任意排列。故此时对于一个含m根木棍的部分，其允许的排列方法数为 (m-1)! 。显然不难看出，本质上这其实就是，对一个含m根木棍的部分进行圆排列的方法数。到这里，原问题就被转换为计算n根木棍构成k个非空圆排列的方法数。即所谓的第一类斯特林数。代码示例如下

/**
 * 组合数学：第一类斯特林数
 */
class Solution {
    private static long mod = 1_000_000_007;

    public int rearrangeSticks(int n, int k) {
        if( n==k ) {
            return 1;
        } else if( n<k ) {
            return 0;
        } else if( n>0 && k==0 ) {
            return 0;
        }

        long[][] dp = new long[2][k+1];
        dp[0][0] = 1;
        int newIndex = 0;
        for (int i=1; i<=n; i++) {
            newIndex = 1 - newIndex;
            int oldIndex = 1 - newIndex;

            dp[newIndex][0] = 0;    // s(n,0) = 0
            // 当k>n时有s(n,k)=0, 故增加j<=i条件进行剪枝
            for (int j=1; j<=k && j<=i ; j++) {
                dp[newIndex][j] = ( dp[oldIndex][j-1] + (i-1)*dp[oldIndex][j] ) % mod;
            }
        }

        return (int)dp[newIndex][k];
    }
}

参考文献

具体数学·第2版 Ronald L.Graham、Oren Patashnik、Donald E.Knuth著

xyZGHio

浅谈Stirling Number斯特林数

第一类斯特林数

第二类斯特林数

实践

参考文献