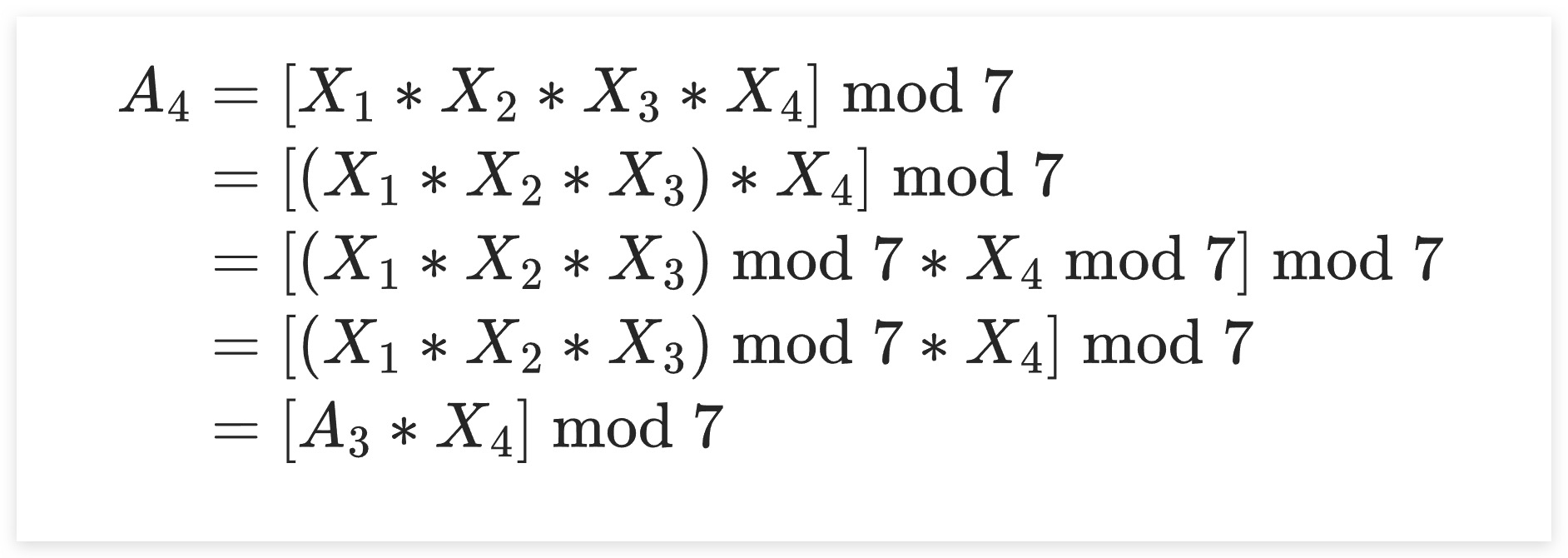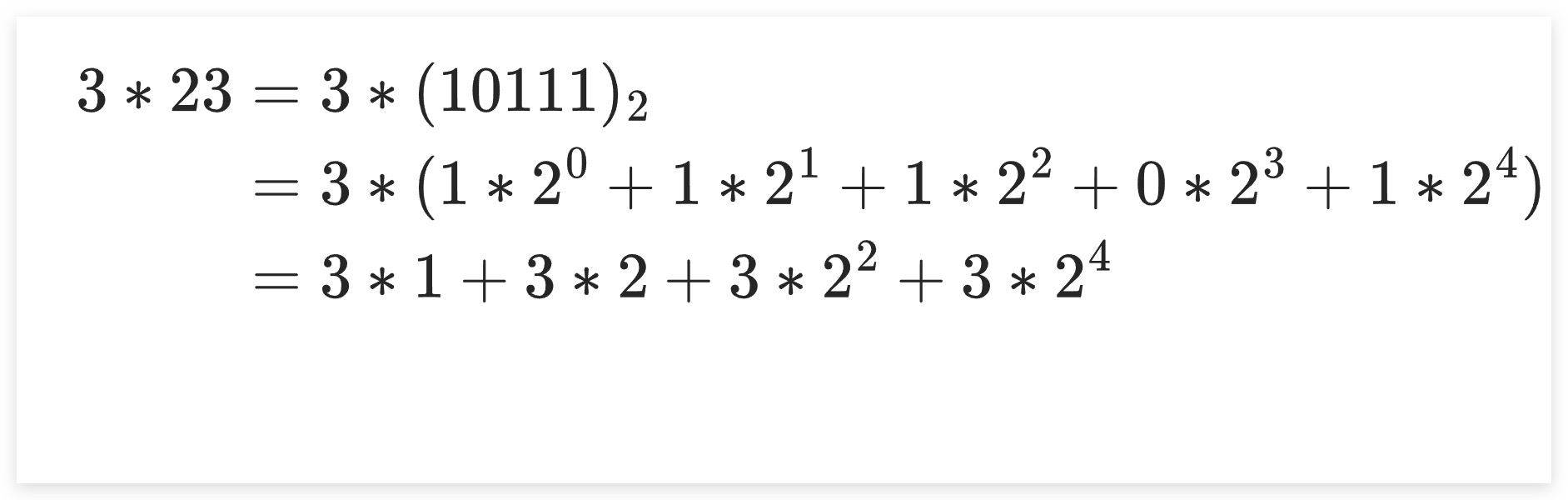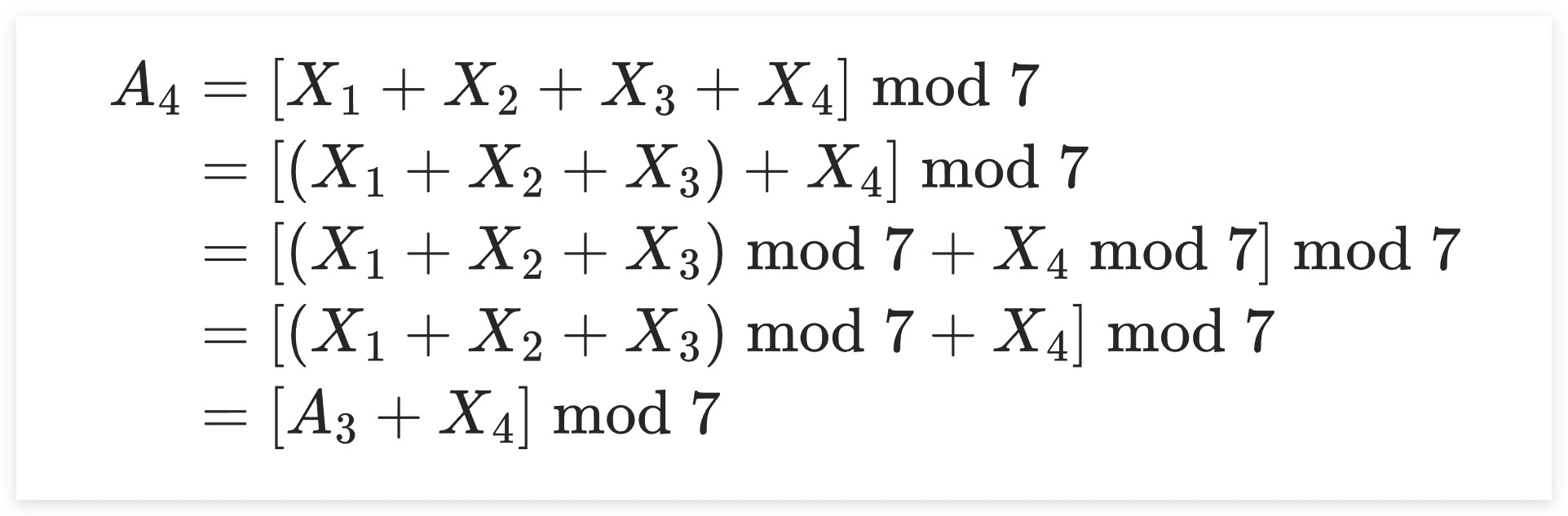本文简要介绍快速幂、快速乘等算法，并与取模运算进行结合

快速幂

所谓快速幂，指的是快速计算幂的方法。例如计算3的23次幂，如果采用朴素的方式一次一次地乘3，需要进行22次。其时间复杂度为线性时间。而如果转换思路，我们将指数的23改为采用二进制表示：10111。如下所示，可以看到，变成若干个乘数（即下图的3的1次方、3的2次方、3的4次方、3的16次方）进行相乘。其中每个乘数是前一个乘数的平方。特别地，对于指数相应二进制位为0的乘数（例如下图红框中3的8次方），则在最终计算过程中直接跳过即可。可以看到，快速幂的时间复杂度为对数时间

Java版本实现如下所示

/**
 * 快速幂
 * @param base 底数
 * @param exp 指数
 * @return
 */
public static long quickPower(long base, long exp) {
    // 乘法单位元为1
    long result = 1;
    long temp = base;
    while (exp!=0) {
        // 取出指数在二进制下的最后一位
        long lastBit = exp&1;
        // 该位不为0, 说明最终计算结果需要乘上这个中间乘数
        if( lastBit!=0 ) {
            result *= temp;
        }
        // 更新中间乘数
        temp *= temp;
        // 移除指数在二进制下的最后一位
        exp >>= 1;
    }
    return result;
}

模幂运算

在快速幂的基础上，我们来看下如何进行模幂运算。即形如“(x^y) mod z”。在进一步展开前，我们先介绍下模在乘法下的运算规则

1 2	// 乘积的模等于各乘数分别取模后求积、并对积再取一次模 (a·b) mod z = [(a mod z)·(b mod z)] mod z

这里，我们以（3^23）mod 7 为例进行说明。结合快速幂、模运算规则进行转换如下所示，可以看到转换后的各乘数X实际上是对前一个X的平方再取模的结果，体现在下述代码的(2)处

这里我们令X1～X4乘积后进行取模的结果为A4，再次运用模运算规则进行转换。由于X4肯定小于7，故X4 mod 7 可以直接化简为X4。同时令X1～X3乘积后进行取模的结果为A3。可以看到其揭示了我们在后面进行迭代计算过程中的递推公式，体现在下述代码的(1)处

此时，我们就可以利用快速幂实现模幂运算，Java实现如下所示

/**
 * 模幂运算
 * @param base 底数
 * @param exp 指数
 * @param n 模
 * @return
 */
public static long modPower(long base, long exp, long n) {
    // 乘法单位元为1
    long result = 1;
    // 即公式中的X1
    long temp = base % n;
    while (exp!=0) {
        // 取出指数在二进制下的最后一位
        long lastBit = exp&1;
        // 该位不为0, 说明最终计算结果需要乘上这个中间乘数
        if( lastBit!=0 ) {
            // 此处应用迭代计算过程的递推公式
            result = (result * temp) % n;  // (1)
        }
        // 更新中间乘数: 对前一个乘数进行平方再取模
        temp = (temp * temp) % n;   // (2)
        // 移除指数在二进制下的最后一位
        exp >>= 1;
    }
    return result;
}

快速乘

介绍完快速幂，相应的快速乘就简单很多了。其基本原理也是类似的，将其中的一个乘数按二进制进行拆分，然后利用分配律将乘法转换为加法。可以看到，一方面，对于两个大数相乘的场景，快速乘通过将乘法变为加法大大提高其在计算机中的运算效率；另一方面，对于大数的模乘运算而言，形如“(x·y) mod z”。借助快速乘可以防止两个大数的乘积直接溢出。典型地，模乘运算广泛存在于RSA计算当中

例如计算3x23，我们将其中一个乘数23改为采用二进制表示：10111，然后采用乘法的分配律将其改写加法。类似地，可以看到各加数均是前一个加数的两倍

Java实现如下所示

/**
 * 快速乘
 * @param num1 乘数1
 * @param num2 乘数2
 * @return
 */
public static long quickMultiply(long num1, long num2) {
    // 加法单位元为0
    long result = 0;
    long temp = num1;
    while (num2!=0) {
        // 取出num2在二进制下的最后一位
        long lastBit = num2&1;
        // 该位不为0, 说明最终计算结果需要加上这个中间数
        if( lastBit!=0 ) {
            result += temp;
        }
        // 更新中间数
        temp += temp;
        // 移除指数在二进制下的最后一位
        num2 >>= 1;
    }
    return result;
}

模乘运算

在快速乘的基础上，我们来看下如何进行模乘运算。即形如“(x·y) mod z”。在进一步展开前，我们先介绍下模在加法下的运算规则

1 2	// 和的模等于各数分别取模后求和、并对和再取一次模 (a+b) mod z = [(a mod z)+(b mod z)] mod z

这里，我们以（3x23）mod 7 为例进行说明。结合快速乘、模运算规则进行转换如下所示，可以看到转换后的各加数X实际上是前一个X的两倍再取模的结果，体现在下述代码的(2)处

这里我们令X1～X4之和进行取模的结果为A4，再次运用模运算规则进行转换。由于X4肯定小于7，故X4 mod 7 可以直接化简为X4。同时令X1～X3之和进行取模的结果为A3。可以看到其揭示了我们在后面进行迭代计算过程中的递推公式，体现在下述代码的(1)处

此时，我们就可以利用快速乘实现模乘运算，Java实现如下所示

/**
 * 模乘运算
 * @param num1 乘数1
 * @param num2 乘数2
 * @param n 模
 * @return
 */
public static long modMultiply(long num1, long num2, long n) {
    // 加法单位元为0
    long result = 0;
    // 即公式中的X1
    long temp = num1 % n;
    while (num2!=0) {
        // 取出num2在二进制下的最后一位
        long lastBit = num2&1;
        // 该位不为0, 说明最终计算结果需要加上这个中间数
        if( lastBit!=0 ) {
            // 此处应用迭代计算过程递推公式
            result = (result + temp) % n;   //（1）
        }
        // 更新中间数: 对前一个数翻倍再取模
        temp = (temp+temp) % n; // (2)
        // 移除指数在二进制下的最后一位
        num2 >>= 1;
    }
    return result;
}

矩阵快速幂

前面我们提到了快速幂，故这里就矩阵的快速幂作一下补充说明。首先，对于矩阵形式的快速幂而言，其与普通的快速幂在基本原理上没有差别，都是将指数部分转换为二进制进行处理。但需要注意的是对于矩阵乘法而言，其乘法的单位元是单位矩阵。这里给出基于Groovy的矩阵快速幂实现。借助于Groovy的运算符重载特性，可以很方便的进行矩阵乘法运算

class Matrix {
    /**
     * 矩阵阶数
     */
    int n

    /**
     * 矩阵数据
     */
    List<List<Long>> mat

    Matrix(List<List<Long>> initValue) {
        this.n = initValue.size()
        // 初始化矩阵数据
        this.mat = initValue
    }

    /**
     * 重载 * 乘法运算符, 实现矩阵乘法
     * @param other
     * @return
     */
    Matrix multiply(Matrix other) {
        List<List<Long>> resultData = []
        for( row in 0..<n ) {
            List<Long> rowList = []
            for( col in 0..<n ) {
                def num = 0l
                (0..<n).each { i ->
                    num += this.mat[row][i] * other.mat[i][col]
                }
                rowList << num
            }
            resultData << rowList
        }
        return new Matrix(resultData)
    }

    /**
     * 获取n阶单位矩阵
     * @param n 阶数
     * @return
     */
    static Matrix identityMat(int n) {
        List<List<Long>> resultData = new ArrayList<>(n)
        (0..<n).each { i ->
            List<Long> subList = new ArrayList<>( Collections.nCopies(n,0l) )
            subList[i] = 1l
            resultData << subList
        }
        return new Matrix(resultData)
    }

    /**
     * 矩阵快速幂
     * @param matrix n阶方阵
     * @param exp 指数
     * @return
     */
    static Matrix quickMatrixPower(Matrix matrix, long exp) {
        // 矩阵乘法单位元: n阶单位矩阵
        Matrix result = Matrix.identityMat( matrix.n )
        Matrix temp = matrix
        while (exp!=0) {
            // 取出指数在二进制下的最后一位
            long lastBit = exp&1
            // 该位不为0, 说明最终计算结果需要乘上这个中间乘数
            if( lastBit!=0 ) {
                result = result * temp
            }
            // 更新中间乘数
            temp = temp * temp
            // 移除指数在二进制下的最后一位
            exp >>= 1
        }
        return result
    }
}

xyZGHio

浅谈乘法

快速幂

模幂运算

快速乘

模乘运算

矩阵快速幂