这里介绍普通二分查找问题、存在重复元素的二分查找问题的解题思路

普通的二分查找问题

左闭右闭区间

左闭右闭区间的二分查找算法模板如下所示。其要点在于：

right变量初值为数组最后一个元素下标，故搜索区间是一个左闭右闭区间 [left, right]
由于搜索区间为左闭右闭区间。因此当left等于right时，依然存在待搜索元素。故还需要继续查找，所以while条件是 left <= right
每轮遍历过程中，mid位置的元素将其划分为三个区间：[left, mid-1]、mid、[mid+1, right]。故当判断在左侧区间时，需要更新right值为mid-1；当判断在右侧区间时，需要更新left值为mid+1

/**
 * 二分查找, 判断指定元素是否存在于数组
 * @param array
 * @param target
 * @return
 */
public boolean binarySearch(int[] array, int target) {
    // 左闭右闭区间: [left, right]
    int left = 0;
    int right = array.length-1;

    // 由于为左闭右闭区间, 故在left等于right的场景下, 也需要继续查找
    while (left <= right) {
        // 防止left+right直接相加发生溢出
        int mid = left + (right-left)/2;
        if( target == array[mid] ) {
            // 找到目标元素, 返回true
            return true;
        } else if( target < array[mid] ) {
            // 目标元素在左侧区间, 即 [left, mid-1]
            // 故更新right值
            right = mid - 1;
        } else if( target > array[mid] ) {
            // 目标元素在右侧区间, 即 [mid+1, right]
            // 故更新left值
            left = mid + 1;
        }
    }
    return false;
}

左闭右开区间

左闭右开区间的二分查找算法模板如下所示。其要点在于：

right变量初值为数组长度，故搜索区间是一个左闭右开区间 [left, right)
由于搜索区间为左闭右开区间，因此当left等于right时，不存在待搜索元素，故不需要继续查找。比如在[3,3)区间中显然不可能存在一个整数。所以while条件是 left < right
每轮遍历过程中，mid位置的元素将其划分为三个区间：[left, mid)、[mid]、[mid+1, right)。故当判断分别在左、右侧区间时，需更新相应的left、right值。需要注意的是如果目标元素在左侧区间[left, mid)，由于本轮迭代mid位置的元素已经判断过了，mid位置可以直接作为下一轮迭代的右开端点；但如果目标元素在右侧区间[mid+1, right)，则下一轮迭代过程需要以mid+1作为左闭端点

/**
 * 二分查找, 判断指定元素是否存在于数组
 * @param array
 * @param target
 * @return
 */
public boolean binarySearch(int[] array, int target) {
    // 左闭右闭区间: [left, right)
    int left = 0;
    int right = array.length;

    // 由于为左闭右开区间, 故在left等于right的场景下, 不需要继续查找
    // 比如在[3,3)区间中显然不可能存在一个整数
    while (left < right) {
        // 防止left+right直接相加发生溢出
        int mid = left + (right-left)/2;
        if( target == array[mid] ) {
            // 找到目标元素, 返回true
            return true;
        } else if( target < array[mid] ) {
            // 目标元素在左侧区间, 即 [left, mid)
            // 故更新right值
            right = mid;
        } else if( target > array[mid] ) {
            // 目标元素在右侧区间, 即 [mid+1, right)
            // 故更新left值
            left = mid + 1;
        }
    }
    return false;
}

总结

对于普通二分查找的场景，强烈推荐使用第一种模板思路，即左闭右闭区间的思路。因为其判断条件简单、区间边界值更新具有对称性，便于思考、记忆，减少心智负担

存在重复元素的二分查找问题

查找元素第一次出现的位置

对于一个存在重复元素的有序数组而言。如果元素存在于该数组中，则期望找出元素在该数组中第一次出现的下标位置；否则均返回-1，表示元素不存在于该数组

基于上述对两种二分查找模板的结论，我们选择采用左闭右闭区间的思路来进行二分查找。首先，我们思考基本的二分查找，不难得出下述结论：

结论1：right指针右侧的元素（不包含right指针指向的元素）一定是大于目标值
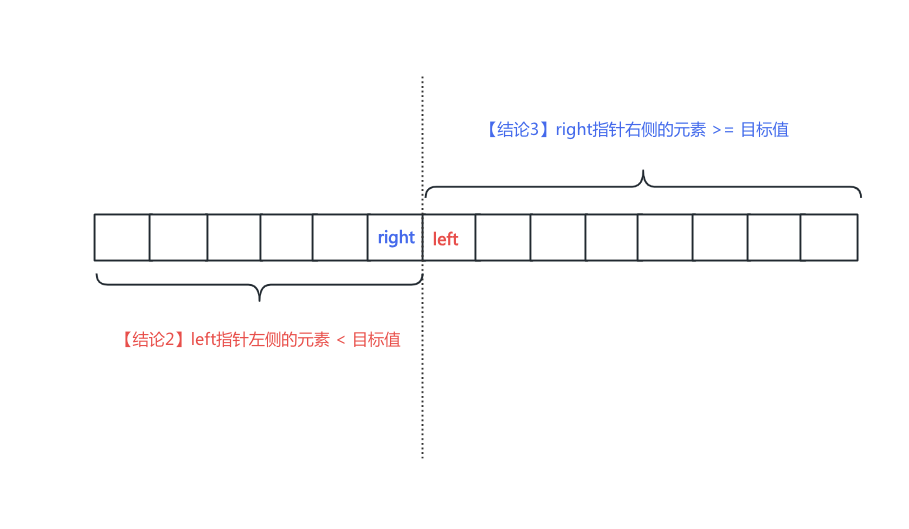
结论2：left指针左侧的元素（不包含left指针指向的元素）一定是小于目标值

这里，由于需要寻找元素第一次出现的位置。故当nums[mid]与目标值相等时，我们依然需要继续搜索左区间（显然是更新right指针为mid-1）。因为此时mid所指向的位置并不一定是该元素第一次的位置，关于这一点也很好理解

但此时需要注意，当nums[mid]与目标值相等时，我们会继续搜索左区间。这样其实会导致原有结论1发生变化，即：

结论3：right指针右侧的元素（不包含right指针指向的元素）一定是 大于等于 目标值

由于循环条件为 left <= right。故当整个二分查找的循环结束后，必定有right+1=left。利用结论2、结论3，结合下图。我们知道如果这个有序数组中存在目标值的元素。那么它第一次出现的位置一定是right指针右侧的第一个元素，由于right+1=left，即为left指针指向的元素。但需要注意的是该数组中也可能不存在目标值的元素，故最后还应该对left指针指向的元素进行检验：边界检查、值检查

/**
 * 寻找元素重复出现时的第一个位置(即，左下标)
 * @param nums 存在重复元素的有序数组
 * @param target 目标元素值
 * @return
 */
private int findLeftIndex(int[] nums, int target) {
    int left = 0;
    int right = nums.length-1;
    while (left<=right) {
        int mid = left + (right-left)/2;
        if ( target<nums[mid] ) {
            // 目标元素在左侧区间, 即 [left, mid-1]
            // 故更新right值
            right = mid-1;
        } else if ( target>nums[mid] ) {
            // 目标元素在右侧区间, 即 [mid+1, right]
            // 故更新left值
            left = mid+1;
        } else if( target==nums[mid] ) {
            // 在找到目标值后继续寻找左边界, 需要继续搜索左区间
            // 故更新right值
            right = mid-1;
        }
    }

    // 边界检查、值检查: 防止查找元素不存在
    if ( left>=0 && left<nums.length && nums[left] == target ) {
        return left;
    } else {
        // 元素不存在
        return -1;
    }
}

查找元素最后一次出现的位置

对于一个存在重复元素的有序数组而言。如果元素存在于该数组中，则期望找出元素在该数组中最后一次出现的下标位置；否则均返回-1，表示元素不存在于该数组

类似地，基于上述对两种二分查找模板的结论。我们选择采用左闭右闭区间的思路来进行二分查找。首先，我们思考基本的二分查找，同样不难得出下述结论：

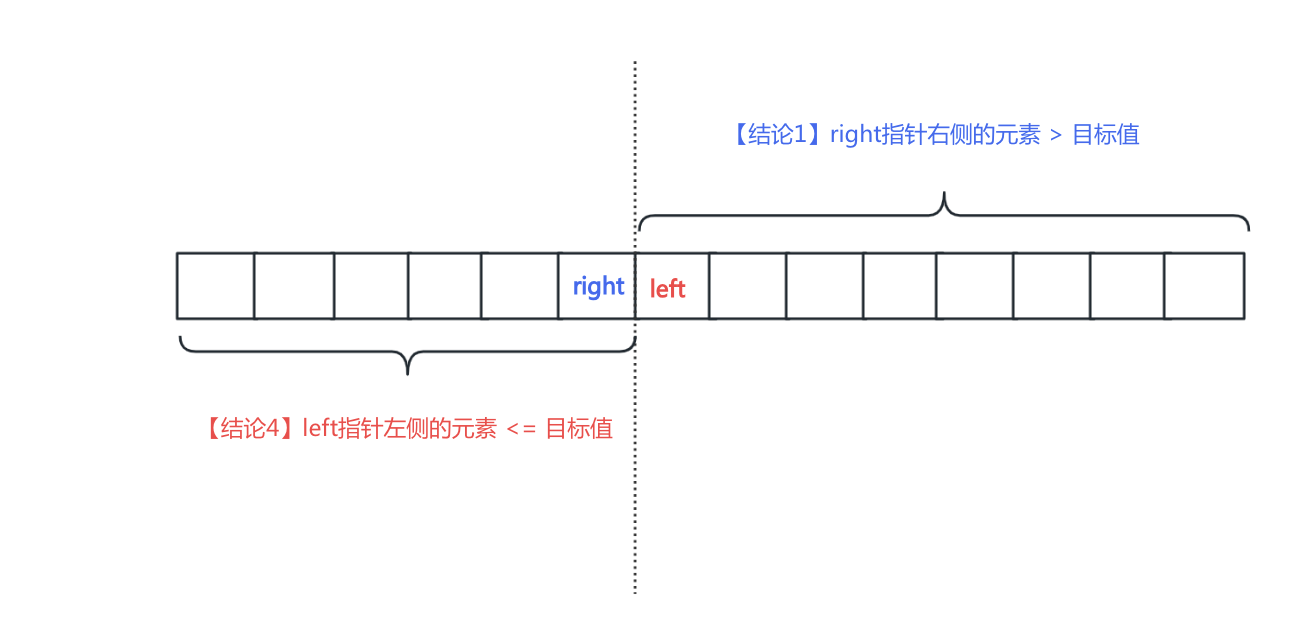
结论1：right指针右侧的元素（不包含right指针指向的元素）一定是大于目标值
结论2：left指针左侧的元素（不包含left指针指向的元素）一定是小于目标值

这里，由于需要寻找元素最后一次出现的位置。故当nums[mid]与目标值相等时，我们依然需要继续搜索右区间（显然是更新left指针为mid+1）。因为此时mid所指向的位置并不一定是该元素最后一次出现的位置，关于这一点也很好理解

但此时需要注意，当nums[mid]与目标值相等时，我们会继续搜索右区间。这样其实会导致原有结论2发生变化，即：

结论4：left指针左侧的元素（不包含left指针指向的元素）一定是 小于等于 目标值

由于循环条件为 left <= right。故当整个二分查找的循环结束后，必定有right+1=left。结合结论1、结论4，结合下图。我们知道如果这个有序数组中存在目标值的元素。那么它最后一次出现的位置一定是left指针左侧的第一个元素，由于left-1=right。即为right指针指向的元素。但注意的是该数组中也可能不存在目标值的元素，故最后还应该对right指针指向的元素进行检验：边界检查、值检查

/**
 * 寻找元素重复出现时的最后一个位置(即，右下标)
 * @param nums 存在重复元素的有序数组
 * @param target 目标元素值
 * @return
 */
private int findRightIndex(int[] nums, int target) {
    int left = 0;
    int right = nums.length-1;
    while (left<=right) {
        int mid = left + (right-left)/2;
        if ( target<nums[mid] ) {
            // 目标元素在左侧区间, 即 [left, mid-1]
            // 故更新right值
            right = mid-1;
        } else if ( target>nums[mid] ) {
            // 目标元素在右侧区间, 即 [mid+1, right]
            // 故更新left值
            left = mid+1;
        } else if( target==nums[mid] ) {
            // 在找到目标值后继续寻找右边界, 需要继续搜索右区间
            // 故更新left值
            left = mid+1;
        }
    }

    // 边界检查、值检查: 防止查找元素不存在
    if ( right>=0 && right<nums.length && nums[right] == target ) {
        return right;
    } else {
        // 元素不存在
        return -1;
    }
}

总结

针对存在重复元素的二分查找问题，当nums[mid]与目标值相等时，我们是向左搜索、还是向右搜索。这个根据需要查找的位置是第一次、还是最后一次，还是比较容易、快速思考、判断出来的。但关键的问题在于：

最终我们是取left指针指向的元素、还是取right指针指向的元素？我们如何进行思考呢？

通过上述对结论3、结论4的分析、推理过程，我们不难看出关键的问题在于：

我们不需要关心[left、right]区间中的元素具有何种性质！我们应该关心区间外的元素（即：left指针左侧的元素、right指针右侧的元素）具有何种性质！

同时，结合循环结束后两个指针的关系：right+1=left。就可以比较容易的判断出是取left指针指向的元素、还是取right指针指向的元素了

xyZGHio

浅谈二分查找问题