本文介绍在常数空间复杂度下找出数组中多数元素的Boyer–Moore摩尔投票算法

楔子

找出数组中的多数元素：对于一个含N个元素的的无序数组，请找出该数组中出现的多数元素。其中多数元素指的是出现的次数超过一半以上的元素。并假设该数组中一定存在多数元素

对于该问题，最朴素的思路就是遍历数组中的各元素并进行计数，显然该思路下时间、空间复杂度均为线性。而Boyer–Moore摩尔投票算法则可以进一步的将空间复杂度降到常数级别

基本原理

在Boyer–Moore摩尔投票算法中，其维护了两个变量：major多数元素、vote投票数。然后开始遍历数组：

如果投票数为0时，则将数组中的当前元素作为major多数元素
如果数组中的当前元素与major多数元素相同，则票数+1；反之减1

遍历结束后，如果该数组中存在多数元素，则major变量返回的一定是多数元素

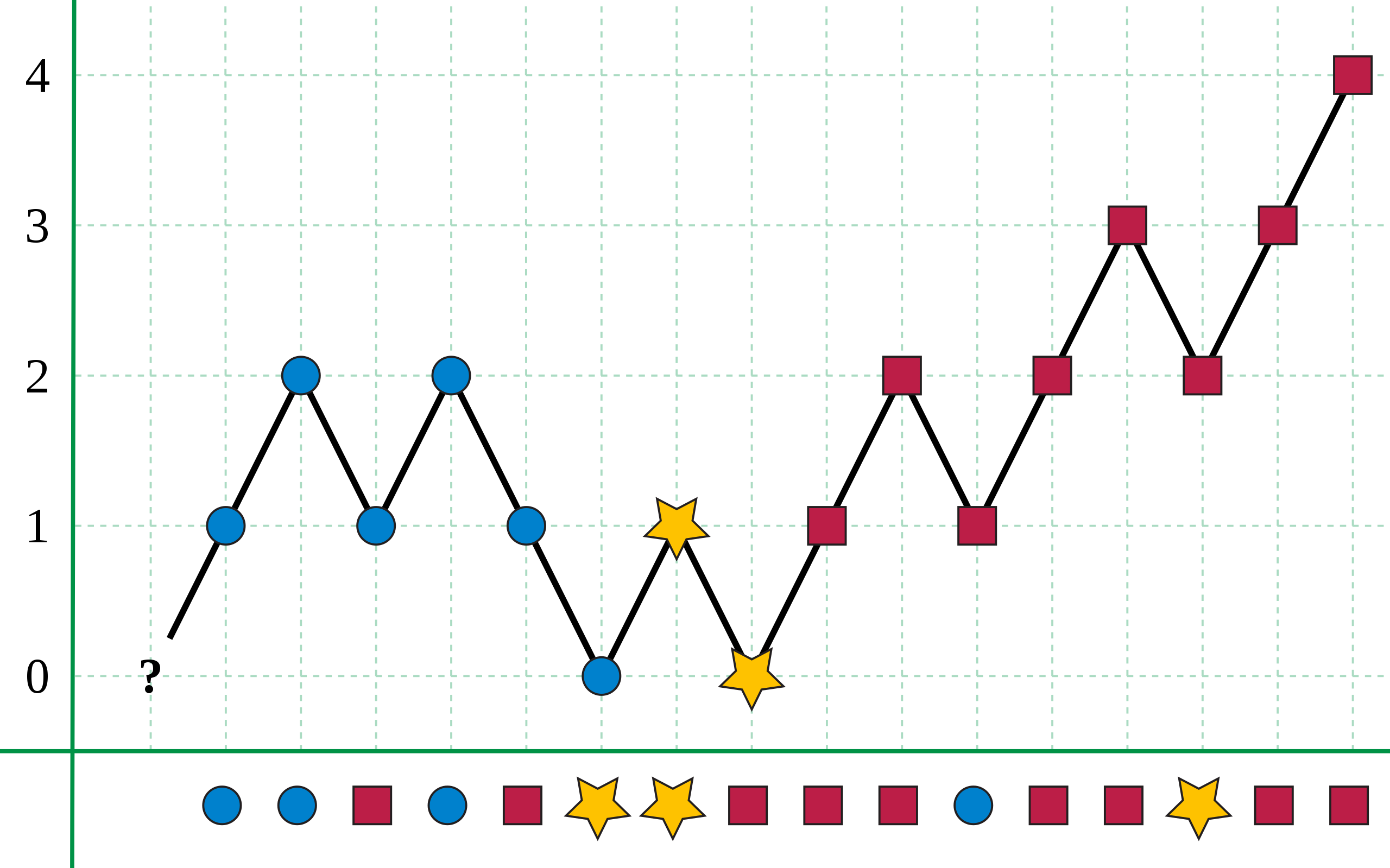
该算法的理解其实非常简单：在一个多方互相打仗的游戏中，每个己方士兵和对方一个士兵打仗的结局都是一对一同归于尽，则最后还有存活士兵的一方即为胜利方。假设你方士兵数超过总士兵数一半以上，最差的情况下，其他国家的所有士兵都联合起来对付你（即每次都是选择多数元素作为major变量的值）；当然其他国家之间也可能会相互攻击（即选择不是多数元素的元素作为major变量的值）。但只要你方士兵内部不要发生内斗、相互对拼消耗，则最后肯定是你方获胜

值得一提的是，之前我们假设了数组中一定存在多数元素，则此时Boyer–Moore摩尔投票算法给出的结果一定是多数元素。但对于一个可能不存在多数元素的数组而言，则需要对该算法给出的结果做进一步检查。具体地，遍历原数组对算法结果进行计数，检查其出现次数是否超过半数以上

实现

这里给出Boyer–Moore摩尔投票算法在Java下的实现，并对数组中可能不存在多数元素的场景进行检验

/**
 * Boyer–Moore摩尔投票算法
 */
class Solution {
    public int majorityElement(int[] nums) {
        Integer major = null;  // 多数元素
        Integer vote = 0;   // 投票数

        for (Integer num : nums) {
            // 票数为0, 直接将当前元素作为多数元素
            if(vote == 0) {
                major = num;
            }
            // 当前元素与多数元素相等, 则票数加1
            if(num.equals(major)) {
                vote++;
            } else {    // 当前元素与多数元素不等, 则票数减1
                vote--;
            }
        }
        
        // 对摩尔投票算法结果进行检查
        int count = 0;
        for(Integer num : nums) {
            if( num.equals(major) ) {
                // 对算法结果进行计数
                count++;
            }
        }
        if( count <= nums.length/2  ) {
            // 算法结果 不符合多数元素半数以上的要求
            major = null;
        }
        return major;
    }
}