生成函数,又称作母函数。作为组合数学中的一个重要理论、工具。这里介绍其中的EGF指数生成函数

EGF指数生成函数
概述
对于数列{a0,a1,a2,a3,…,an}来说,如果我们期望找出对应的普通生成函数。可能该普通生成函数的性质会比较复杂。反之,我们如果转而研究数列{a0/0!,a1/1!,a2/2!,a3/3!,…,an/n!},则可能会得到一个相对简单的生成函数。则我们可以通过如下方法将数列a与函数建立联系
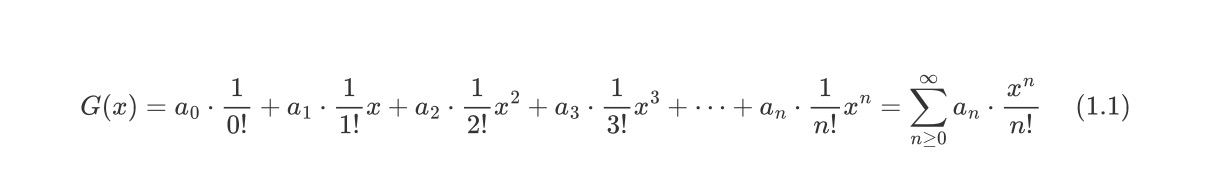
这里,我们称G(x)是数列a的指数生成函数。当然换个角度想,将G(x)理解为是数列{an/n!}的普通生成函数,自然也是正确的。需要强调的是,在生成函数中,对于自变量x,其只是一个形式而已。我们不关心x的取值和级数是否收敛。因为我们关心的是生成函数中各项的系数
运算性质
微分
令数列{a0,a1,a2,a3,…,an}的指数生成函数为G(x),则我们对其微分后有
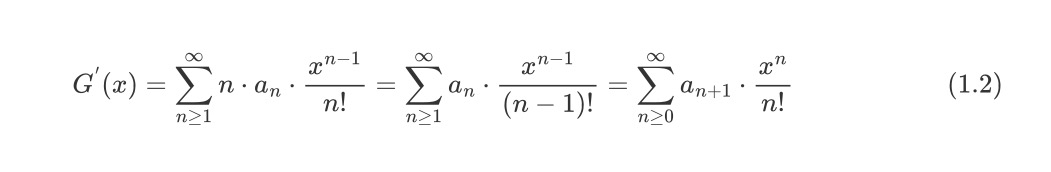
不难看出,微分后的结果是数列{a1,a2,a3,…,an}的指数生成函数。即指数生成函数的微分操作与普通生成函数的左移一位操作是相对应的
积分
令数列{a0,a1,a2,a3,…,an}的指数生成函数为G(x),则我们对其变上限定积分,则有
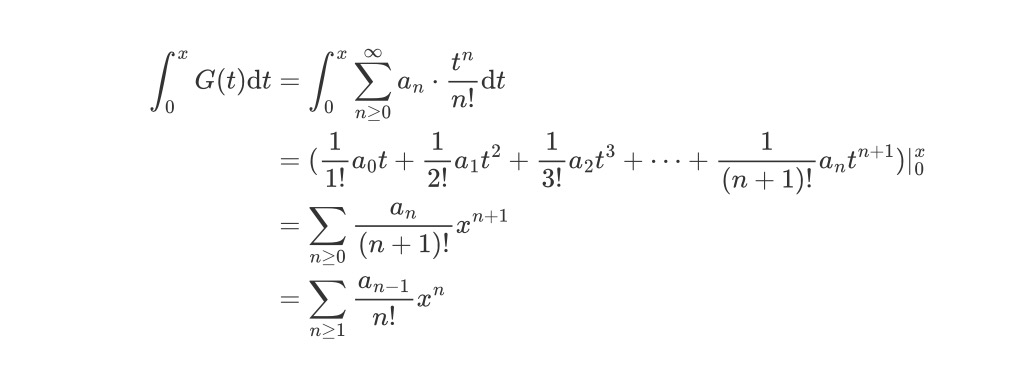
不难看出,积分后的结果是数列{0,a1,a2,a3,…,an}的指数生成函数。即指数生成函数的积分操作与普通生成函数的右移一位操作是相对应的
卷积
令数列a,b的指数生成函数,分别为F(x)、G(x),则有:

即,F(x)G(x)是数列
的指数生成函数
封闭形式
在实际使用生成函数的过程中,我们不会一直使用形式级数的形式。而是更多的使用其封闭形式以更好地计算。下面给出常见数列对应的指数生成函数及其相应的封闭形式。事实上不难看出,将EGF的的封闭形式展开为麦克劳林级数(即在x=0处的泰勒展开),就是我们上面见到的形式级数样子了
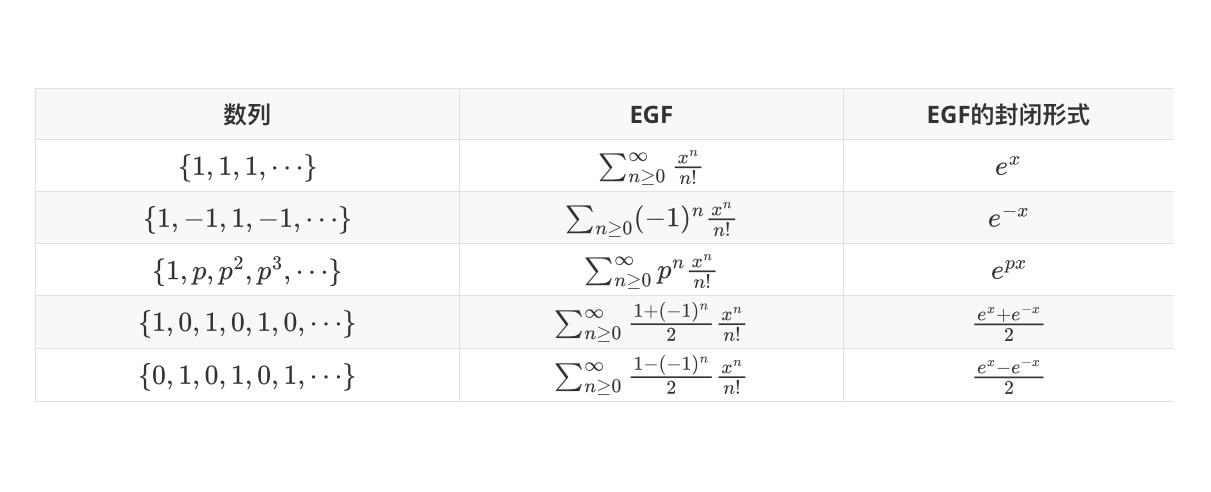
多重集的排列问题
全排列
对于一般的集合而言,某个元素要么不出现,要么只能出现一次。而在多重集中其包含k种不同的元素。但对于同一个种类的元素而言,其在多重集中是允许重复出现的。例如:S={a,a,b,b,b,c}。在多重集S中存在3种不同的元素,分别是a、b、c,并且有2个a元素、3个b元素、1个c元素

事实上,我们对结果进行观察,直观上也很好理解。分子即为n个元素的全排列,分母则是分别对k种元素相同的排列进行去重
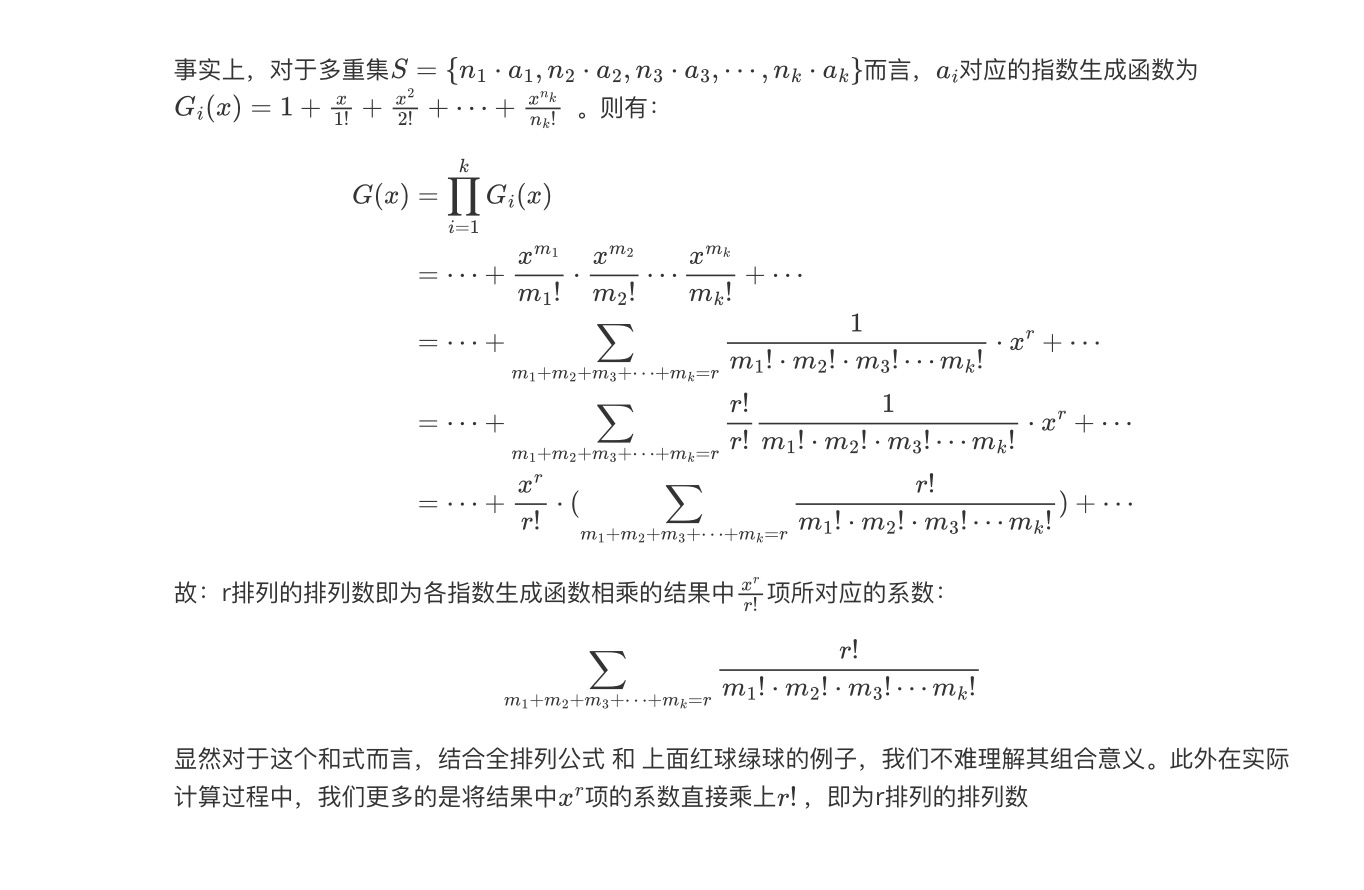
r排列
从包含n个元素的多重集中选取 r 个元素进行排列。当r=n时即为全排列,上面已经讨论过了,现在我们来看下r<n时的情形。我们先来看一个简单点的例子。假设这里有2个红球、3个绿球,试问如果从这5个球中取出2个球,有多少种排列?

格子涂色问题
假设一行中有N个方块,每个方块都可以涂成红色、蓝色、绿色或黄色。由于某种原因,老王希望红色块、绿色块的数量均是偶数。试问在这种情况下,老王给N个方块涂色的方法数
本题显然是一道多重集的排列问题。其中,蓝色块、黄色块使用数量无限制,而红色块、绿色块则分别要求是偶数个(显然0个也是偶数个),现在我们用指数生成函数来解该题

参考文献
- 具体数学·第2版 Ronald L.Graham、Oren Patashnik、Donald E.Knuth著
