统计学分两大类:描述统计学和推断统计学。前者是通过指标参数(比如,平均数,四分位数,标准差等)描述和研究数据集的整体情况;后者则主要研究如何利用样本数据集来推断总体数据特征。而推断统计学中的假设检验: 即是指在一定的假设条件下根据样本来推断总体特征。本文将对假设检验中的基本理论做介绍

基本原理
我们首先需提出一个我们期望证实的假设(Hypothesis ),记为$H_1$假设。但是现实中很多情况下,我们很难直接证明$H_1$假设的真伪性。故,我们从$H_1$假设的反面提出一个新的假设——$H_0$假设。由此将对$H_1$假设的真伪判定转换为对$H_0$假设的真伪判定。如果有把握证明$H_0$假设是假,则$H_1$假设得证;若没有把握证明$H_0$假设是假,则说明$H_1$假设不能被接受
我们一般把$H_0$假设称作虚无假设(Null hypothesis) ,亦或叫作零假设、原假设。笔者更倾向于称之为虚无假设,因为该假设是我们为了方便检验$H_1$假设而提出的,且期望虚无假设$H_0$能够被证伪;而把$H_1$假设称之为备择假设(Alternative hypothesis) ,亦或叫作对立假设,该假设是我们期望证实的假设,一旦虚无假设$H_0$被证伪拒绝,则该假设即被备你选择,被你接受
说到这里,可能有的朋友会发现,假设检验的思想和数学中的反证法很类似。但其实际上又有所区别,后者是在假设某一条件时发生了不合理的现象——逻辑的矛盾,从而否定该假设的条件,从而使得原条件得证。而假设检验中的不合理现象的推断依据是小概率原理:
小概率原理是指一个事件的发生概率很小,那么它在一次试验中是几乎不可能发生的,但在多次重复试验中是必然发生的。统计学上,把小概率事件在一次实验中看成是实际不可能发生的事件,一般认为等于或小于0.05或0.01的概率为小概率
检验假设时,我们首先根据实际场景的需要,确定出判定小概率事件的概率阈值,通常取0.05(即5%),记为$\alpha = 5\%$,在假设检验中,$\alpha$被称作为显著性水平。在$H_0$假设条件下,计算出现给定样本数据的发生概率,此概率即为统计学中常常见到的p值(p-value)
- 当 $p \leq \alpha$ 时,说明在$H_0$假设条件下,出现给定的样本数据是一个小概率事件,而实际上样本数据确实如此,即发生了不合理现象。故认为$H_0$假设是错误的、被证伪。从而,拒绝$H_0$假设,接受$H_1$假设
- 当 $p > \alpha$ 时,说明在$H_0$假设条件下,出现给定的样本数据不是一个小概率事件,出现给定的样本数据是合理的,故$H_0$假设被接受,而$H_1$假设被拒绝
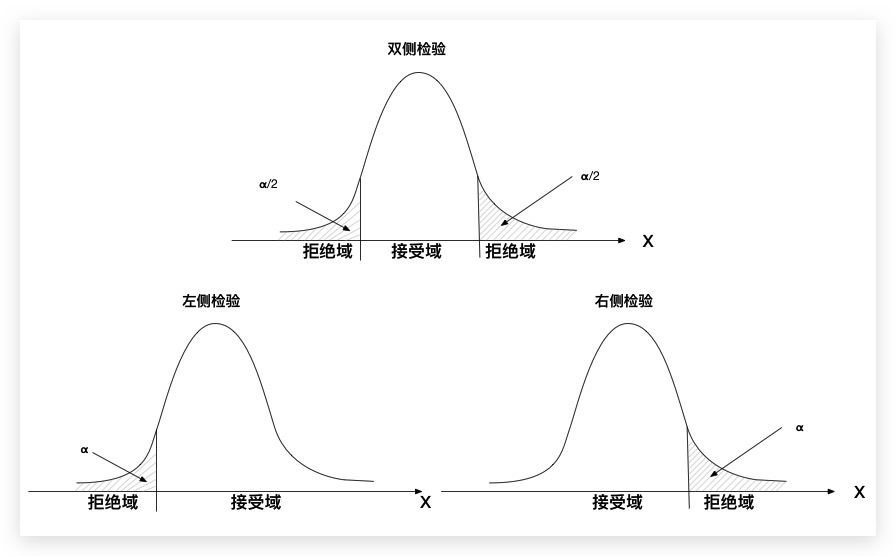
具体的校验过程中,又可分为 单侧校验(左侧、右侧) 和 双侧校验 ,如下所示。如果所给样本数据X落在拒绝域中,即可拒绝$H_0$假设,接受$H_1$假设;反之则接受$H_0$假设,拒绝$H_1$假设
小试牛刀
现以《程序员的数学2·概率统计》一书中的例题为例,来展示假设检验的具体过程
假设甲乙两人共比赛100次,其中甲61胜39败。下面是他们对该结果的争论
甲: 我比你更强
乙: 不,这纯属偶然
甲: 偶然?那也差距太大了吧!这明显是我们的实力差距
乙: 也不一定吧,就算实力差不多,偶尔出现这样的结果也不奇怪吧?
甲: 没那种事
乙: 真的吗?你具体计算一下试试?
甲: 好,我现在就算。如果出现现在这个结果(甲61胜39败)的概率小于5%,你就承认这是实力的差距吧
通过一次比赛结果来判断总体的实力水平,就可以通过假设检验来进行推断。甲认为自己的比赛水平高于乙,故,可以提出如下的备择假设:
$H_1$: 甲获胜的概率 > 1/2
我们无法直接对我们期望证实的$H_1$假设来进行判定,所以,我们需要提出一个虚无假设来进行判定推断
$H_0$: 甲获胜的概率 = 1/2
上述场景中的5%,即为我们根据实际需要来设定的显著性水平$\alpha$
根据虚无假设$H_0$的条件,计算出现上述比赛结果的概率,易知100次比赛中甲获胜X次数的概率符合二项分布: $X \sim B(100,1/2)$
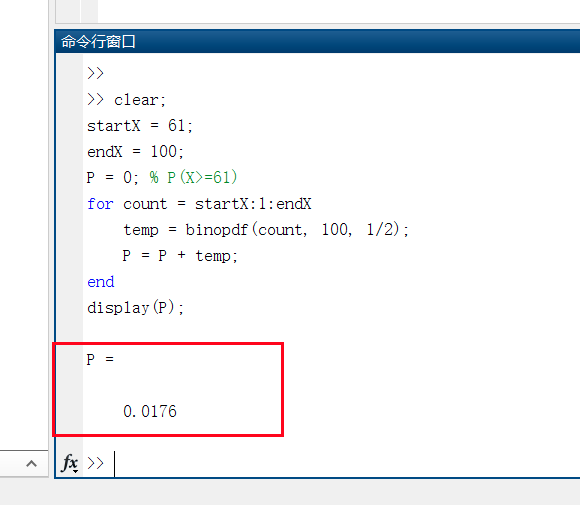
这里利用Matlab计算可得: $P(X\geq 61) = 0.0176 < \alpha = 5\%$,故我们知道在$H_0$虚无假设下,出现当前比赛结果的概率远低于我们之前设定的显著性水平$\alpha = 0.05$,即在$H_0$假设下,出现当前比赛结果是一个小概率事件,而实际样本数据即是这样的,故发生了不合理现象,所以,我们拒绝了虚无假设$H_0$,接受了备择假设$H_1$,即,出现这样的比分结果,是由于甲的实力水平高于乙,而不是偶尔恰好发生的
假设检验的两类错误
从上面的例子中,我们基本了解了假设检验的具体过程和实施步骤。在这个例子中,我们所取的显著性水平$\alpha$ 为5%,而如果我们选用1%的显著性水平,则我们最终的结果将于上题的结论完全相反,即, $P(X\geq 61) = 0.0176 > \alpha$,接受$H_0$虚无假设,拒绝$H_1$备择假设。可以看出,选用不同的显著性水平$\alpha$,将会大大影响假设检验的最终结果,也就是说假设检验的推断结果,不是百分之百的正确,而是有一定的犯错概率。在假设检验中的存在两类错误:
- Ⅰ型错误: 当虚无假设$H_0$实际上是正确的,我们却错误地拒绝了它。又叫作第一类错误、$\alpha$错误
- Ⅱ型错误: 当虚无假设$H_0$实际上是错误的,我们却错误地接受了它。又叫作第二类错误、$\beta$错误
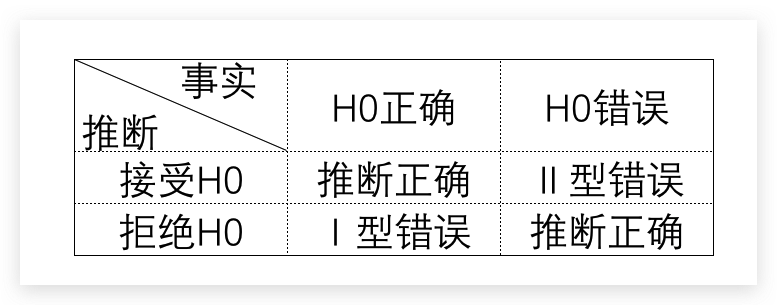
如上文所述,在假设检验中,当p值(p-value)小于显著性水平$\alpha$时,即会拒绝虚无假设$H_0$。所以,Ⅰ型错误的发生概率即为显著性水平$\alpha$
