本文介绍非确定有限状态自动机NFA的基本原理,并结合具体示例进行实践

基本原理
对于NFA非确定有限状态自动机A而言,其通常包含以下几个元素:
- 非空有限的状态集合 Q
- 非空有限的输入集合 ∑
- 转换函数 𝜹: Q x ∑ -> P(Q),其决定了当前状态在某输入的作用下允许进入的下一个状态集合。其中P(Q)意为Q的幂集
- 初始状态 s∈Q
- 可接受状态集合 F⊆Q。其表明当输入结束时,自动机所处状态为合法状态的集合
通过上面的转换函数定义,其实不难看出非确定有限状态自动机NFA与确定有限状态自动机DFA的区别。对于NFA而言,从当前状态进入下一个状态时并不是确定的,其可能会允许进入多个状态,即所谓的多个分支。这样当NFA在工作时,如果选择某个分支一直走下去,当输入完全遍历完后发现自动机并不是处于可接受的状态时,我们并不能立即判定为失败。因为自动机还需要依次回溯选择其它状态分支继续尝试走下去,直到自动机遍历完全部的状态分支发现最终依然无法处于可接受状态时,我们才可以判定为失败。反之,如果自动机一旦在某个状态分支遍历过程中,当输入完全遍历完后发现自动机正好处于可接受的状态时,我们就可以直接判定为成功。显然这一过程非常类似于深度优先搜索DFS
而NFA-𝜖则是在NFA的基础上作进一步推广,最大的区别就在于其允许存在𝜖转换。我们知道对于自动机而言,从状态A到状态B的转换过程上需要消耗一个输入符号。而𝜖转换则是不消耗输入符号,即所谓的空转换。故对于NFA-𝜖而言,其转换函数如下所示
利用𝜖转换可以很方便地使系统能够处于多种状态中,提供了一种模糊建模的方式。典型地,这里我们以正则表达式为例,展示如何通过NFA-𝜖进行表示
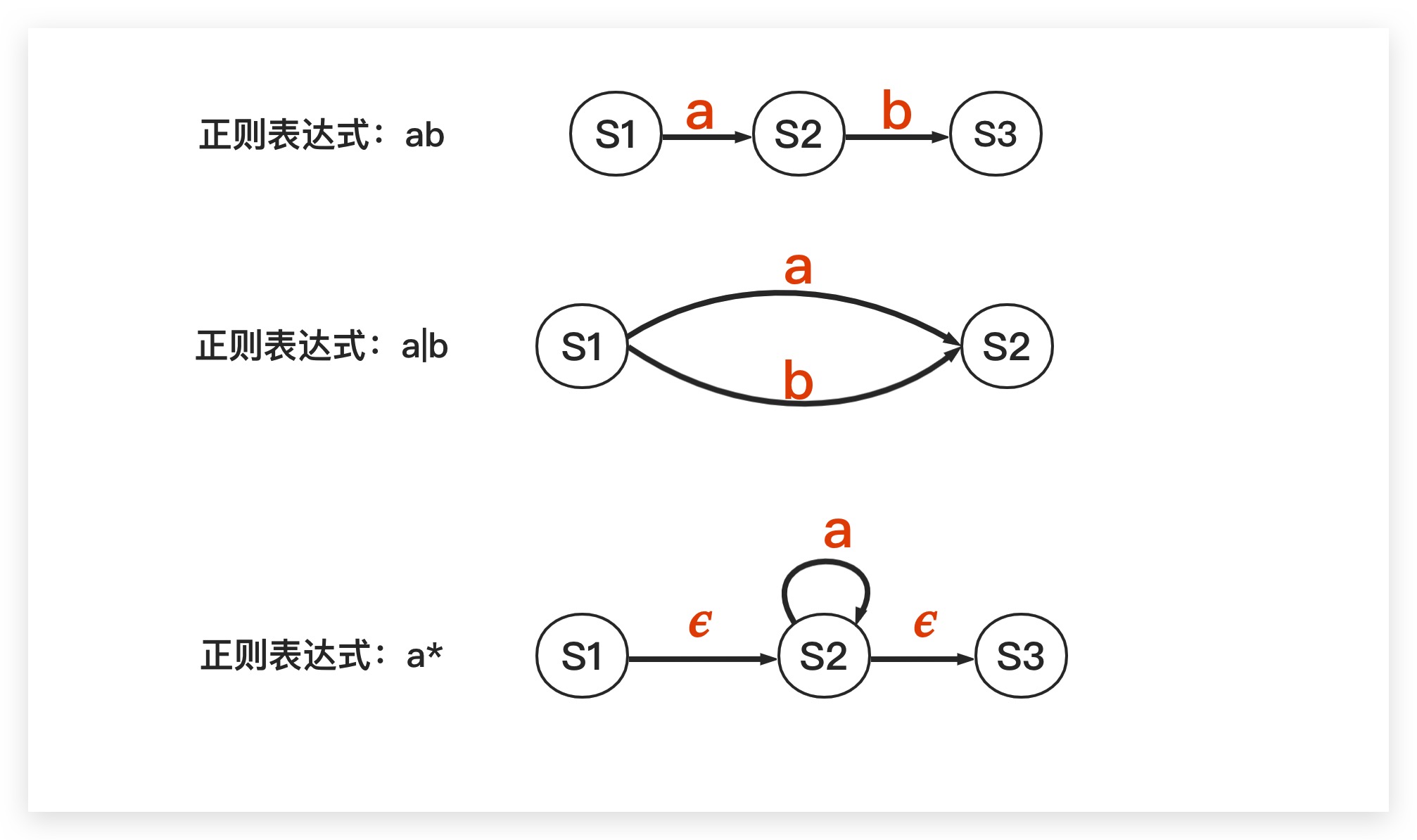
实践
学习过程中要善于理论联系实际。故在介绍完NFA的基本原理后,现在我们来进行实践。这里以LeetCode的第10题——正则表达式匹配为例
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 . 和 * 的正则表达式匹配
. :表示匹配任意单个字符
* :表示它前面的字符可以出现任意次(含0次)
所谓匹配是要涵盖整个字符串s的,而不是部分字符串
输入:s = “aa”, p = “a”
输出:false
解释:a无法匹配aa整个字符串
输入:s = “aa”, p =”a*“
输出:true
解释:因为 * 代表可以匹配零个或多个前面的那一个字符, 在这里前面的字符就是a。因此,字符串aa可被视为a重复了一次
输入:s = “ab”, p =”.*“
输出:true
解释:.* 表示可匹配零个或多个(*)任意字符(.)
从题目中不难看出,对于 . 符号而言,还是比较好处理的,把它当作一个普通的万能字符进行匹配即可。而对于 * 符号而言,我们则需要进行特殊处理。具体地,对于给定的正则表达式ab*c我们尝试将其转换为NFA-𝜖进行。首先,根据上文内容,我们可以很快分别给出a、b*、c这三个部分的自动机表示,然后通过𝜖转换将三部分串联起来,最后合并消去不必要的𝜖转换转换即可。如下图所示
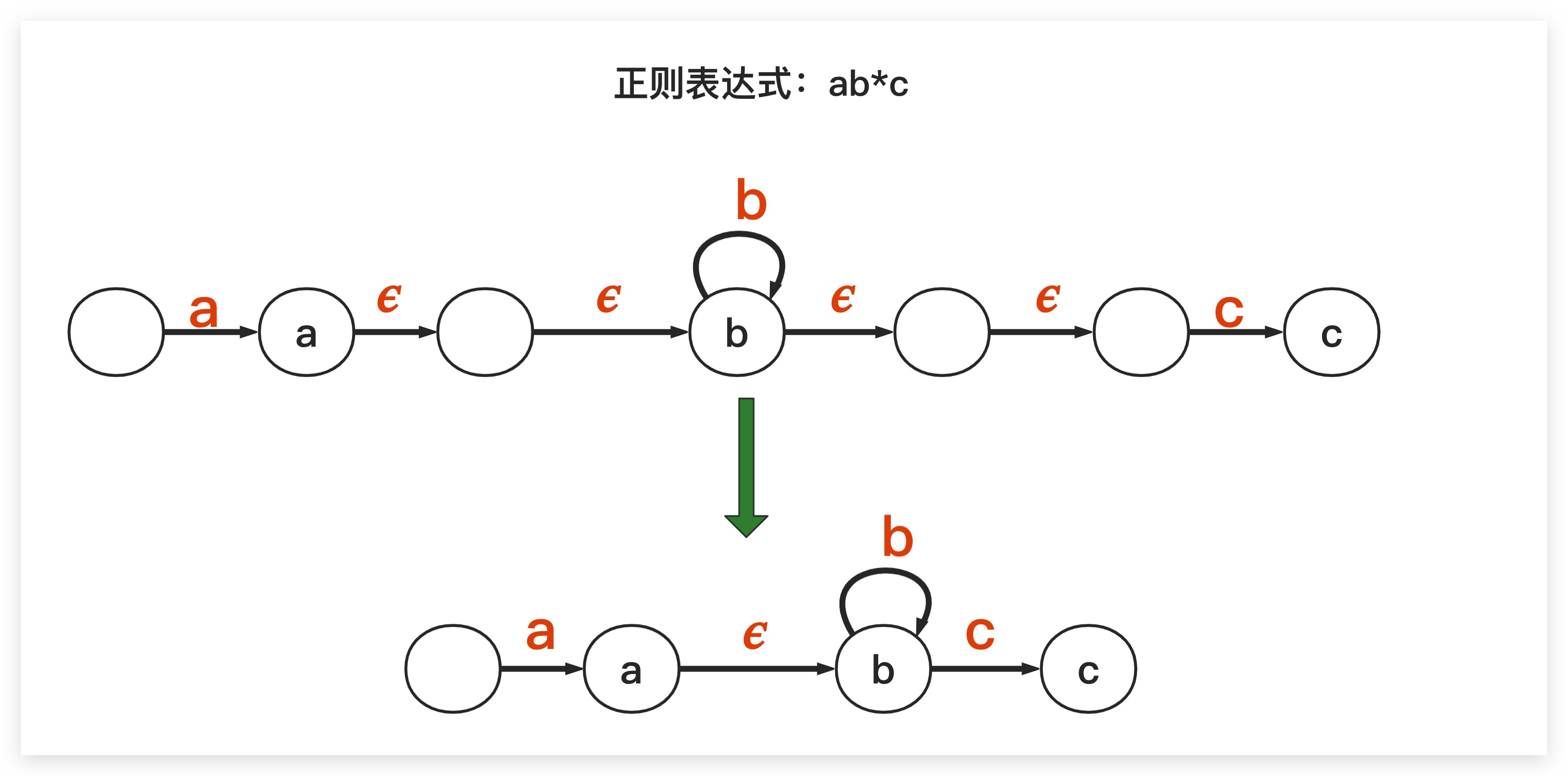
观察上图的自动机不难发现,如果正则表达式中存在b*部分,则一方面到达b状态是通过𝜖转换即空转移实现的,另一方面可通过重复b字符再次进入当前状态。这里给出Java下的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
class Solution {
private List<Character> state;
private Set<Integer> repeatSet;
private Set<Integer> epsilonSet;
public boolean isMatch(String s, String p) {
if( s==null || s=="" || p==null || p=="" ) {
return false;
}
state = new ArrayList<>();
repeatSet = new HashSet<>();
epsilonSet = new HashSet<>();
int index = -1;
for(char ch : p.toCharArray()) {
if( (ch>='a' && ch<='z') || ch=='.' ) {
state.add(ch);
index++;
} else if( ch=='*' ) {
repeatSet.add( index );
epsilonSet.add( index);
}
}
boolean res = dfs(s.toCharArray(), -1, -1,0);
return res;
}
private boolean dfs(char[] chars, int charsIndex, int stateIndex, int opsType) {
if( charsIndex > chars.length-1 && stateIndex > state.size()-1 ) {
return true;
}
if( charsIndex > chars.length-1 || stateIndex > state.size()-1 ) {
return false;
}
if( opsType==1 ) {
if( !epsilonSet.contains(stateIndex) ) {
return false;
}
} else if ( opsType==2 ) {
if( epsilonSet.contains(stateIndex) ) {
return false;
}
if( chars[charsIndex]!=state.get(stateIndex) && state.get(stateIndex)!='.' ) {
return false;
}
} else if( opsType==3 ) {
if( !repeatSet.contains(stateIndex) ) {
return false;
}
if( chars[charsIndex]!=state.get(stateIndex) && state.get(stateIndex)!='.' ) {
return false;
}
}
return dfs(chars, charsIndex, stateIndex+1, 1)
|| dfs(chars, charsIndex+1, stateIndex+1, 2)
|| dfs(chars, charsIndex+1, stateIndex, 3);
}
}
|



