生成函数,又称作母函数。作为组合数学中的一个重要理论、工具。这里介绍其中的OGF普通生成函数

OGF普通生成函数
概述
对于任意数列{a0,a1,a2,a3,…,an},我们可以通过如下方法将其与函数建立联系
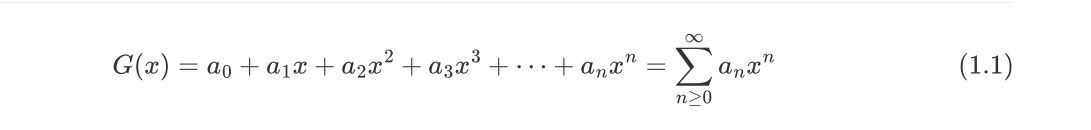
则我们说G(x)是数列a的生成函数。这里的G(x)就是OGF普通生成函数,其本质就是一个形式幂级数。需要强调的是,在生成函数中,对于自变量x,其只是一个形式而已。我们不关心x的取值和级数是否收敛。因为我们关心的是生成函数中各项的系数
运算性质
这里介绍生成函数的运算性质
线性运算
令数列a、b的普通生成函数,分别为F(x)、G(x),则有:
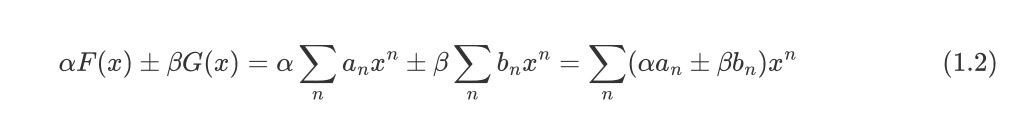
即𝛼F(x)±𝛽G(x)是数列{𝛼a±𝛽b}的普通生成函数
卷积运算
令数列a,b的普通生成函数,分别为F(x)、G(x),则有:
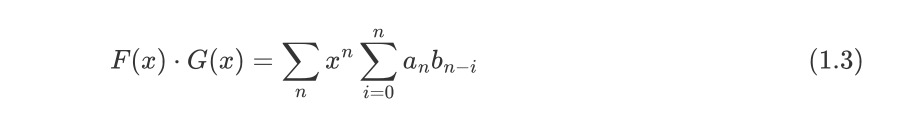
即F(x)G(x)是数列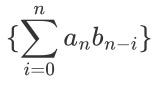
的普通生成函数
向右/左平移m位
令数列a的普通生成函数为G(x)。现将数列{a1,a2,a3,…,an}向右平移m位,则变成前m项为0的数列 {0,0,0,…0,a1,a2,a3,…,an},则有:
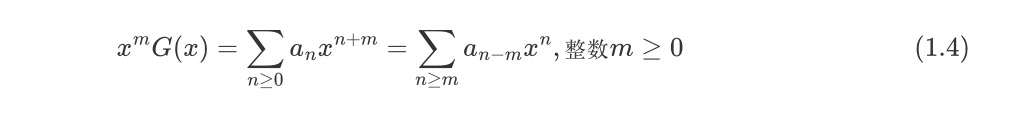
令数列b的普通生成函数为F(x)。现将数列{b1,b2,b3,…,bn}向左平移m位,则变成数列 {bm,…,bn},则有:
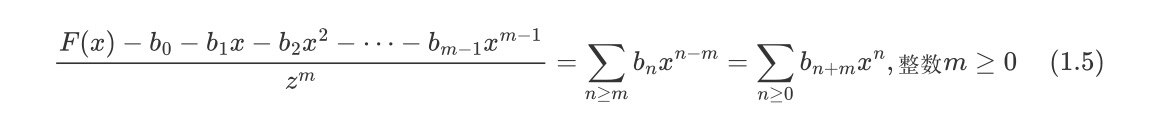
微分
借助微分操作,则可以实现将n放到系数当中。如下所示
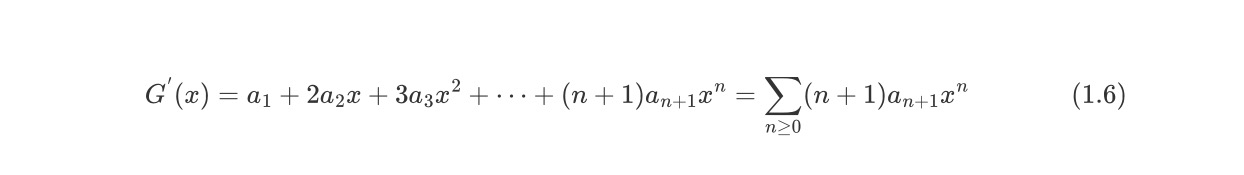
事实上,对于微分后的结果,我们向右平移1位,即可得到下面的结果
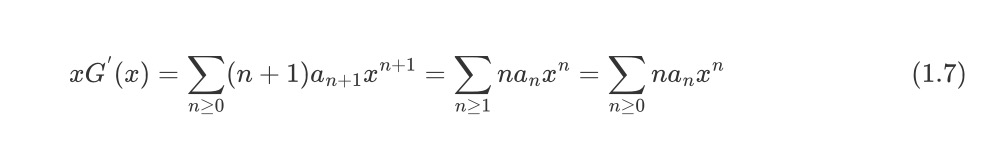
积分
我们对生成函数G(x)进行变上限定积分,则有
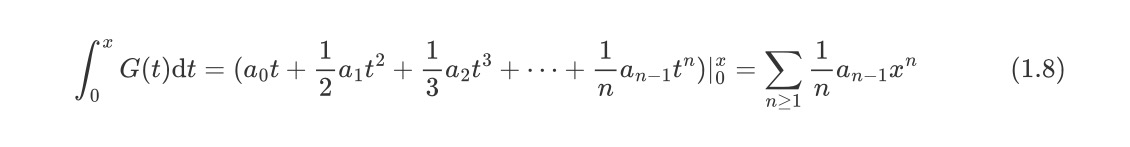
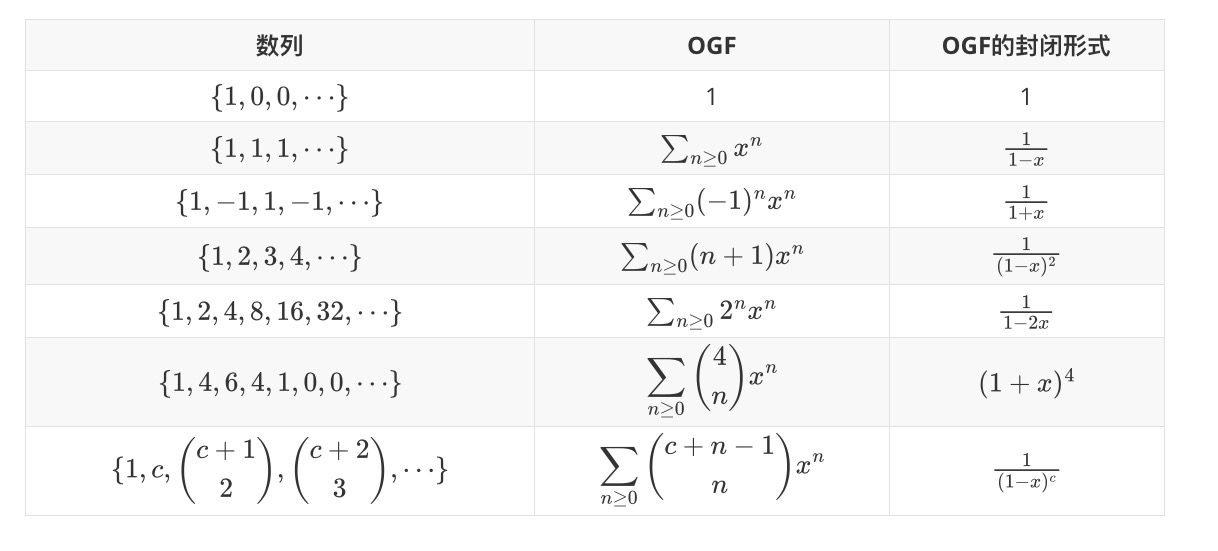
封闭形式
在实际使用生成函数的过程中,我们不会一直使用形式幂级数的形式。而是更多的使用其封闭形式以更好地计算。下面给出常见数列对应的生成函数及其相应的封闭形式。事实上不难看出,将OGF的的封闭形式展开为麦克劳林级数(即在x=0处的泰勒展开),就是我们上面见到的形式幂级数样子了
广义二项式定理
众所周知,二项式定理中的n为整数,即
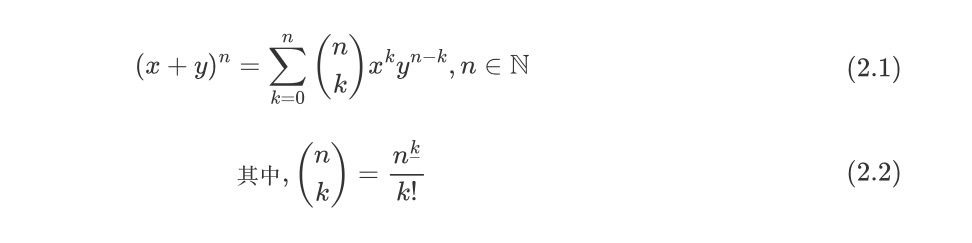
事实上,牛顿将二项式定理可以推广到任意实数次幂,即所谓的广义二项式定理。故又被称为牛顿二项式定理
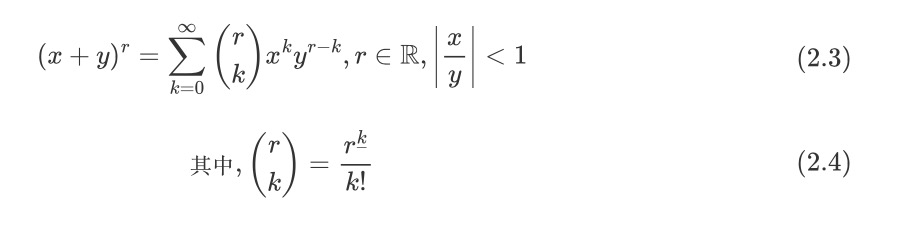
求解数列通项
生成函数的一项主要作用就是求解求数列的通项公式。基本步骤如下:
- 给出数列的递推公式,即关于an的方程
- 使用x的n次方同乘方程的两边,并对所有n进行求和。使之变为关于G(x)的方程
- 对关于G(x)的方程进行求解,求解出G(x)
- 对G(x)按幂级数展开。此时x的n次方的系数就是数列an的通项公式
斐波那契数列
现在我们来求解斐波那契数列的通项公式。第一步,给出斐波那契数列的递归公式。如下所示
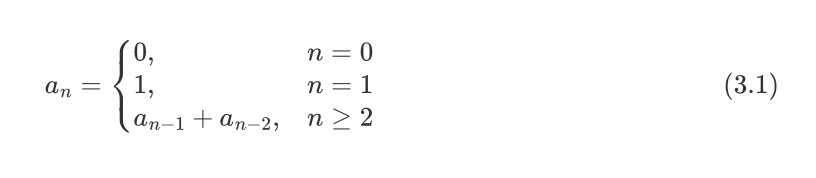
现在先使用x的n次方同乘方程的两边,然后对所有n进行求和
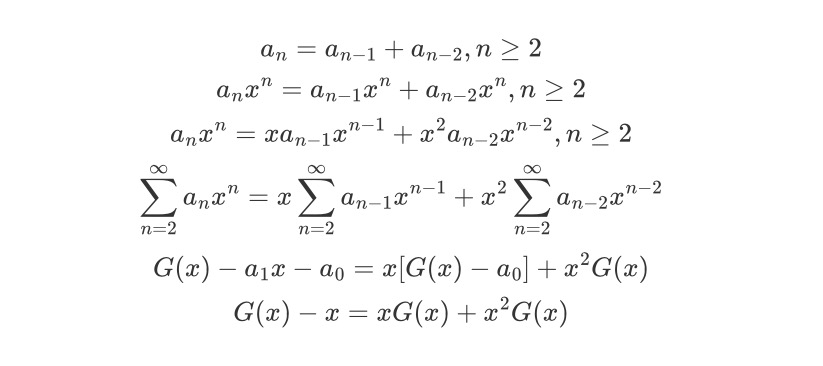
然后对关于G(x)的方程进行求解,求解出G(x)

最后,我们借助麦克劳林公式将G(x)展开为幂级数即可
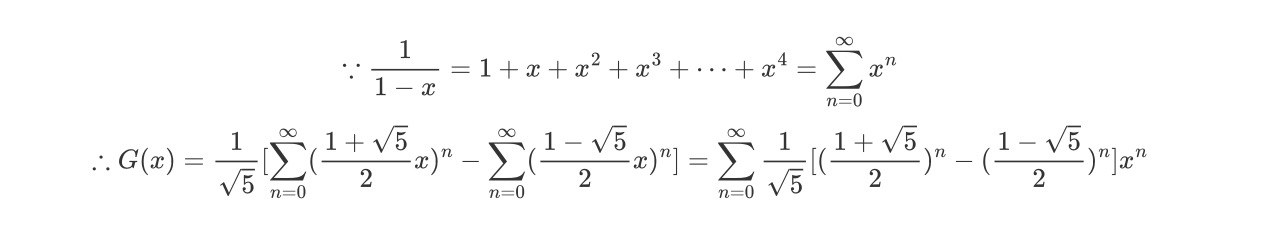
此时斐波那契数列的通项公式即为
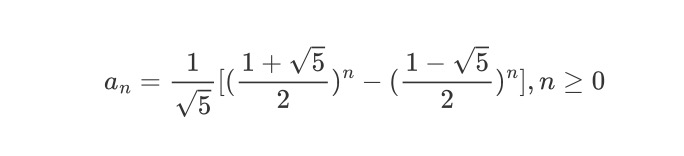
卡特兰数
现在我们来求解卡特兰数的通项公式。第一步,给出卡特兰数的递归公式。如下所示
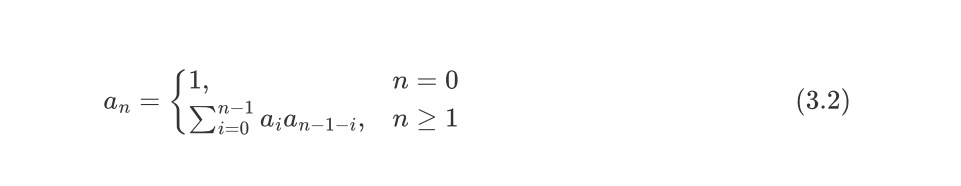
现在先使用x的n次方同乘方程的两边,然后对所有n进行求和
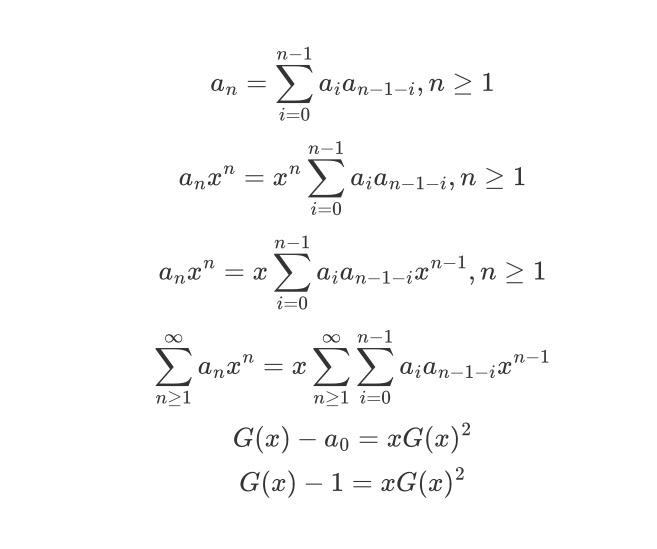
然后对关于G(x)的方程进行求解,求解出G(x)
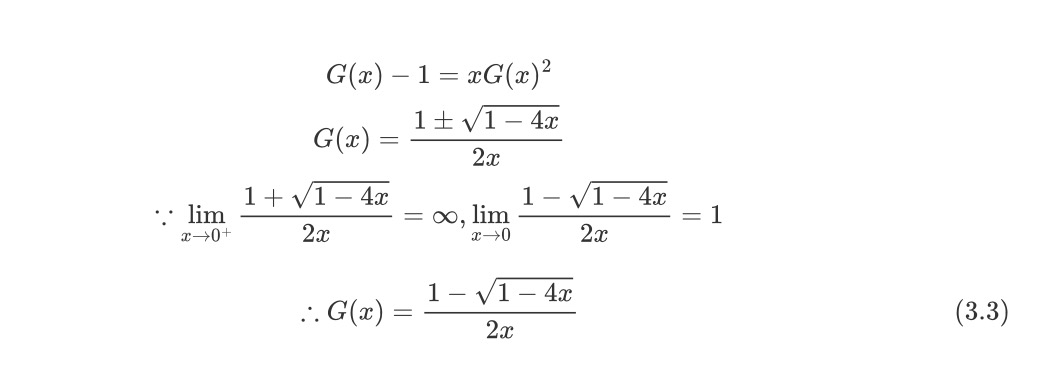
最后,我们将G(x)展开为幂级数即可。这里利用前面提到的广义二项式定理先对分子中的幂进行处理

现将上述结果带回(3.4)式得
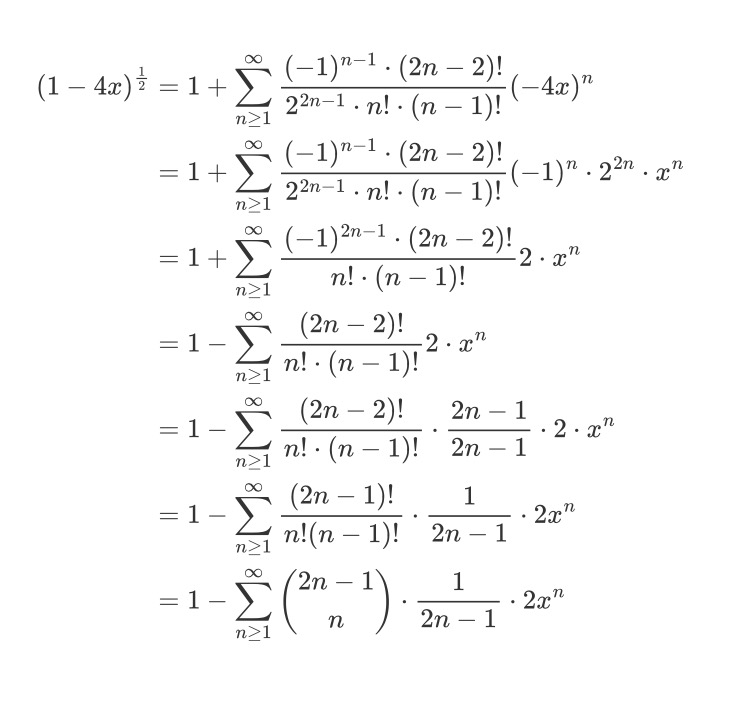
至此,我们就可以继续处理(3.3)式了
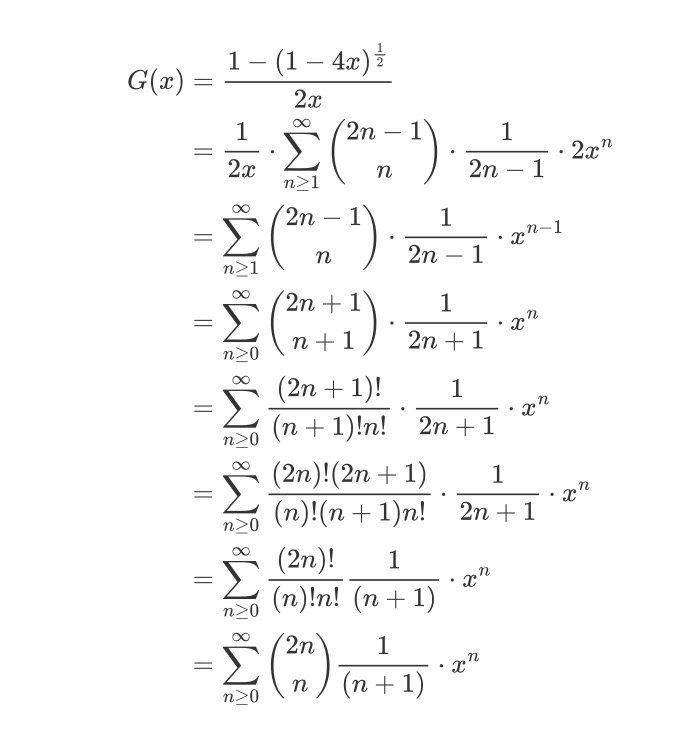
此时卡特兰数的通项公式即为
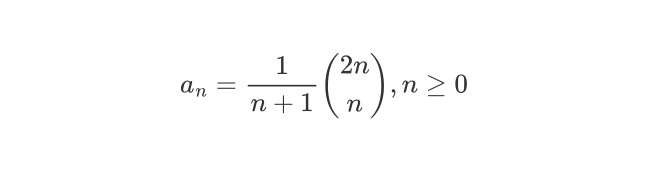
多重集的组合问题
对于一般的集合而言,某个元素要么不出现,要么只能出现一次。而在多重集中其包含k种不同的元素。但对于同一个种类的元素而言,其在多重集中是允许重复出现的。例如:S={a,a,b,b,b,c}。在多重集S中存在3种不同的元素,分别是a、b、c,并且有2个a元素、3个b元素、1个c元素
所谓多重集的组合,指的就是从一个多重集中选取指定r个的元素,不考虑排序。我们先来看一个简单点的例子。假设这里有3个◼︎、2个▲,试问如果从这5个中取出2个,有多少种组合?这里采用穷举法,其中O代表没有取
当r=0时,组合有:O。即1种
当r=1时,组合有:◼︎、▲。即2种
当r=2时,组合有:◼︎◼︎、◼︎▲、▲▲。即3种
当r=3时,组合有:◼︎◼︎◼︎、◼︎◼︎▲、◼︎▲▲。即3种
当r=4时,组合有:◼︎◼︎◼︎▲、◼︎◼︎▲▲。即2种
当r=5时,组合有:◼︎◼︎◼︎▲▲。即1种
现在我们来尝试做一点有趣的事情。对于3个◼︎而言,我们可以进行的选取操作有:O、◼︎、◼︎◼︎、◼︎◼︎◼︎,同理,对于2个▲而言,我们可以进行的选取操作有:O、▲、▲▲。现在对其进行多项式乘法,有:
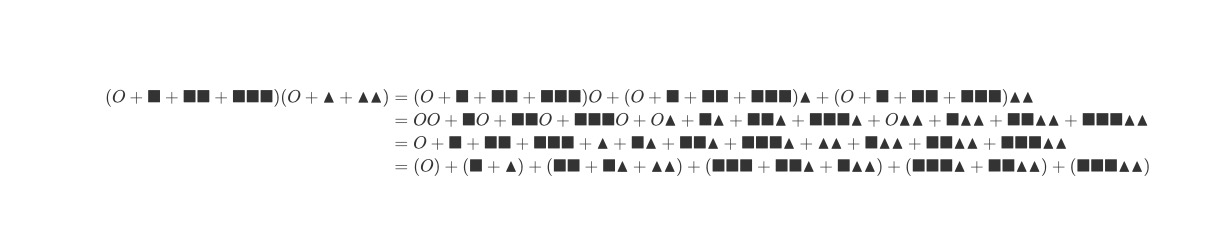
不难看出在进行所谓的多项式乘法后,其结果就是我们从这5个中任取r个的各种组合。这里我们更进一步地,将上式中形状符号替换为x。以便合并同类项。结果如下所示
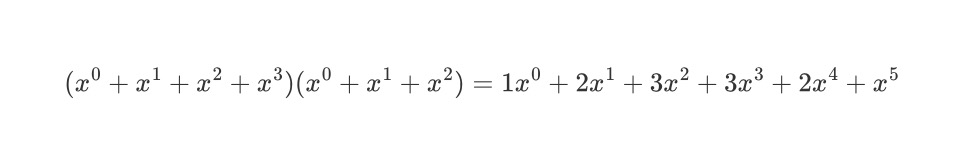
此时我们不难发现其中暗含的规律:
x的0次方的系数为:1
x的1次方的系数为:2
x的2次方的系数为:3
x的3次方的系数为:3
x的4次方的系数为:2
x的5次方的系数为:1
至此,对于多重集的组合问题,我们只需分别写出在同种类元素当中进行选取时对应的生成函数即可。其中,x的次数表示选取该类型物品的数量。而对应的系数则表示选择的组合数(事实上,这里一般都是1。道理很简单,因为选的都是同类型元素)
例如,对于3个◼︎而言,我们可以选择0个、1个、2个或3个,则对应的生成函数即为:x^0+x^1+x^2+x^3
例如,对于2个▲而言,我们可以选择0个、1个或2个,则对应的生成函数即为:x^0+x^1+x^2
然后将所有种类元素的生成函数进行多项式乘法。对于多项式乘法计算的最后结果而言,x的次数表示选取物品的总数。而对应的系数则表示选择指定数量物品的组合数。故从多重集中任取r个的组合数实际上就是,生成函数卷积后x的r次方前面所对应的系数
食物组合问题
现在我们来看一道经典问题:
老王这次要出去旅游了,他在思考他应该带一些什么东西。理所当然的,你要帮他计算携带n件物品的方案数。他这次准备带一些受欢迎的食物,如:鸡块啦,承德汉堡等等。当然,他又有一些稀奇古怪的限制。每种食物的限制如下:
- 承德汉堡:偶数个
- 可乐:0个或1个
- 鸡腿:0个,1个或2个
- 水蜜桃:奇数个(这里,如果不带则计作0个,属于偶数。故如果不带水蜜桃,则违反限制)
- 鸡块:4的倍数个
- 包子:0个,1个,2个或3个
- 土豆片炒肉:不超过1个
- 面包:3的倍数个
注意:这里我们不考虑老王对于带的食物该怎么搭配着吃。每种食物都以个为单位,只要总数加起来是n就算一种方案。因此,对于给出的N,你需要计算出方案数
这是一道经典的生成函数题。我们先表示出各类型食物选取n个的方案数的生成函数。则多种类型的食物任取n个的方案数的生成函数,就是各类型食物生成函数的卷积

故,老王携带n件物品的方案数为 (n+2)(n+1)n/6
零钱组合问题
现在你有4个1元的硬币、无穷个2元的硬币、无穷个5元的硬币。你需要支付𝑛元,请问有多少种方案?
我们先表示出各类型硬币组合为n元的方案数的生成函数。则多种类型的硬币组合为n元的方案数的生成函数,就是各类型硬币生成函数的卷积
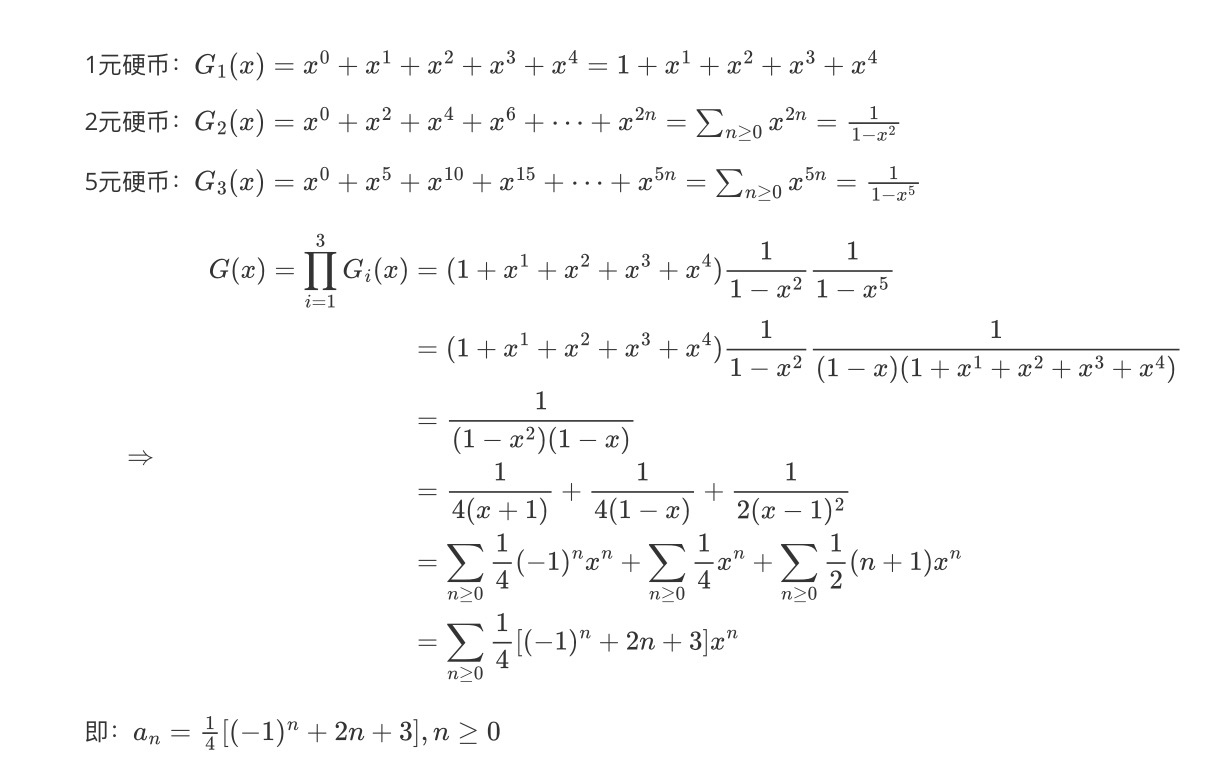
Note
- 再次特别强调,OGF中的幂级数只是形式幂级数。所以在本文中对级数进行求和时,我们并不关心它是收敛的还是发散的。实际上,即使不收敛,对于生成函数而已,相关运算也是合法的
参考文献
- 具体数学·第2版 Ronald L.Graham、Oren Patashnik、Donald E.Knuth著
