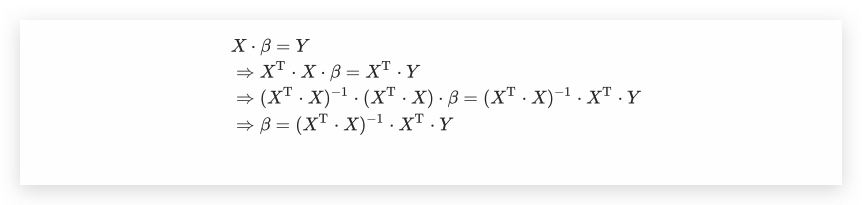最小二乘法作为一种常见的数学优化方法,其核心思想是通过对残差平方和的最小化来进行估计。这里我们将对线性条件下的最小二乘做相关说明与介绍,即 Ordinary Least Square(OLS) 普通最小二乘

线性回归
我们通过一个线性回归的例子来引入介绍OLS。这里有一组数据样本:(1,1)、(2,5)、(3,6),我们假设数据样本x、y之间呈线性关系,即我们期望采用一元线性回归模型( y=ax+b )来确定X、Y之间的具体函数关系。现在我们来将样本数据带入上述模型
我们的目的是期望通过确定参数a、b,进而确定x、y之间的函数关系。但是问题显然没有这么简单,由于多了一个样本数据致使方程组变为超定的,我们显然是无法直接求解该方程组的。那么现在我们换个思路,既然我们无法找出一条直线来满足所有给定的数据样本点,那么我们能不能找到一条直线,使得其与各个样本点之间的残差和最小?答案是肯定的,虽然这条直线不能保证经过全部的样本点,但一般可以很好地描述出x、y之间的关系。由于残差的正负问题需要添加绝对值,然而在实际计算中绝对值不好处理,故干脆直接对残差进行平方来保证非负性。其实这就是最小二乘的思想——通过对残差平方和的最小化来进行估计
则当S最小时,参数a、b即为我们所求的值,即
根据样本数据有
根据极值理论我们知道,当S取极值时,S对a和b的偏导均为0,故有
现在关于a、b的方程组是一个适定方程组,这样我们就可以直接解出参数a、b了
矩阵形式
通过上面一元线性回归的例子,我们基本了解了OLS的核心思想以及具体的计算方法。这里,我们将会给出OLS在矩阵形式下的一般通解。首先同样以上面的一元线性回归为例来进行介绍,只不过这里我们将样本数据由原来的3个变为n个,则有如下的线性方程组
我们将其改写为矩阵形式
这里我们令
则上面的矩阵即转化为:
在上文线性回归的例子中,我们说到OLS是通过残差平方和进行衡量的。故在矩阵形式中,我们的目标是找到一个向量$\beta$,使得 $X \cdot \beta - Y$的欧几里得范数最小
即
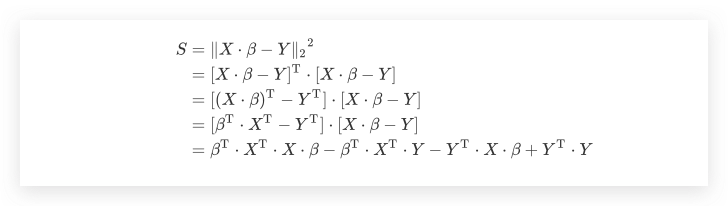
我们知道对标量转置的结果依然是其本身,由于 $\beta^\mathrm{T} \cdot X^\mathrm{T} \cdot Y$ 是一个标量,有
故
同样地,我们对 $\beta$ 求偏导

再做进一步简化之前,先介绍两个常用的矩阵公式
则上式子可进一步化简为

令其为0,如果 $(X^\mathrm{T} \cdot X)^{-1}$ 存在,则参数 $\beta$ 在OLS下的通解如下
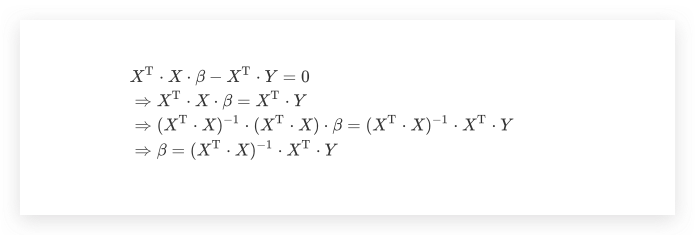
在OLS的通解形式中,$X,\beta,Y$的大小要求分别是n*m、m*1、n*1,显然此处我们的m为2
其实从OLS的矩阵通解中,我们也可以看出另外一种更为简便通解求法,直接通过左乘转置矩阵进行求解即可