xyZGHio

樱花同载酒，终似少年游

0%

浅谈Trie字典树

发表于 更新于 阅读数： 评论数：
本文字数： 6.1k 阅读时长 ≈ 12 分钟

Trie字典树，又被称为前缀树，一种可以高效进行大量字符串的保存、统计、排序等的数据结构

abstract.png

基本原理

对于字典树而言，顾名思义其首先是一棵树。然后将每个字符串拆分为若干个字符依次存储到树的各节点中。其有三个特殊的性质：

  1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符
  2. 从根节点到某一节点，将路径上经过的字符连接起来，就构成了一个字符串
  3. 每个节点的所有子节点包含的字符都不相同

假设存在hi、dog、da三个字符串，这里通过Trie树进行保存存储，则最终如下所示。可以看到Trie树的核心在于利用字符串的公共前缀减少查询时间

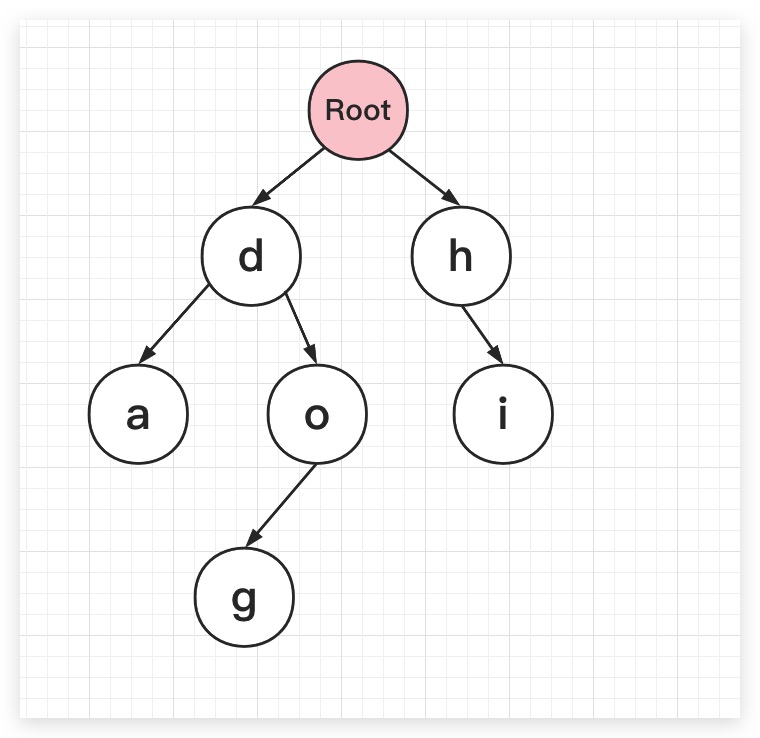
figure 1.jpeg

而在字典树的实现过程中，常见的功能包括向Trie树中插入一个字符串、判断Trie树中是否存在某字符串、判断Trie树中是否存在指定字符串前缀等，与此同时还可以提供统计、排序等高级功能

实践

实现Trie字典树

学习过程中要善于理论联系实际。故在介绍完Trie树的基本原理后，我们来实现一个Trie树。这里以LeetCode的第208题——实现Trie(前缀树)为例

请你实现 Trie 类：

  • Trie(): 初始化前缀树对象
  • void insert(String word): 向前缀树中插入字符串word
  • boolean search(String word): 如果字符串word在前缀树中，返回true（即在检索之前已经插入）；否则返回false
  • boolean startsWith(String prefix): 如果之前已经插入的字符串word的前缀之一为prefix，返回true；否则返回 false
    Note: word 和 prefix 仅由小写英文字母组成

可以看到对于本题而言，由于仅存在26个小写英文字母。故对于子节点可以通过数组进行保存，其中0～25索引 对应于 a～z 字符。同时在节点增加一个标识endFlag，用于指示当前字符是否为字符串的最后一个字符。这样查询指定字符串时，如果其最后一个字符对应节点的endFlag为true，则表示该字符串查询成功。而对于查询字符串前缀而言，只要我们能够在Trie树中查询到相应的节点存在，即可判定为查询成功。Java实现如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
/**
 * Trie字典树
 */
public class Trie {
    /**
     * 字典树的根节点
     */
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    /**
     * 字典树中插入字符串 word
     * @param word
     */
    public void insert(String word) {
        TrieNode current = root;
        char[] chars = word.toCharArray();
        for (int i=0; i<chars.length; i++) {
            char ch = chars[i];
            int index = calcIndex(ch);
            TrieNode[] childs = current.getChilds();
            if( childs[index]==null ) {
                childs[index] = new TrieNode();
            }
            current = childs[index];
        }
        current.setEndFlag( true );
    }

    /**
     * 判断字符串是否存在于字典树
     * @param word
     * @return
     */
    public boolean search(String word) {
        TrieNode current = root;
        char[] chars = word.toCharArray();
        for(int i=0; i<chars.length; i++) {
            char ch = chars[i];
            int index = calcIndex(ch);
            TrieNode[] childs = current.getChilds();
            if( childs[index]==null ) {
                return false;
            }
            current = childs[index];
        }

        return current.isEndFlag();
    }

    /**
     * 判断前缀是否存在于字典树中
     * @param prefix
     * @return
     */
    public boolean startsWith(String prefix) {
        TrieNode current = root;
        char[] chars = prefix.toCharArray();
        for(int i=0; i<chars.length; i++) {
            char ch = chars[i];
            int index = calcIndex(ch);
            TrieNode[] childs = current.getChilds();
            if( childs[index] == null ) {
                return false;
            }
            current = childs[index];
        }

        return true;
    }

    /**
     * 根据字符计算索引
     * 0～25索引 对应于 a～z 字符
     * @param ch
     * @return
     */
    private static int calcIndex(char ch) {
        return ch - 'a';
    }

    /**
     * Trie字典树节点
     */
    public static class TrieNode {
        /**
         * 子节点数组, 0～25索引 对应于 a～z 字符
         */
        private TrieNode[] childs;

        /**
         * 当前字符是否为字符串的最后一个字符
         */
        private boolean endFlag;

        public TrieNode() {
            childs = new TrieNode[26];
            endFlag = false;
        }

        public TrieNode[] getChilds() {
            return childs;
        }

        public boolean isEndFlag() {
            return endFlag;
        }

        public void setEndFlag(boolean endFlag) {
            this.endFlag = endFlag;
        }
    }
}

前K个高频单词

学习过程中要善于理论联系实际。这里以LeetCode的第692题——前K个高频单词为例

给定一个单词列表words和一个整数k，返回前k个出现次数最多的单词。返回的答案应该按单词出现频率由高到低排序;如果不同的单词有相同出现频率，按字典顺序排序

示例 1：
输入: words = [“i”, “love”, “leetcode”, “i”, “love”, “coding”], k = 2
输出: [“i”, “love”]
解析: “i” 和 “love” 为出现次数最多的两个单词，均为2次。注意，按字母顺序 “i” 在 “love” 之前

示例 2：
输入: [“the”, “day”, “is”, “sunny”, “the”, “the”, “the”, “sunny”, “is”, “is”], k = 4
输出: [“the”, “is”, “sunny”, “day”]
解析: “the”, “is”, “sunny” 和 “day” 是出现次数最多的四个单词，出现次数依次为 4, 3, 2 和 1 次

注意：

  • 1 <= words.length <= 500
  • 1 <= words[i] <= 10
  • words[i] 由小写英文字母组成
  • k 的取值范围是 [1, 不同 words[i] 的数量]

本题关键在于统计字符串的数量、获取Top K个字符串。前者可以先将字符串保存到字典树中，同时为了方便统计，我们对于树的节点增加完整字符串、计数值的字段。后者可以对字典树进行DFS深度优先遍历，并结合最小堆获取Top K个字符串。最后将最小堆中的元素进行输出即可。Java实现如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
public class Solution {
    /**
     * 获取字符串数组中Top K字符串列表
     * @param words 字符串数组
     * @param k 
     * @return
     */    
    public List<String> topKFrequent(String[] words, int k) {
        // 1. 遍历字符串存储到字典树中
        Trie trie = new Trie();
        for(String word : words) {
            trie.insert(word);
        }

        // 2. 通过最小堆、DFS获取Top K个字符串
        PriorityQueue<Trie.TrieNode> minHeap = new PriorityQueue<>();
        dfs(minHeap, k, trie.getRoot());

        // 3. 将最小堆的元素按降序输出
        LinkedList<String> res = new LinkedList<>();
        while( !minHeap.isEmpty() ) {
            Trie.TrieNode min = minHeap.poll();
            res.addFirst( min.getStr() );
        }

        return res;
    }

    /**
     * DFS搜索字典树
     * @param minHeap
     * @param k
     * @param current
     */
    private void dfs(PriorityQueue<Trie.TrieNode> minHeap, int k, Trie.TrieNode current) {
        if( current==null) {
            return;
        }

        // 字典树当前节点为完整的字符串
        if( current.getStr()!=null ) {
            // 最小堆中元素的数量未达到K, 则直接加入
            if( minHeap.size() < k ) {
                minHeap.offer( current );
            } else if( current.compareTo( minHeap.peek() )>0 ) {    // 当前节点比堆中最小的元素大, 则加入
                // 将当前节点加入最小堆
                minHeap.offer( current );
                // 将堆中最小的元素移出堆, 保证堆中数量始终为K
                minHeap.poll();
            }
        }

        // DFS搜索字典树
        for(int i=0; i<26; i++) {
            Trie.TrieNode[] childs = current.getChilds();
            dfs(minHeap, k, childs[i]);
        }
    }
}

/**
 * Trie字典树
 */
class Trie {
    /**
     * 字典树的根节点
     */
    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }

    public TrieNode getRoot() {
        return root;
    }

    /**
     * 字典树中插入字符串 word
     * @param word
     */
    public void insert(String word) {
        TrieNode current = root;
        char[] chars = word.toCharArray();
        for (int i=0; i<chars.length; i++) {
            char ch = chars[i];
            int index = calcIndex(ch);
            TrieNode[] childs = current.childs;
            if( childs[index]==null ) {
                childs[index] = new TrieNode();
            }
            current = childs[index];
        }

        // 保存完整字符串信息
        current.str = word;
        // 计数值+1
        current.count += 1;
    }

    /**
     * 根据字符计算索引
     * 0～25索引 对应于 a～z 字符
     * @param ch
     * @return
     */
    private static int calcIndex(char ch) {
        return ch - 'a';
    }

    /**
     * Trie字典树节点
     */
    public static class TrieNode implements Comparable<TrieNode> {
        /**
         * 子节点数组, 0～25索引 对应于 a～z 字符
         */
        private TrieNode[] childs;

        /**
         * 字符串
         */
        private String str;

        /**
         * 计数值
         */
        private int count;

        public TrieNode() {
            childs = new TrieNode[26];
            str = null;
            count = 0;
        }

        public TrieNode[] getChilds() {
            return childs;
        }

        public String getStr() {
            return str;
        }

        public int getCount() {
            return count;
        }

        @Override
        public int compareTo(TrieNode o) {
            // 排序规则: 先比较字符串的频率
            int res = this.count - o.count;
            if( res!=0 ) {
                return res;
            }

            // 排序规则: 频率相同, 按字典序排序
            res = o.str.compareTo(this.str);
            return res;
        }
    }
}
推荐文章
请我喝杯咖啡捏～
  • 本文作者： Aaron Zhu
  • 本文链接： https://xyzghio.xyz/Trie/
  • 版权声明： 本博客所有文章除特别声明外，均采用 BY-NC-ND 许可协议。转载请注明出处！

欢迎关注我的微信公众号：青灯抽丝