平面三点共线判定: 三阶行列式面积法

平面三点共线判定问题，常见的方法就是通过计算任意两点的斜率看是否相等来判定。但是由于斜率可能不存在、可能为零等特殊情况，处理起来略显繁琐。其实，我们可以通过利用三角形的面积公式(三阶行列式)计算三点构成三角形面积是否为零，即可优雅简洁地实现平面三点是否共线的判定

三角形面积公式

二阶行列式

给定平面三点 $A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)$ ，其所围成的三角形面积 $S_{\triangle}$ 可通过 $(1)$ 式计算：

$$S_{\triangle} = \frac{1}{2} * \left| \begin{vmatrix} x_2-x_1 & y_2-y_1 \\ x_3-x_1 & y_3-y_1 \\ \end{vmatrix} \right| \tag {1}$$

Note: 因行列式值可能为负，所以需要取绝对值

三阶行列式

给定平面三点 $A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)$ ，其所围成的三角形面积 $S_{\triangle}$ 可通过 $(2)$ 式计算：

$$S_{\triangle} = \frac{1}{2} * \left| \begin{vmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{vmatrix} \right| \tag {2}$$

Note: 因行列式值可能为负，所以需要取绝对值

沙路法则(Sarrus’ rule)

沙路法则(Sarrus’ rule)，又称对角线法则，是线性代数中二阶、三阶行列式的计算方法。其将主对角线上元素的乘积相加、次对角线上元素的乘积相减

二阶行列式

将主对角线上的元素a、d 相乘，乘积符号为正；将次对角线上的元素b、c相乘，乘积符合为负

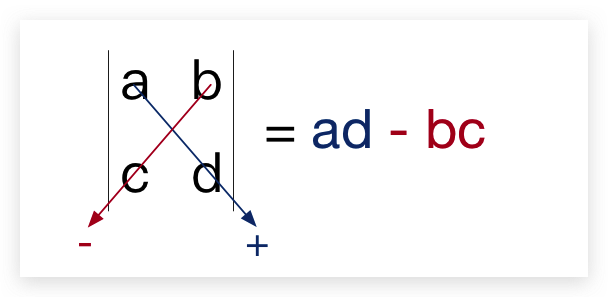
三阶行列式

三阶行列式计算时，首先需要将行列式的第1、2列复制到行列式的右侧构成第4、5列，如下图所示。再分别画出3条主对角线和3条次对角线，将各对角线上的元素相乘，然后按对角线类型主、次分别给对角线的乘积符号为正、负

平面三点共线判定

以三角形面积公式三阶行列式为例。结合沙路法则，$(2)$ 式可化为：

$$S_{\triangle} = \frac{1}{2} * \left| x_1*y_2 + x_2*y_3 + x_3*y_1 - x_1*y_3 - x_2*y_1 - x_3*y_2 \right| \tag{3}$$

当 $S_{\triangle}$ 等于0时，即所给定平面上的三点共线。由于计算机中浮点数的精度问题，不能直接判断 $S_{\triangle}$ 与 0 是否相等。而应计算 $S_{\triangle}$ 与 0 的差值，当满足指定精度 $\varepsilon_0$ 时即可认为三点共线

$$\left| S_{\triangle} - 0 \right| = \left| S_{\triangle}\right| \leq \varepsilon_0 \tag{4}$$