图,一种可以表示对象复杂连接关系的数据结构。其较可以其他数据结构而言,可以很方便描述地图、电路、网络等拓扑结构。本文将介绍图的描述方法和基本的图搜索算法——BFS 广度优先搜索

图
定义
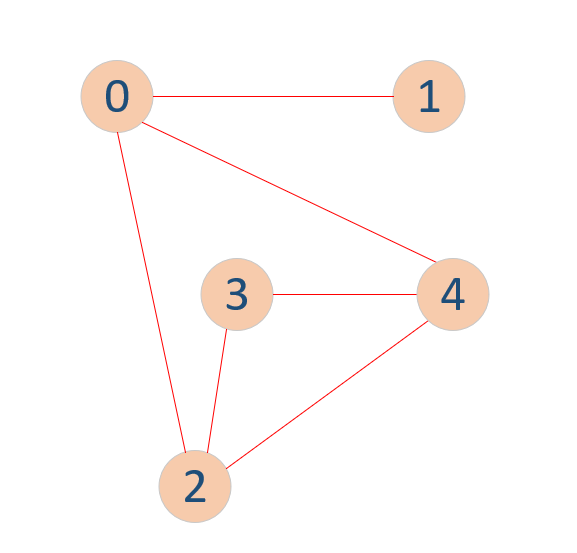
图(Graph),是由一组顶点(Vertex)和一组能够将两个顶点相连的边(Edge)所组成。具体地,根据边是否有方向,可划分为有向图、无向图;根据边是否有权重值,可划分为加权图、无加权图。如下图所示,其是一个顶点数V=5、边数E=6的无向无加权图G1(V,E)
[Note]:
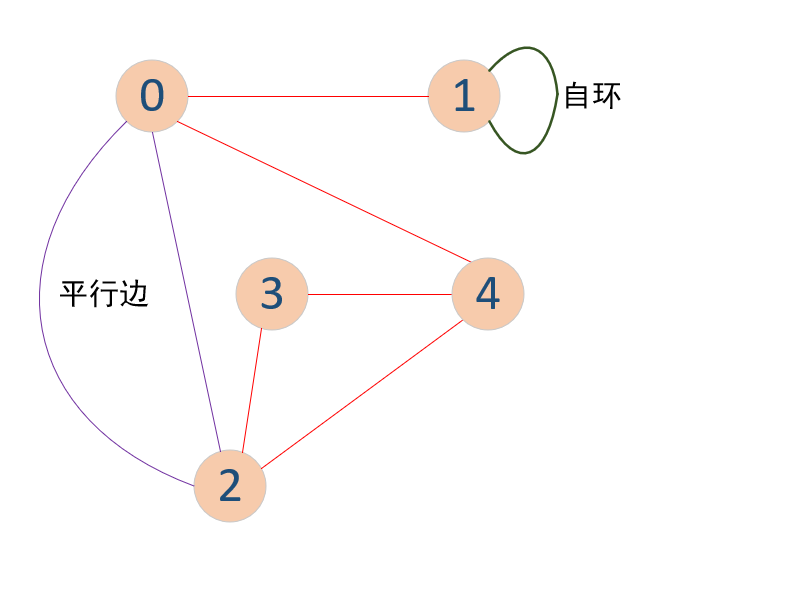
- 平行边:连接同一对顶点的两条边
- 自环:一条顶点与自身连接的边
描述
现已无向无加权图G1(V,E)为例,介绍图的表示方法
1. 邻接矩阵
邻接矩阵Adjacency Matrix,是一个 VxV 矩阵,当元素 a(v,w) 值为1时,即表示顶点v到顶点w之间有一点边。易知,无向图的邻接矩阵是一个对称矩阵;对于加权图而言,邻接矩阵中表示某条边存在的元素 a(v,w) 可设为加权值。无向无加权图G1使用邻接矩阵描述如下:
缺点:
- 当一个图很大(顶点数很多)而边数较少,此时若用邻接矩阵表示时,其矩阵是一个稀疏矩阵,且矩阵大小为VxV,这将大大浪费存储空间
- 表示无向图时,由于是对称矩阵,存在冗余,浪费存储空间
- 无法表示平行边
2.关联矩阵
关联矩阵 Incidence Matrix,是一个 VxE 矩阵,行表示顶点,列表示边。对于一个无向图而言,当某列中有2个元素的值均为1,即表示该边所连接的两个顶点。即,元素 a(v,w)、a(v,k) 值均为1时表示第v条边的两个顶点分别是w和k;对于一个有向图而言,元素 a(v,w)、a(v,k) 值分别为1、-1时,表示第v条边的起点、终点分别是w、k;当某列中,有一个元素的值为2,即可表示该顶点有一个自环;对于一个加权图而言,可以在关联矩阵下方再增加一行,用于表示各边的加权值。无向无加权图G1使用关联矩阵描述如下:
缺点:
3.邻接表
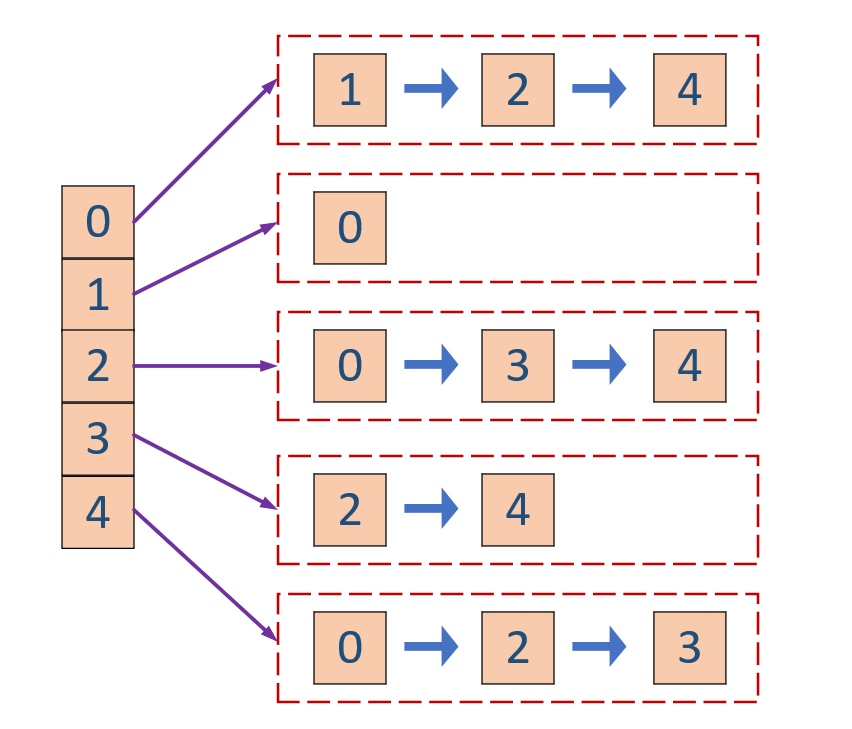
邻接表Adjacency List 是一个以顶点为索引的哈希表,然后该哈希表与每个顶点的邻接点列表相关联。无向无加权图G1使用邻接表描述如下:
BFS 算法
基本原理
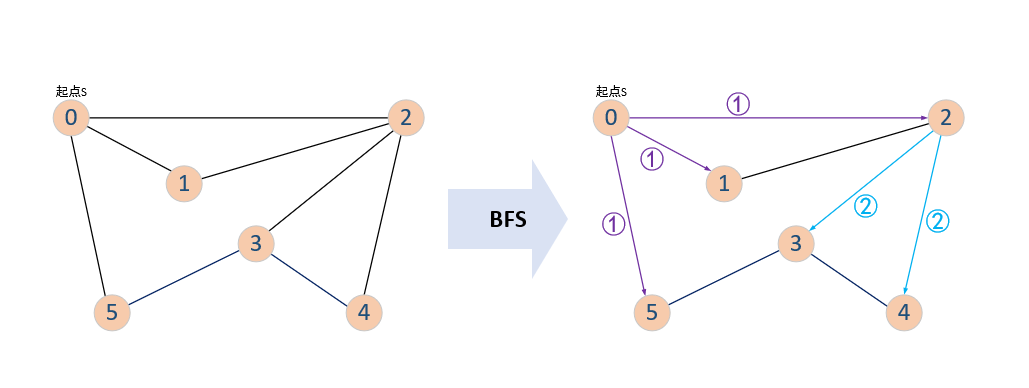
对于图而言,广度优先搜索(BFS) 和 深度优先搜索(DFS) 是两种最基础的图搜索算法,这里介绍前者——BFS。该算法主要用于解决在一个无加权图下找到从起点S至指定点W的最短路径。该算法搜索路径首先从起点S开始,查找距离起点S一条边的顶点集合中是否存在顶点W;若没有则在所有距离起点S两条边的顶点集合中继续查找,直到找到顶点W。BFS算法的搜索图解过程,如下图所示,其过程类似于走迷宫,当走到分岔处,其会自动分裂成多个人,同时向多个分岔去前进搜索;而当多个分岔合并到一处时,亦会变为一个人继续前进搜索
算法流程
为保证先搜索相同距离长度的路径,该算法使用队列的FIFO特性来保存已经遇到但还未被搜索的分岔路径
- 将起点加入队列,并将该顶点状态标记为已搜索;重复Step 2 - 4,直到队列为空
- 从队列中取出一个顶点V
- 获取顶点V所有的未被搜索过的邻接点列表 toSearchList
- 对邻接点列表 toSearchList 中所有顶点执行:加入队列、状态标记为已搜索、记录访问该顶点路径的前驱顶点
Java Demo
现已上文图解的无向图为例,通过Java实现BFS算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
|
public class BFS {
public static void BFSDemo() {
Undigraph undigraph = getUndigraph();
Integer vertexNum = undigraph.getVertexNum();
Integer start = 0;
int[] previousVertex = new int[vertexNum];
Boolean status = BFS(undigraph, start, previousVertex);
if( status ) {
visualPath(start, previousVertex);
}
}
private static Boolean BFS( Undigraph undigraph, Integer start, int[] previousVertex) {
Integer vertexNum = undigraph.getVertexNum();
Deque<Integer> deque = new LinkedList<>();
int[] markArray = new int[vertexNum];
deque.offer( start );
markArray[start] = 1;
while( !deque.isEmpty() ) {
Integer currentVertex = deque.poll();
if( !undigraph.getAdjacencyList().containsKey(currentVertex) ) {
return false;
}
List<Integer> adjacencyList = undigraph.getAdjacencyList().get(currentVertex);
for( Integer nextVertex : adjacencyList) {
if( markArray[nextVertex] != 1 ) {
markArray[nextVertex] = 1;
deque.offer( nextVertex );
previousVertex[nextVertex] = currentVertex;
}
}
}
return true;
}
private static void visualPath(Integer start, int[] resultPath) {
for( int i=0; i<resultPath.length; i++ ) {
List<String> path = new LinkedList<String>();
Integer vertex = i;
while (vertex != start) {
path.add( vertex.toString() );
vertex = resultPath[vertex];
}
path.add(vertex.toString());
Collections.reverse(path);
String pathStr = path.stream().collect( Collectors.joining("->") );
System.out.println(pathStr);
}
}
private static Undigraph getUndigraph() {
Map<Integer, List<Integer>> adjacencyList = new HashMap<>();
adjacencyList.put(0, Arrays.asList(1, 2, 5) );
adjacencyList.put(1, Arrays.asList(0, 2) );
adjacencyList.put(2, Arrays.asList(0, 1, 3, 4) );
adjacencyList.put(3, Arrays.asList(2, 4, 5) );
adjacencyList.put(4, Arrays.asList(2, 3) );
adjacencyList.put(5, Arrays.asList(0, 3) );
Undigraph undigraph = new Undigraph();
undigraph.setAdjacencyList( adjacencyList );
undigraph.setVertexNum( adjacencyList.size() );
return undigraph;
}
}
@Data
class Undigraph {
private Map<Integer, List<Integer>> adjacencyList;
private Integer vertexNum;
}
|
算法结果:

应用
参考文献
- 算法(第4版) Robert Sedgewick、Kevin Wayne 著






