Couting Sort 计数排序虽然快,但其只能对整数进行排序有一点的局限性。而 Bucket Sort 桶排序则没有这个限制。这里我们就来详细介绍该算法,其一般在排序元素的值基本处于均匀分布的场景下应用
算法思想
在Bucket Sort 桶排序中,我们首先需要设置k个桶用于存储排序元素。先根据映射函数将各排序元素依次放置到合适的桶中,最后对各个桶内的元素进行桶内排序;由于各桶之间是有序的,故遍历各个桶将桶内的有序序列直接拼接起来即可
Note:
对桶内元素进行排序时,排序算法不限,但桶内排序算法的稳定性将会直接决定Bucket Sort桶排序的稳定性
设计与实现
桶数、映射函数
在桶排序中,最理想的情况就是每个桶中只被分配一个元素,这样就可以直接避免桶内排序这一步;最坏的情况就是所有元素全部分配到一个桶中,此时桶排序就会完全退化为一个桶内排序,所以排序元素能否均匀地分配到各个桶中将会直接影响桶排序的性能,故一般当排序元素的值基本为均匀分布时才会应用该算法进行排序。对于桶排序算法而言,最重要的就是桶数与映射函数的设计,其同样会影响桶排序的性能,这里我们来介绍一种均匀分配的设计方案
对于N个元素而言,令其取值范围为 gap(即 elementMaxValue-elementMinValue),易知其可构成 N-1 个区间长度 length 为 gap/(N-1) 的左闭右开区间。由于是左闭右开区间,会使得最后一个区间的右端点无法取到,即排序元素中的最大值elementMaxValue无法被cover,故我们又在后面增加了一个同样长度的区间。如下图所示
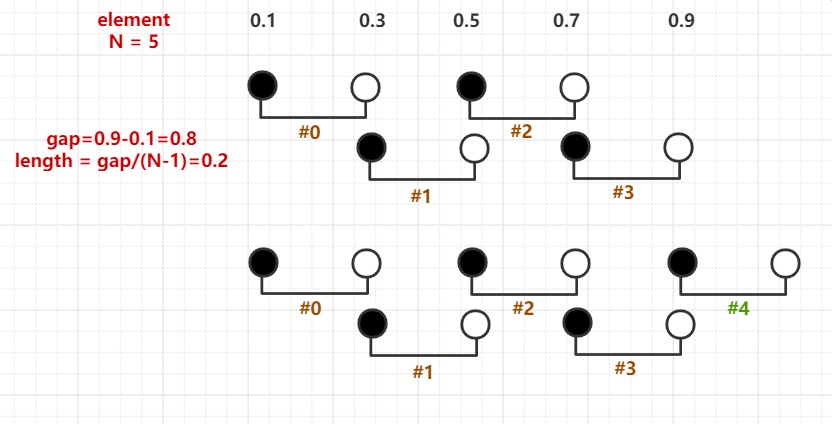
至此,我们就将排序元素划分为了N个区间(如上图所示,区间从0开始编号),而对于某个排序元素所属区间的编号 intervalNumber 可通过下式计算获得:
intervalNumber = floor( (elementValue - elementMinValue) / length )
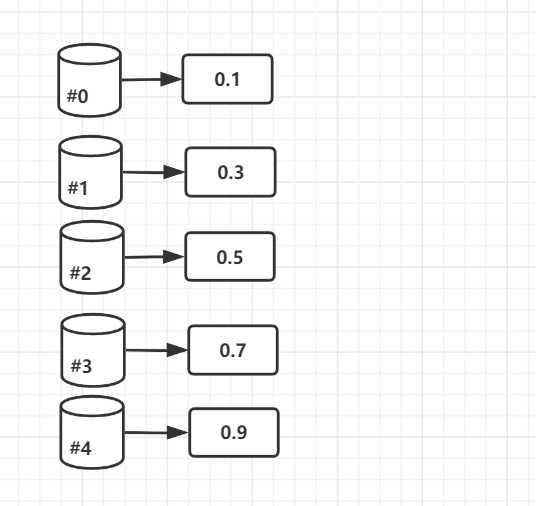
聪明的朋友可能已经看出来了,这里的区间实际上就是桶排序所需要的桶,而上式计算区间编号的公式即是我们所需的映射函数。在均匀分配的设计方案下,我们会使用N个桶,然后通过上式来计算各排序元素应该在放到哪个桶中。下图所示的结果,每个桶恰好只分配到了一个元素。实际上,一个桶可能会被分配多个元素,所以对于桶内元素一般采用链表进行存储
实现
我们通过Java来实现桶排序,使大家更好地理解该算法。这里对于桶内排序,我们使用的插入排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
|
public class BucketSort {
public static void sort() {
double[] array = getTestCase();
System.out.println("before sort: " + Arrays.toString(array) );
if( array.length>1 ) {
bucketSort(array);
}
System.out.println("after sort: " + Arrays.toString(array) );
}
private static void bucketSort(double[] array) {
int k = array.length;
ArrayList<ArrayList<Double>> buckets = new ArrayList<>(k);
for(int i=0; i<k; i++) {
buckets.add(new ArrayList<>());
}
double[] minMax = getMinMax(array);
double min = minMax[0];
double max = minMax[1];
double gap = max - min;
double bucketLength = gap / (k-1);
for(double element : array) {
int bucketIndex = (int)Math.floor( (element - min)/bucketLength );
ArrayList<Double> listInBucket = buckets.get(bucketIndex);
listInBucket.add(element);
}
for(ArrayList<Double> listInBucket : buckets) {
if( listInBucket.size()<=1 ) {
continue;
}
insertSort( listInBucket );
}
int index = 0;
for(ArrayList<Double> listInBucket : buckets) {
if( listInBucket==null ) {
continue;
}
for(Double element : listInBucket) {
array[index] = element;
index++;
}
}
}
private static double[] getMinMax(double[] array) {
double min = Double.MAX_VALUE;
double max = Double.MIN_VALUE;
for(double element: array) {
min = Double.min(element, min);
max = Double.max(element, max);
}
double[] minMax = new double[]{min,max};
return minMax;
}
private static void insertSort(ArrayList<Double> list) {
int size = list.size();
for(int i=1; i<size; i++) {
double element = list.get(i);
int j = i-1;
for(; j>=0 && list.get(j)>element; j--) {
list.set(j+1, list.get(j));
}
list.set(j+1, element);
}
}
private static double[] getTestCase() {
double[] caseArray = {-1.2, 1.1, 4.3, 6.32, 8.35, 1.2, 4.4, 6.51};
return caseArray;
}
}
|
测试结果如下:
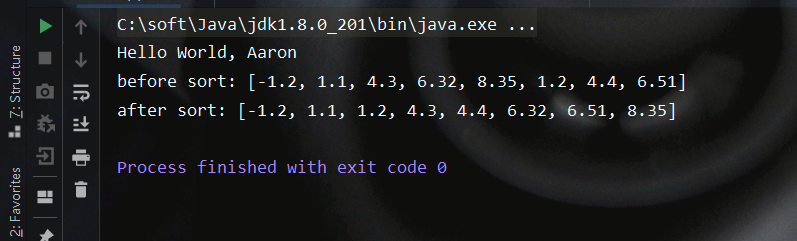
特点
空间复杂度
由于需要分配k个桶,且k个桶一共存储了N个元素,故其空间复杂度为 O(N + k)
时间复杂度
1. 最坏的情况
当N个排序元素全部被分配到一个桶中,此时桶排序算法即退化为对该桶的N个元素的全排序,这时,其时间复杂度将取决于桶内算法。如果桶内排序使用的为插入排序,则其复杂度为平方时间;如果桶内排序使用的为快速排序,则其复杂度为线性对数时间
2. 最好的情况
当每个桶中的被分配到的元素最多不超过1个时,其复杂度为线性时间
3.平均的情况
当桶内排序为平方时间复杂度的插入排序,其桶排序在平均情况下的时间复杂度为O(N+k+N*N/k)
稳定性
如上文所述,桶排序的稳定性取决于桶内排序所使用排序算法的稳定性。本文使用插入排序进行桶内排序,故其稳定;如若在桶内使用不稳定的快速排序,此时桶排序即为不稳定的
其它
- 桶排序虽然没有计数排序所要求的排序元素必须为整数的限制,但其一般也只用于排序元素基本为均匀分布的场景,否则桶排序会发生退化,致使算法效率严重下降
- 该算法的桶数、映射函数设计的好坏会极大程度地影响算法性能
- 空间复杂度较高,属于典型地用空间换时间的策略
参考文献
- 算法导论 · 第3版




