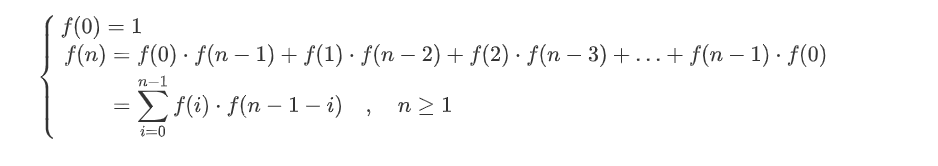斐波那契数列对于很多人来说并不陌生,但对于Catalan Number卡塔兰数可能就那么熟悉了,其实它是一个组合数学中常在计数问题出现的数列

Catalan Number 卡塔兰数
Catalan Number 卡塔兰数,是一个组合数学中常在计数问题出现的数列。其前10项依次是:1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862。初看,会觉得这个数列没有明显规律,其实不然,其公式如下:
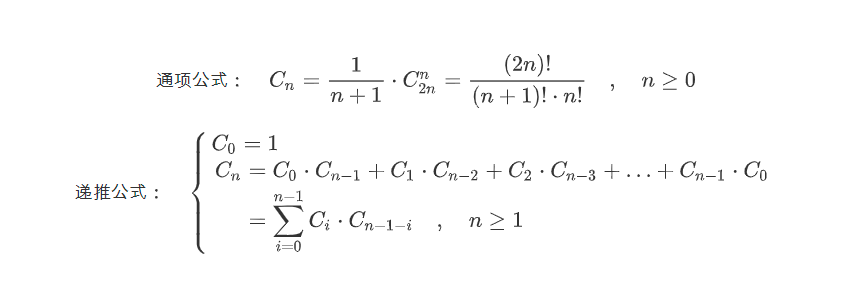
出栈顺序问题
问题描述如下:假设有N个数字依次入栈:1,2,3,…,n,试问有多少种出栈顺序?这里为表述简便,下文用+1表示一个元素入栈,用-1表示一个元素出栈
- 假设n为1时,只有一种出栈顺序:
- 1入栈,1出栈。即,+1,-1
- 假设n为2时,则有两种出栈顺序:
- 1入栈,2入栈,2出栈,1出栈。即,+1,+1,-1,-1
- 1入栈,1出栈,2入栈,2出栈。即,+1,-1,+1,-1
可是如果n为3时,该如何计算出栈顺序呢?如果采用暴力枚举显然十分麻烦。那么我们换个思路,首先来观察n为2时的一个出栈序列:+1,+1,-1,-1。可以看到对于一个合理正确的出栈序列而言,其前任意项的和均不会小于0。当然这一点也很好理解,因为出栈的前提是栈里必须要有元素;而对于 +1,-1,-1,+1 这样一个出栈序列,显然是非法的,因为其前3项的和小于0
如果我们能够找到所有错误的出栈序列,那么自然就可以知道正确合理的出栈序列有多少种了。那么问题就转换成找出n为3时全部错误的出栈序列了,显然通过暴力枚举的方法是不合适的,因为反正都是用暴力枚举,那何必多此一举?直接枚举正确的出栈序列就好了啊。这里,我们需要先对错误的出栈序列做一个映射f,根据上文我们知道,对于一个错误的出栈序列,其必然存在一个最小的k使得该出栈序列的前k项为-1。那么我们的映射f是这样,对该出栈序列的前k项取相反数,其余项保持不变,来得到一个新的序列
这里下图n为3时的一个错误出栈序列S1进行说明,其前3项的值为-1,那么通过映射f将S1的前3项进行取相反数,其余项保持不变,则可以得到序列S2
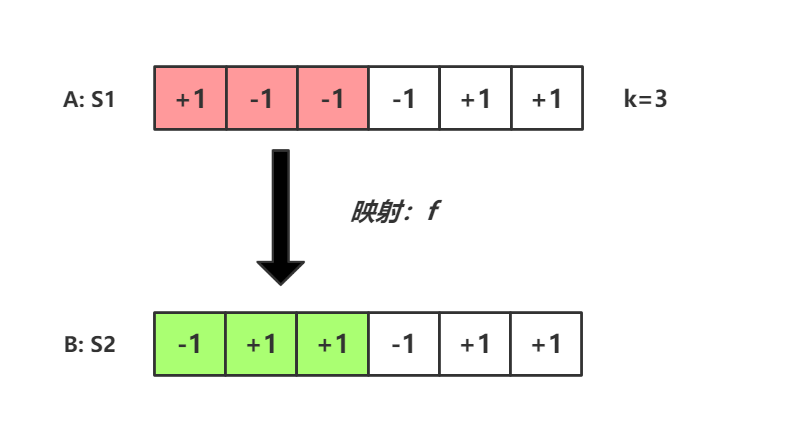
由于S1的前k项中,-1比+1多一个,那么对于将前k项取了相反数的S2序列而言,其+1项为n+1个而-1项仅有n-1个,且其前k项和必为1。具体地,对于这里n=3的情形而言,S2序列的+1项为4个,-1项为2个。这里我们将所有错误的出栈序列定义为集合A,将对集合A进行映射f后的集合定义为集合B。显然集合A与集合B的映射f是一个一对一的映射,因为,集合A的一个错误序列S1经过映射f后只会得到集合B的一个S2序列;而同时对于集合B的一个S2序列而言,其也必然存在一个最小的k使得S2序列的前k项为1,同样地,将S2序列的前k项取相反数,其余项保持不变,也只会得到集合A中的一个S1序列。这样我们只需要统计集合B中序列的数量即可知道集合A中的错误序列的数量。现在根据组合的定义我们知道,当n为3时集合B中序列的数量,也即错误出栈顺序的数目为:
而正确的出栈顺序与错误的出栈顺序数目之和为:
故,我们知道当n为3时正确出栈顺序的数目为:
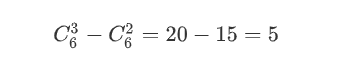
推广至n,则可知正确出栈顺序的数目如下所示,可以看到发现其是Catalan Number的通项公式
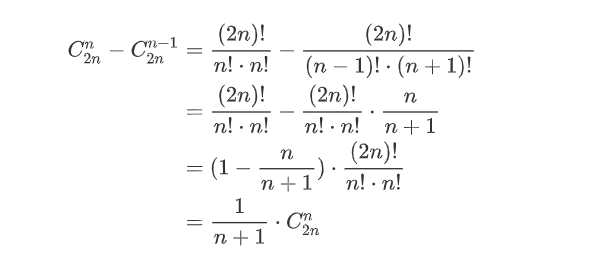
括号序列问题
问题描述:有n对()括号,试问可以组成多少种合法正确的括号序列?
其实这个问题和上面的出栈顺序问题本质上一致的,将上文的正确出栈序列的-1、+1分别用(、)代替即为正确合法的括号序列,以n为2为例说明:
- 正确的出栈序列:+1,+1,-1,-1,对应于合法的括号序列即为:(())
- 正确的出栈序列:+1,-1,+1,-1,对应于合法的括号序列即为:()()
但是这里我们提供一种新的思路来解决该问题,首先记n对()括号可以组成的正确括号序列的数量为f(n)。特别地,我们规定f(0)=1。易知:
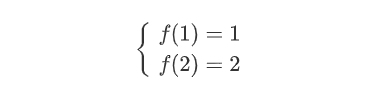
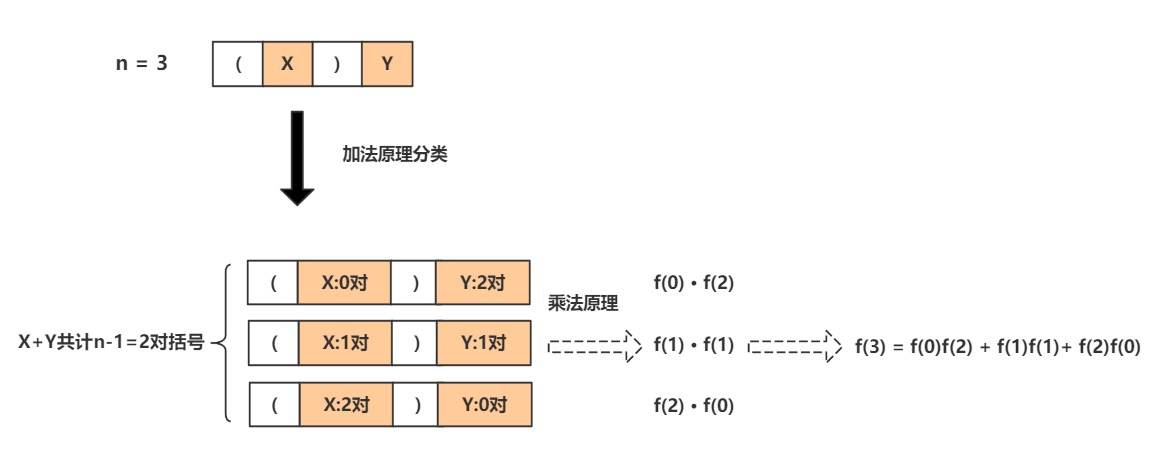
同样我们先分析n为3时的情形,如下图所示。我们先使用1对()括号,然后对剩余X、Y部分来说,一共可以使用的()括号将只有n-1对,那么我们先通过加法原理可以将X、Y部分的括号使用情况分为3类,然后对于任一分类的情形下,我们再用乘法原理来计算该分类下正确的括号序列的数量
现在我们就可以知道当n为3时,正确括号序列的数量为:
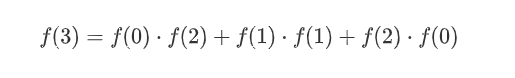
推广至n,则可知正确括号序列的数量如下所示,可以看到发现其恰好是Catalan Number的递推公式