排序算法(六): Counting Sort 计数排序

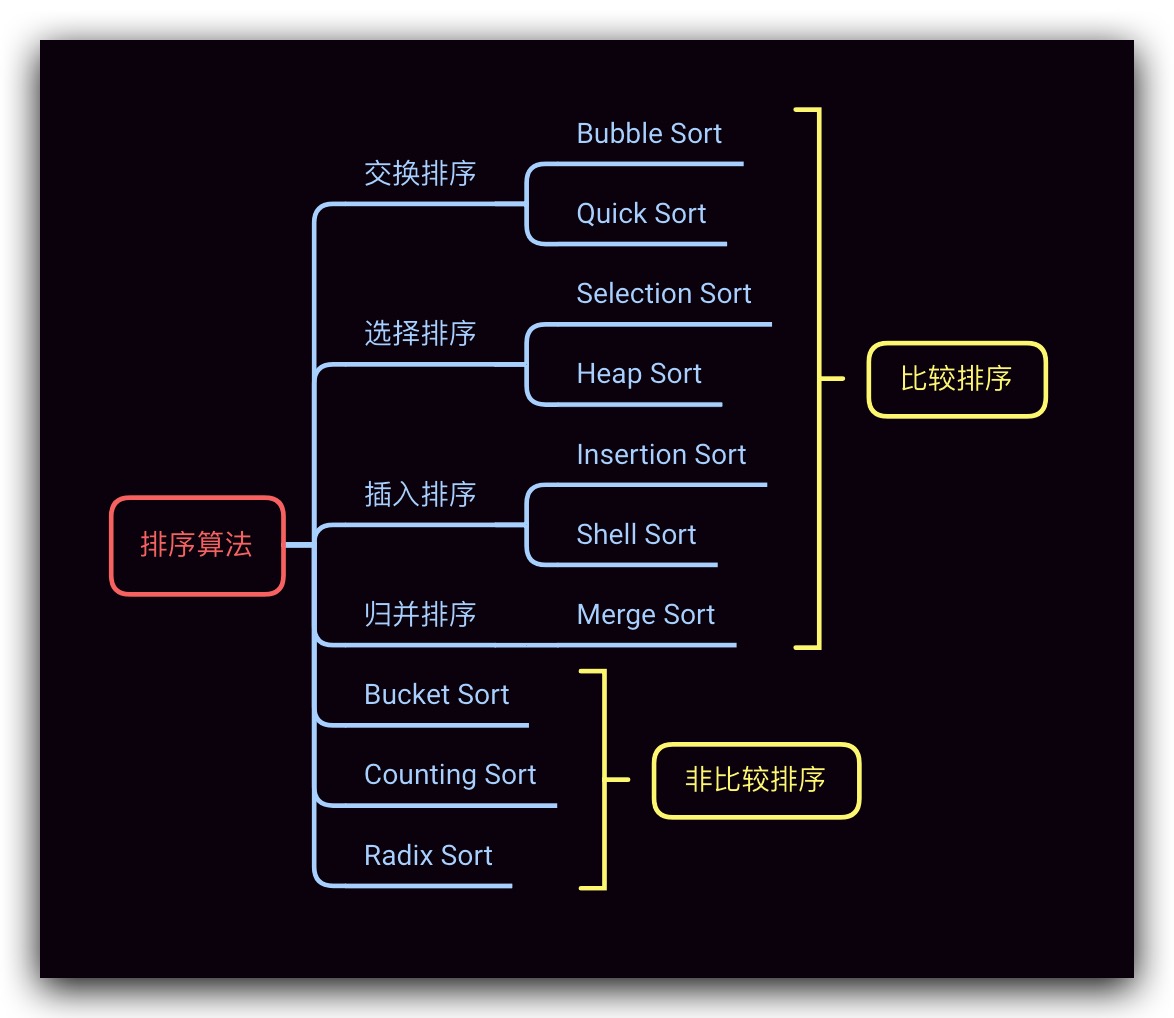
之前文章介绍的一些排序算法都是基于比较来进行排序的，故它们在平均情况下的时间复杂度最好也不过是线性对数级别。这里我们来介绍一种简单的基于非比较的排序算法——Counting Sort 计数排序，其时间复杂度可以达到线性级别

基本思想

Counting Sort 计数排序，顾名思义，就是统计待排序数组元素的出现次数。其基本思想比较简单：

1. 根据待排序元素的数值范围大小k(max-min+1)，建立一个k大小的频数统计数组counts。对于counts数组而言，其索引范围 0 ~ k-1，正好可以对应到待排序元素的取值范围min~max上
2. 统计待排序元素element的次数，并其存储到counts数组中，即counts[ elemet-min ] = countValue

3. 待计数统计完成后遍历counts数组，根据次数值来输出原待排序元素值，此时即完成排序

   这里给出计数排序在Java下的实现：

/**
 * 计数排序
 */
public class CountingSort {

    /**
     * 升序排列 (非稳定)
     */
    public static void sort1() {
        // 获取测试用例
        int[] array = getTestCase();
        int size = array.length;

        System.out.println("before sort: " + Arrays.toString(array) );

        // 求取最值
        int[] minMax = getMinMax(array);
        int min = minMax[0];
        int max = minMax[1];

        // 根据数据范围创建统计数组
        int k = max-min+1;
        int[] counts = new int[ k ];

        // 统计原数组中元素出现的次数
        for(int i=0; i<size; i++) {
            int dataInCountIndex = array[i] - min;    // 计算原数组元素在统计数组中的索引
            counts[dataInCountIndex] +=1;             // 统计该值次数
        }

        int j = 0;  // 有序的数据的插入位置
        for(int i=0; i<k; i++) {
            int originalData = i + min; // 还原 原排序数组的数据值
            while( counts[i]>0 ) {
                array[j] = originalData;
                counts[i]--;    // 该数值出现的次数减1
                j++;            // 更新有序数据的插入位置
            }
        }

        System.out.println("after sort: " + Arrays.toString(array) );
    }  

    /**
     * 求指定数组的最值
     * @param array
     * @return [0]: 最小值; [1]: 最大值;
     */
    private static int[] getMinMax(int[] array) {
        int min = array[0];
        int max = array[0];
        for(int i=1; i<array.length; i++) {
            if( array[i]>max ) {
                max = array[i];
            }
            if( array[i]<min ) {
                min = array[i];
            }
        }
        int[] minMax = new int[]{min,max};
        return minMax;
    }

    /**
     * 获取测试用例
     */
    private static int[] getTestCase() {
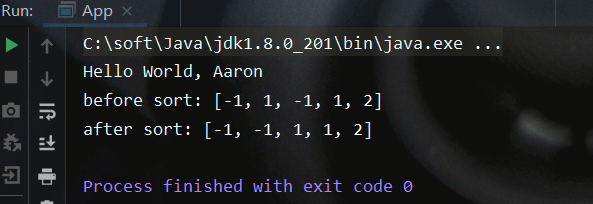
        int[] caseArray = {-1,1,-1,1,2};
        return caseArray;
    }
}

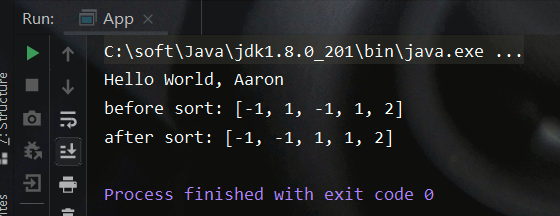
测试结果如下：

稳定的计数排序

基本原理

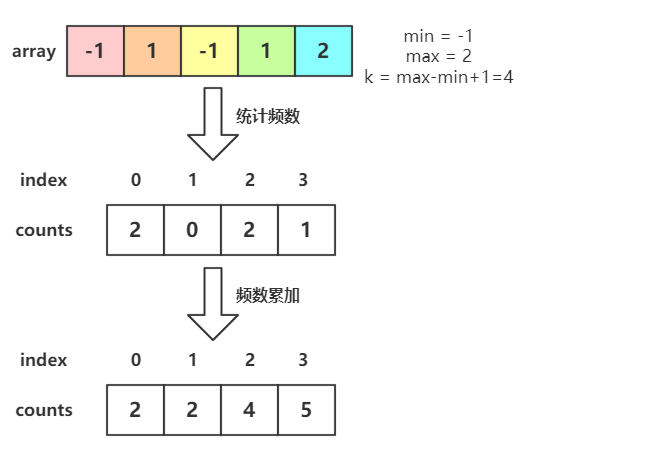
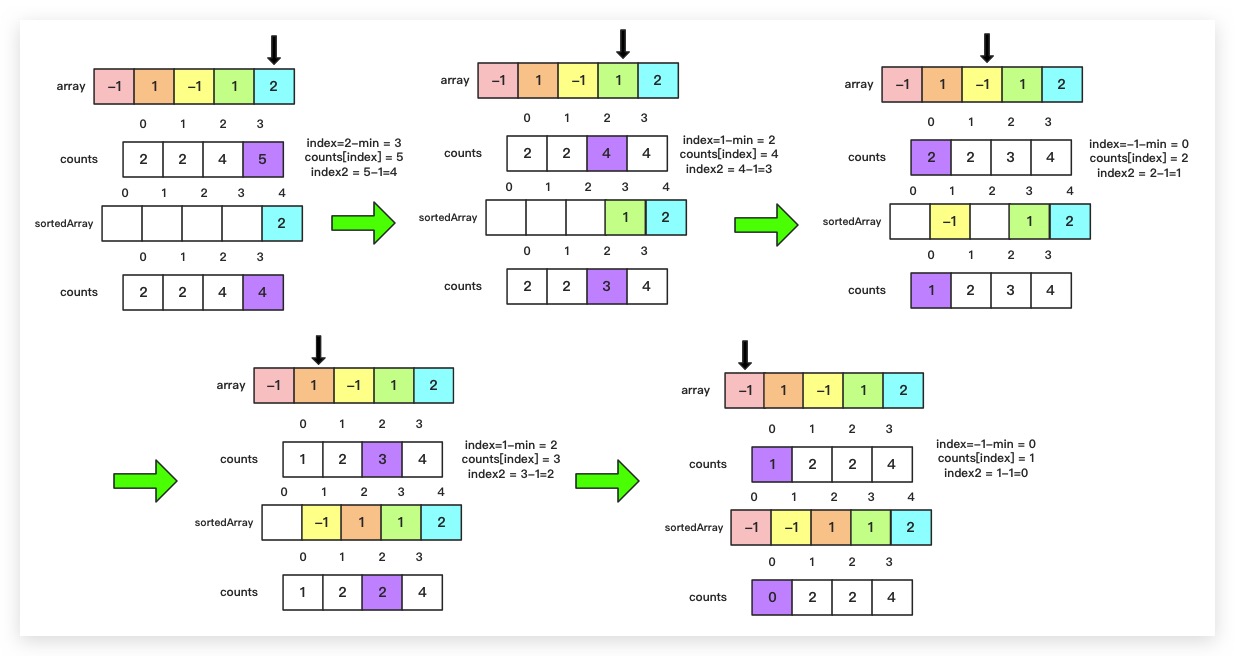
上面的计数排序算法是非稳定的，而一般我们所说的计数排序都是稳定的。那么如何保证计数排序的稳定性呢？其实很简单，只需在统计完待排序元素的频数后，对counts作累加计算（counts[i] = counts[i-1] + counts[i]），即计算统计数组中指定索引位置上的元素在排序后的位置；然后倒序遍历原数组，根据counts数组中的排序位置来将待排序元素放入合适的位置，同时将counts数组相应的值减1，以使下一个重复的排序元素可以放在前一位的位置上，以保证稳定性

算法图解

下图即是通过稳定的计数排序对 -1,1,-1,1,2 序列进行升序排列的图解过程

1. 建立counts数组

2. 倒序遍历原待排序数组，按升序排列

Java实现

这里给出计数排序在Java下的实现：

/**
 * 计数排序
 */
public class CountingSort {
    ...
    /**
     * 升序排列 (稳定)
     */
    public static void sort2() {
        // 获取测试用例
        int[] array = getTestCase();
        int size = array.length;

        System.out.println("before sort: " + Arrays.toString(array) );

        // 求取最值
        int[] minMax = getMinMax(array);
        int min = minMax[0];
        int max = minMax[1];

        // 根据数据范围创建统计数组
        int k = max-min+1;
        int[] counts = new int[ k ];

        // 统计原数组中元素出现的次数
        for(int i=0; i<size; i++) {
            int dataInCountIndex = array[i] - min;    // 计算原数组元素在统计数组中的索引
            counts[dataInCountIndex] +=1;             // 统计该值次数
        }

        // 计算统计数组的累计值，即计算 统计数组中指定索引位置上的元素在排序后的位置
        // 如果该索引位置上有重复元素，则为重复元素所占的最大排序位置
        for(int i=1; i<k; i++) {
            counts[i] = counts[i-1] + counts[i];
        }

        int[] sortedArray = new int[size];  // 排序结果数组
        // 倒序遍历原数组，保证稳定性
        for(int i=size-1; i>=0; i--) {
            int dataInCountIndex = array[i] - min;  // 计算原数组元素在统计数组中的索引
            // 计算其排序后的位置, 因为数组索引从0开始计算，故应对排序位置减1
            // 例如，排在最前面的元素，排序位置为1，则其在数组中的位置索引应为0
            int sortIndex = counts[dataInCountIndex] - 1;
            sortedArray[sortIndex] = array[i]; // 将原数组元素放入排序后的位置上
            counts[dataInCountIndex]--;        // 下一个重复的元素，应排前一个位置，以保证稳定性
        }

        System.out.println("after sort: " + Arrays.toString(sortedArray) );
    }
    ...    
}

测试结果如下：

特点

复杂度、稳定性

这里以稳定的计数排序进行说明：

时间复杂度	空间复杂度	稳定性
$O(N + k)$	$O(N + k)$	稳定

缺陷

1. 计数排序只能适用待排序元素为整数的场景
2. 待排序元素的数值范围(极差)过大的情况下，计数排序会浪费大量空间，故一般不推荐使用计数排序

参考文献

1. 算法导论 · 第3版