DFS 深度优先搜索

发表于 | 更新于: | | 阅读数
字数统计: 875 | 阅读时长 ≈ 3

在上一次的文章中，我们介绍了图的一些基础知识及图的基础搜索算法之中的广度优先搜索BFS。本文我们介绍另外一种基础的图搜索算法——DFS 深度优先搜索

abstract

DFS 算法

基本思想

众所周知，BFS算法是按广度进行搜索遍历的。其对于一个顶点的分岔路径，是采用类似于轮询的思想，通过依次遍历的方式去处理；而对于DFS算法而言，故名思义，其按照图的深度进行遍历搜索的。其在一个顶点遇到分岔路径时，会选择其中一条未被访问过的路径继续前进搜索，周而复始、一条路走到黑，直到其发现已经无路可走；此时，其根据走过的路径回溯到上一个顶点；然后判断此处是否存在新的未被访问过的分岔路径可供前进搜索；如果存在，则前进搜索，否则，继续回溯，回溯到上上一个顶点。DFS算法的图解过程，如下所示：

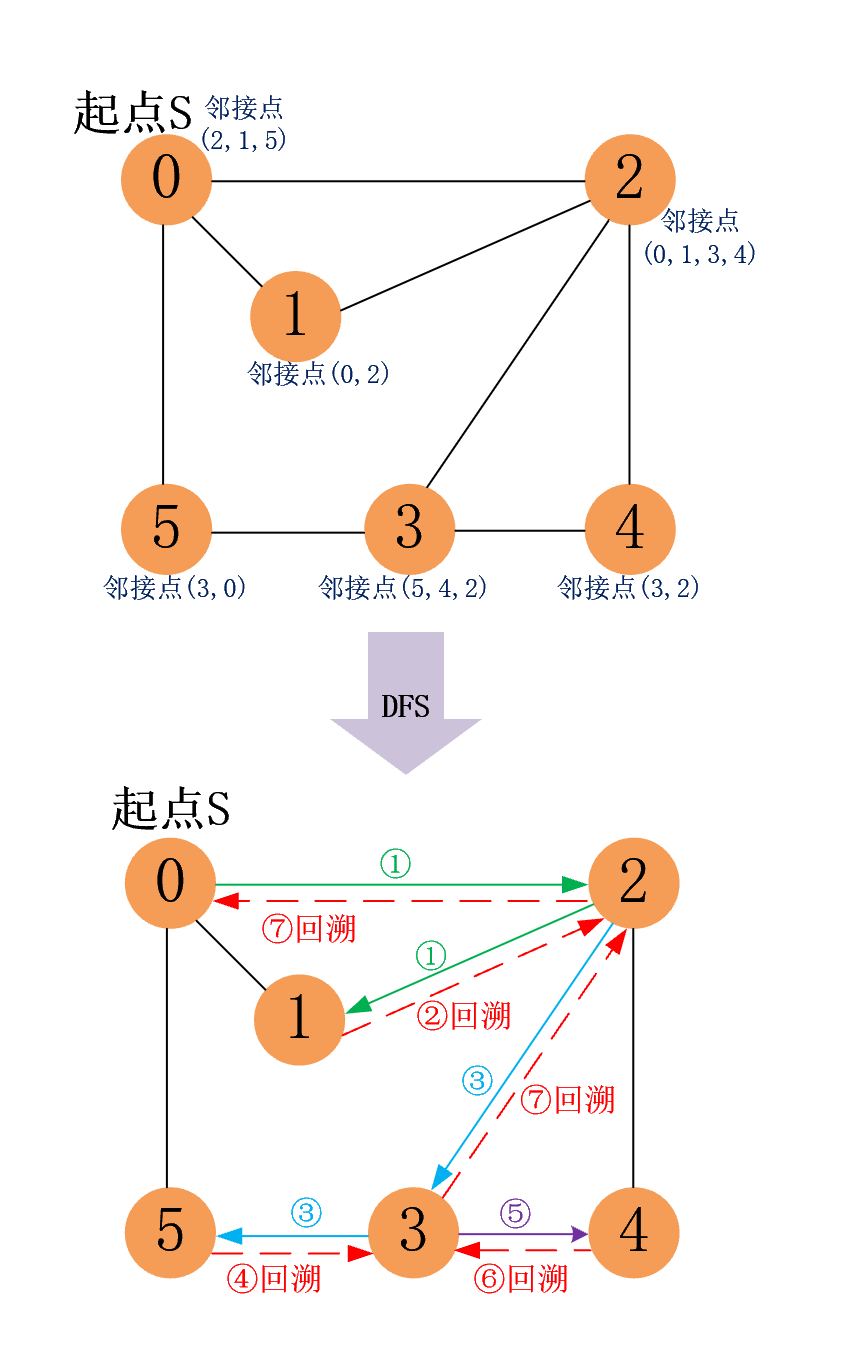
figure 1.png

算法流程

该算法通过递归即可实现按深度搜索顶点，算法流程如下：

  1. 指定搜索起点，记为顶点V
  2. 将顶点V的访问状态标记为已搜索
  3. 获取顶点V所有的未被搜索过的邻接点列表 toSearchList
  4. 遍历邻接点列表 toSearchList 依次取出元素执行：将顶点记为V、记录访问该顶点路径的前驱顶点、重复 Step 2-4

Java Demo

现已上文DFS图解的无向图为例，通过Java实现DFS算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
/**
 * DFS Algorithm Demo
 */
public class DFS {

    /**
     *  访问状态标记数组, 0: 未访问; 1: 已访问
     */
    private static int[] markArray;

    /**
     * DFS搜索结果: 从起点到该点的最短路径上的上一个位置点
     * 即 previousVertex[v] = w, 意为 start → ... → w → v
     */
    private static int[] previousVertex;

    public static void DFSDemo() {

        Undigraph undigraph = getUndigraph();           // 通过邻接表构造一个无向图
        Integer vertexNum = undigraph.getVertexNum();   // 该无向图的顶点数
        markArray = new int[vertexNum];                 // 顶点访问状态标记数组
        previousVertex = new int[vertexNum];            // DFS搜索结果


        Integer start = 0;      // 指定遍历起点

        Boolean status = DFS(undigraph, start);
        if( status ) {
            visualPath(start, previousVertex);
        }
    }

    /**
     * 深度优先遍历
     * @param undigraph 图
     * @param vertex 起点
     * @return
     */
    private static Boolean DFS( Undigraph undigraph, Integer vertex) {
        markArray[vertex] = 1;  // 标记状态为 已访问

        // 该点无邻接点
        if( !undigraph.getAdjacencyList().containsKey(vertex) ) {
            return false;
        }

        // 取出该点的邻接点列表
        List<Integer> adjacencyList = undigraph.getAdjacencyList().get(vertex);
        for( Integer adjacencyVertex : adjacencyList ) {
            // 当前点的邻接点未访问，则进行访问
            if( markArray[adjacencyVertex] != 1  ) {
                previousVertex[adjacencyVertex] = vertex; // 记录访问路径
                DFS(undigraph, adjacencyVertex);          // 通过递归按深度搜索
            }
        }
        return true;
    }

    /**
     * DFS 结果可视化
     * @param start 起点
     * @param resultPath DFS结果路径
     */
    private static void visualPath(Integer start, int[] resultPath) {
        for( int i=0; i<resultPath.length; i++ ) {
            List<String> path = new LinkedList<String>();
            Integer vertex = i;
            while (vertex != start) {
                path.add( vertex.toString() );
                vertex = resultPath[vertex];
            }
            path.add(vertex.toString());
            Collections.reverse(path);
            String pathStr = path.stream().collect( Collectors.joining("->") );
            System.out.println(pathStr);
        }
    }

    /**
     * 根据邻接表构造无向图
     * @return
     */
    private static Undigraph getUndigraph() {
        Map<Integer, List<Integer>> adjacencyList = new HashMap<>();

        adjacencyList.put(0, Arrays.asList(2, 1, 5) );
        adjacencyList.put(1, Arrays.asList(0, 2) );
        adjacencyList.put(2, Arrays.asList(0, 1, 3, 4) );
        adjacencyList.put(3, Arrays.asList(5, 4, 2) );
        adjacencyList.put(4, Arrays.asList(2, 3) );
        adjacencyList.put(5, Arrays.asList(3, 0) );

        Undigraph undigraph = new Undigraph();
        undigraph.setAdjacencyList( adjacencyList );
        undigraph.setVertexNum( adjacencyList.size() );
        return undigraph;
    }
}

算法结果：

figure 2.jpeg

参考文献

  1. 算法(第4版) Robert Sedgewick、Kevin Wayne 著
0%