Bloom Filter 布隆过滤器

哈希表（又称作散列表）这种数据结构，通过计算元素在哈希表中的存储位置，可以快速判定该元素是否存在于该哈希表中，而无需遍历哈希表中全部元素一一进行比较。看上去哈希表这种数据结构是一个很好的工具，但是当数据量非常大达到亿级别，再加上为了解决哈希冲突的负载因子的缘故，使得哈希表的内存空间开销非常巨大，甚至会出现机器内存都无法支撑的情况。这种超大规模数据的场景下，如何快速判定一个元素是否在指定元素集合中？本文将详细介绍一种概率模型的数据结构——布隆过滤器（Bloom Filter）

基本原理

在哈希表中存放的是元素本身，而 Bloom Filter 在内存中是一个足够大的位数组(Bit Array)，其最小的内存使用单位是Bit(仅这一点，内存开销就已经大大压缩了)。元素在插入Bloom Filter时，使用哈希函数(Hash Function)计算其哈希值确定其在位数组中的位置索引，然后将位数组中的指定Bit从0置1即可(如该Bit已经被置1，则无需再次置1)。当使用Bloom Filter判定指定元素是否存在其中时，同样利用该Hash Function先计算哈希值，确定其在位数组的中位置索引，然后取出该位置的值， 若该Bit为0，则说明该元素不存在于其中；若该Bit为1，则说明该元素存在于其中

现已向一个Bloom Filter分别插入元素”Hello”、”World”为例，给出其插入过程的图解

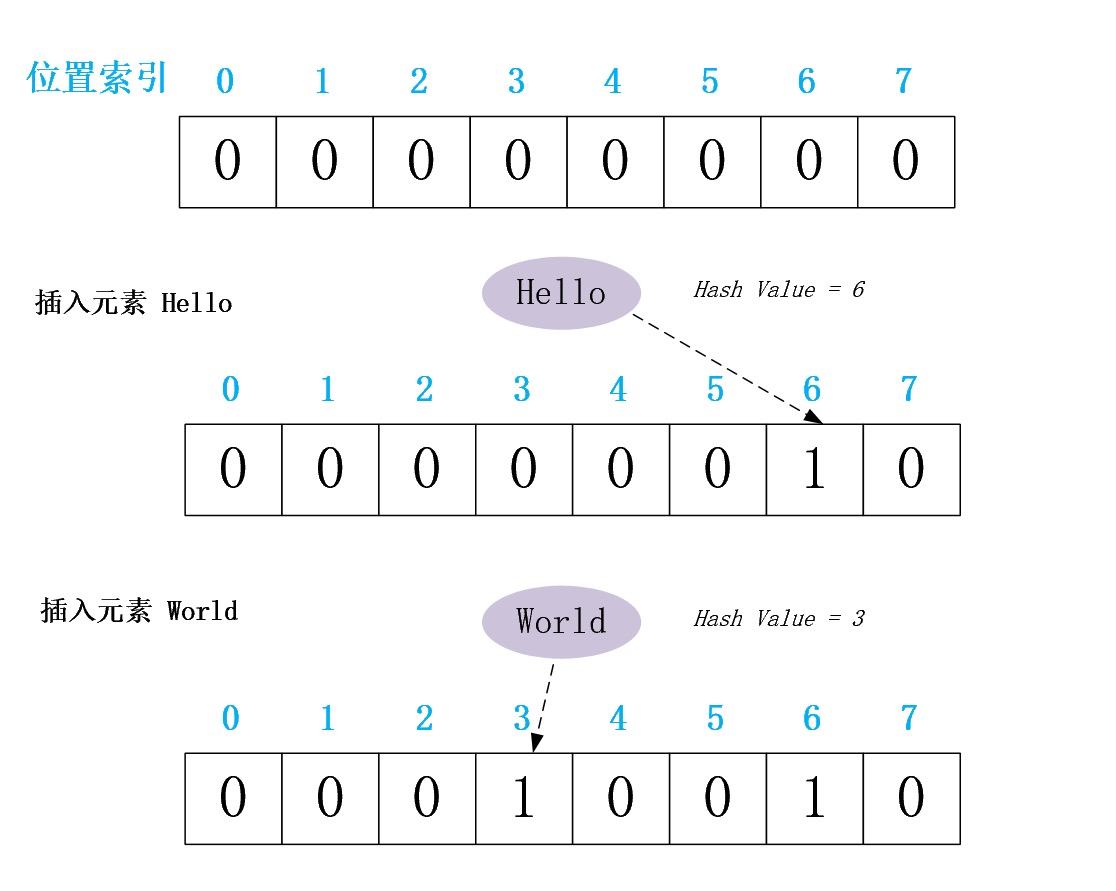
当判断元素”World”是否在该Bloom Filter中时，先利用Hash Function计算其哈希值(Hash Value = 3)，确定其在位数组的中位置索引，然后取出该位置的值(即，BitArray[3])，其值为1，即说明元素”World”存在于该Bloom Filter中；当判断元素”Tony”是否在该Bloom Filter中时，先利用Hash Function计算其哈希值(Hash Value = 0)，确定其在位数组的中位置索引，然后取出该位置的值(即，BitArray[0])，其值为0，即说明元素”Tony”不存在于该Bloom Filter中

至此，Bloom Filter 模型的基本原理已经介绍完毕了。聪明的朋友可能已经发现了一个问题，即，发生哈希冲突可能会导致误判。假设我们现在对该Bloom Filter来判定元素”Wow”是否存在其中，其哈希值计算后，恰好为3。，从上图可知BitArray[3]=1，则那么根据上文介绍的判定规则，我们判定元素”Wow”存在于该Bloom Filter，显然该判定结果与该Bloom Filter中仅存在”Hello”、”World”两个元素的真实情况不符

因此正如前文所述，其是一种概率模型的数据结构，发生哈希冲突的概率可以减少，但是无法完全避免。故判定一个元素是否存在于Bloom Filter，如果判定结果是不存在(False)，则一定不存在；但是如果判定结果是存在(True)，则实际情况其实是可能存在，而不是一定存在，即假阳性。 所以，实际应用中，在Bloom Filter 一般会使用多个Hash Function，以减小发生哈希冲突的概率。即，减小误判率 P(true)。插入一个元素时，分别计算其在各个Hash Function的哈希值，然后将各个哈希值对应的Bit的值置1；而判定元素是否存在于Bloom Filter时，则要求各个哈希值对应的Bit的值均为1才行

现依然是已向一个Bloom Filter分别插入元素”Hello”、”World”为例，给出其插入过程的图解。不同的是，这次我们使用了2个Hash Function，并说明提高Hash Function个数如何降低误判率 P(true)

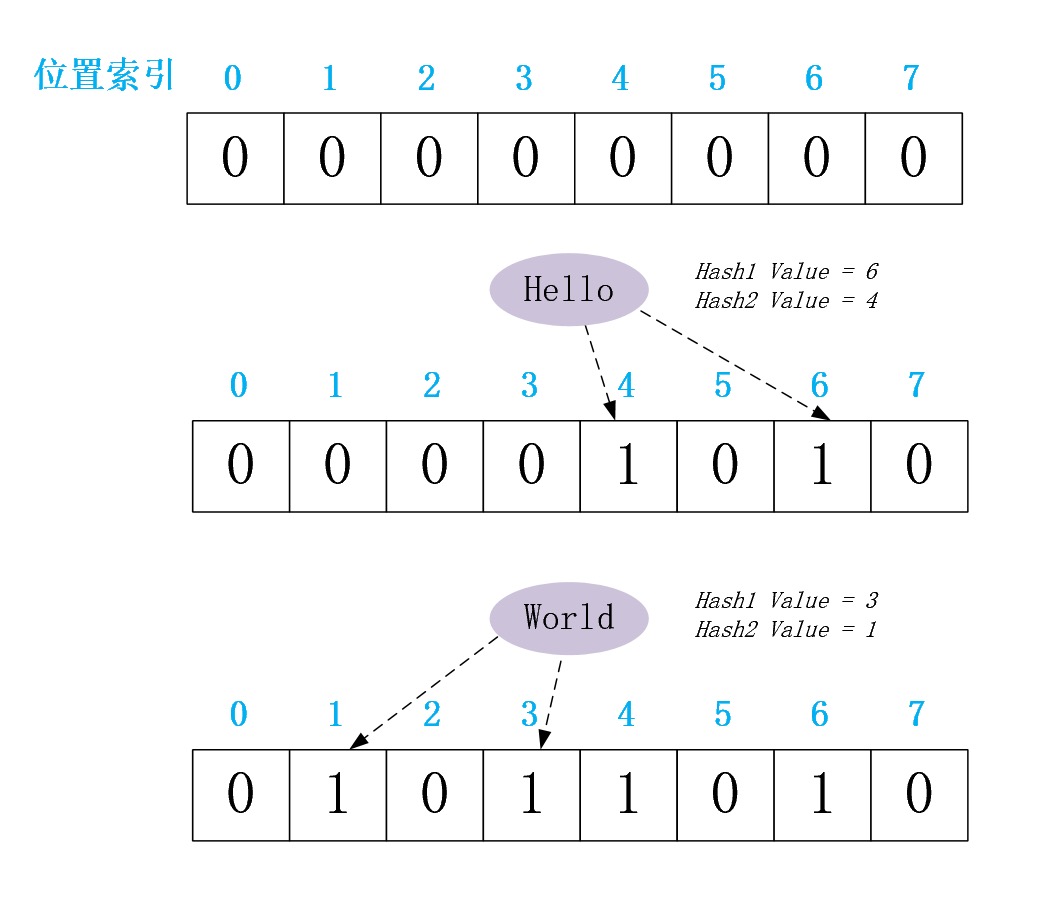
假设我们现在对该Bloom Filter依然判定元素”Wow”是否存在其中，其分别使用两个Hash Function计算哈希值，分别为3、0。从上图可知虽然BitArray[3]=1但是BitArray[0]=0，则那么根据上文介绍的判定规则，我们即可判定元素”Wow”不存在于该Bloom Filter。从这里，我们看出，提高Hash Function的个数可以显著降低误判率 P(true)

细谈参数设计

相信大家对于 Bloom Filter 的工作原理都有了一个基本的了解，现在我们来看看在Bloom Filter 中涉及到的一些参数指标：

• 欲插入Bloom Filter中的元素数目: n
• Bloom Filter误判率: P(true)
• BitArray数组的大小: m
• Hash Function的数目: k

欲插入Bloom Filter中的元素数目 n 是我们在实际应用中可以提前获取或预估的；Bloom Filter的误判率 P(true) 则是我们提前设定的可以接受的容错率。所以在设计Bloom Filter过程中，最关键的参数就是BitArray数组的大小 m 和 Hash Function的数目 k，下面将给出这两个关键参数的设定依据、方法

误判率 P(true)

向Bloom Filter插入一个元素时，其一个Hash Function会将BitArray中的某Bit置为1，故对于任一Bit而言，其被置为1的概率 $P_1=\frac{1}{m}$，那么其依然是0的概率 $P_0 = 1 - P_1 = 1- \frac{1}{m}$；易知插入一个元素时，其 $k$ 个Hash Function 都未将该Bit置为1的概率 $P_0^1 = ( 1- \frac{1}{m} )^k$。则向Bloom Filter 插入全部n个元素后，该Bit依然为0的概率即为 $P_0^n = ( 1- \frac{1}{m} )^{kn}$，反之，该Bit为1的概率则为 $P_1^n = 1- P_0^n = 1 - ( 1- \frac{1}{m} )^{kn}$

由前文可知，判定一个元素存在于Bloom Filter，要求k个Hash Function的哈希值对应的Bit的值均为1。据此，我们可以计算出其误判率 P(true)：

$$P(true) = (P_1^n)^k = [1 - ( 1- \frac{1}{m} )^{kn}]^k$$

根据基本极限

$$\lim_{x \to \infty} (1 - \frac{1}{x})^{-x} = e$$

可知：

$$P(true) \approx (1 - e^{-\frac{nk}{m}} )^k$$

从上式可以看出，当BitArray数组的大小m增大 或 欲插入Bloom Filter中的元素数目n 减小时，均可以使得误判率P(true)下降

Hash Function的数目 k

前文已经看到Hash Function数目k的增加可以减小误判率P(true)，但是随着Hash Function数目k的继续增加，反而会使误判率P(true)上升，即误判率是一个关于Hash Function数目k的凸函数。所以当k在极值点时，此时误判率即为最小值

$$f(k) = (1 - e^{-\frac{nk}{m}} )^k$$

令 $a = e^{\frac{n}{m}}$，则有：

$$f(k) = (1 - a^{-k} )^k$$

分别对上式两边，先取对数，再对k求一次导，可有：

$$\frac{1}{f(k)} f(k)^\prime = \ln( 1-a^{-k} ) + \frac{ k a^{-k} \ln a }{ 1-a^{-k} }$$

易知，当k取极值点时，有 $f(k)^\prime = 0$，故将其带入上式即可求出k

$$\ln( 1-a^{-k} ) + \frac{ k a^{-k} \ln a }{ 1-a^{-k} } = 0$$ $$\Rightarrow (1-a^{-k}) \ln( 1-a^{-k} ) = -k a^{-k} \ln a$$ $$\Rightarrow (1-a^{-k}) \ln( 1-a^{-k} ) = a^{-k} \ln a^{-k}$$ $$\Rightarrow 1-a^{-k} = a^{-k}$$ $$\Rightarrow a^{-k} = \frac{1}{2}$$ $$\Rightarrow e^{-\frac{kn}{m}} = \frac{1}{2}$$ $$\Rightarrow k = \frac{m}{n} \ln2 \approx 0.7\frac{m}{n}$$

此时，我们即可以利用上式的结果，通过m和n来确定最优的Hash Function数目k

BitArray数组的大小 m

如何确定BitArray数组的大小 m 呢？这里，我们联立 P(true)、k 的公式，即可解出 m

$$\begin{cases} P(true) = (1 - e^{-\frac{nk}{m}} )^k \\ k = \frac{m}{n} \ln2 \end{cases}$$

联立后有：

$$\Rightarrow P(true) = (1 - e^{-\ln2})^{\frac{m}{n}\ln2} = ( \frac{1}{2} ) ^ {\frac{m}{n} \ln2} \approx 0.6185^\frac{m}{n}$$

对上式求解，可得：

$$\Rightarrow \ln P(true) = \frac{m}{n} \ln2 \ln \frac{1}{2}$$ $$\Rightarrow m = - \frac{ n \ln P(true) }{ (\ln 2)^2 }$$

此时，我们即可以利用上式的结果，通过P(true)和n来确定最优的BitArray数组的大小 m

应用场景

1. 爬虫

由于互联网中的网页数量巨大，如果使用哈希表保存爬虫工具访问过的url显然是不现实的，此时即可使用Bloom Filter来存储。当爬虫工具每次爬取一个网页，判定该网页是否已经被爬取过时，如果Bloom Filter给出的是结果是False，则事实上一定没有被访问过，即可去爬虫；但如果Bloom Filter给出的是结果是True，即，该网页已经被爬取过。虽然有一定概率出现误判，即该网页其实并未被访问过。但是鉴于互联网中网页数目浩如烟海，遗漏很小一部分网页未被爬取访问在工程上也是可以接受的

2. 缓存穿透

缓存穿透：外部发送请求去查询一个缓存中一定不存在的数据。由于未命中缓存，则外部请求将直接转发到DB中，当外部频繁请求、流量过大时，即可能会直接导致DB服务宕机

同样地，这里可以应用Bloom Filter 来加在缓存前一级用于过滤查询请求，当判定查询数据不存在，即可直接返回请求而无需向缓存、DB传递该请求

参考文献

1. 《数学之美》 吴军著