xyZGHio

樱花同载酒，终似少年游

0%

浅谈判圈算法

发表于 更新于 阅读数： 评论数：
本文字数： 2.9k 阅读时长 ≈ 6 分钟

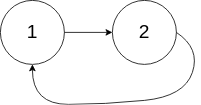
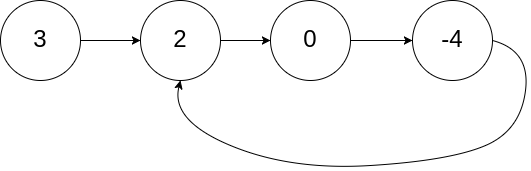
在计算机科学中，循环检测算法可用于判断状态机中是否存在循环、链表是否存在环等问题

abstract.jpeg

Floyd判圈算法

判断是否有环

该算法判断是否存在环的基本原理是分别使用快、慢指针进行遍历。其中，快指针每次走2步、慢指针每次走1步。如果两个指针相遇了，则说明存在环；反之，则不存在环

计算环的长度

当存在环时如何计算环的长度呢？其实也很简单。因为判断是否存在环的过程中，当快、慢指针相遇则说明这两个指针一定位于环当中了。故此时，只需使用其中任意一个指针按照每次走1步对环遍历一圈、进行计数即可

计算环的入口

这里令起始处为A、环的入口处为B，在判断是否有环阶段时快慢相遇之处为C。并记AB长度为a、记BC长度为b、环的长度为r。且在判断是否有环过程中，快指针每次走2步、慢指针每次走1步。则快、慢指针相遇时，快指针走过的长度是慢指针走过长度的2倍

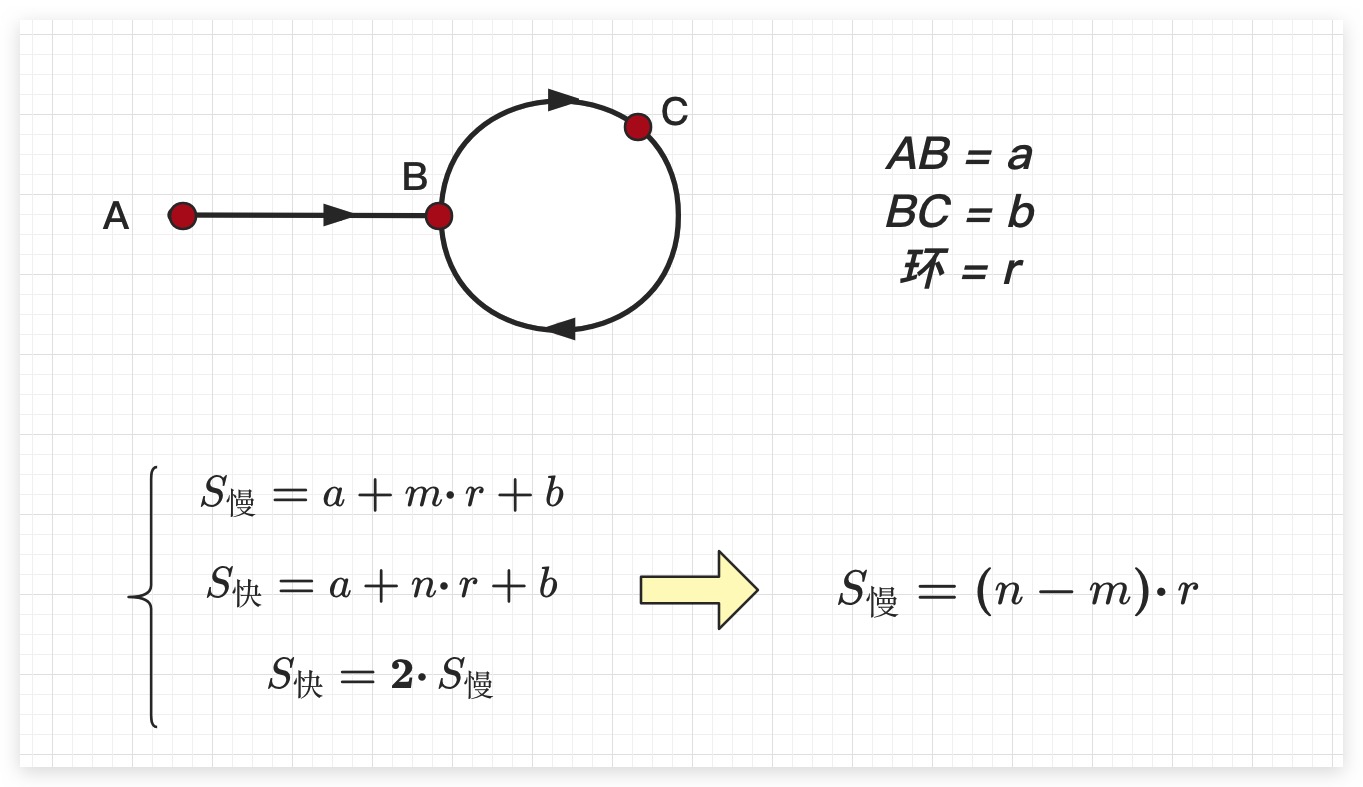
figure 1.jpeg

此时不难看出，当快、慢指针相遇时，快、慢指针走过的长度均是环长度的整数倍。故如果期望找到环的入口位置，即B处。则只需在两个指针相遇之时，将其中任意一个指针放置到起始处A，而另一个指针依然位于相遇处C。然后两个指针按照每次均走1步的速度向前走，当二者再次相遇之时，即是B处

原因在于，对于相遇后继续往前走的指针而言，由于其已经走过了若干圈环的长度，此时只需再走a步即可到达环的入口。这个地方换个角度想会更容易理解，如果该指针先走a步再走若干圈环的长度，其必然位于环的入口处；而对于相遇后从起始处A开始走的指针而言，其显然走a步后，必然也会位于环的入口处。故此时两个指针第二次相遇之时，说明他们均已经走完a步。即到达环的入口处

Brent判圈算法

Brent判圈算法相比较于Floyd判圈算法来说，其重点在于提高了判断是否有环的时间效率。该算法并没有解决计算环的长度、找出环的入口这两个问题。具体地，该算法同样会使用两个指针：快、慢指针。当两个指针相遇则说明存在环。具体地，快指针每次始终只会走1步。只不过，第1轮时快指针累计最多只能走2步，第2轮时快指针累计最多只能走4步，第3轮时快指针累计最多只能走8步,以此类推。而慢指针则是在每一轮结束后，直接移动到快指针的位置处

实践

判断是否有环

学习过程中要善于理论联系实际。故在介绍完Floyd判圈算法、Brent判圈算法的基本原理后，现在我们来进行实践。这里以LeetCode的第141题——环形链表 为例

给你一个链表的头节点head，判断链表中是否有环
如果链表中有某个节点，可以通过连续跟踪next指针再次到达，则链表中存在环。如果链表中存在环，则返回 true。否则，返回 false

示例 1：

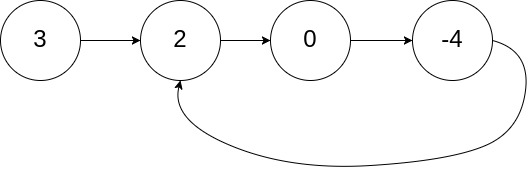
figure 2.png

输入：head = [3,2,0,-4]
输出：true
解释：链表中有一个环，其尾部连接到第二个节点

示例 2：
figure 3.png
输入：head = [1,2]
输出：true
解释：链表中有一个环，其尾部连接到第一个节点

示例 3：
figure 4.png
输入：head = [1]
输出：false
解释：链表中没有环

则基于Floyd判圈算法版本的实现如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * Floyd Algo
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = slow;
        while ( fast!=null && fast.next!=null ) {
            slow = slow.next;
            fast = fast.next.next;
            if( slow==fast ) {
                return true;
            }
        }
        return false;
    }
}

则基于Brent判圈算法版本的实现如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Brent Algo
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = slow;
        // 快指针每轮过程中最多走几步
        int limit = 2;
        // 记录快指针在每轮过程中走的步数
        int step = 0;
        
        while ( fast!=null && fast.next!=null ) {
            // 快指针每次走1步
            fast = fast.next;
            step++;

            // 判断快、慢指针是否相遇, 即是否存在环
            if( fast == slow ) {
                return true;
            }

            // 开启新一轮的同时, limit变为原来的2倍, 同时将慢指针移动到快指针的位置上
            if( step==limit ) {
                step = 0;
                limit = limit * 2;
                slow = fast;
            }
        }

        return false;
    }
}

计算环的入口

学习过程中要善于理论联系实际。故在介绍完Floyd判圈算法、Brent判圈算法的基本原理后，现在我们来进行实践。这里以LeetCode的第141题——环形链表 II 为例

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。不允许修改链表

示例 1：
figure 5.png
输入：head = [3,2,0,-4]
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点

示例 2：
figure 6.png
输入：head = [1,2]
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点

示例 3：
figure 7.png
输入：head = [1]
输出：返回 null
解释：链表中没有环

根据上文对计算环的入口的说明，不难写出以下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode entry = null;
        boolean hasCycle = false;

        ListNode slow = head;
        ListNode fast = head;
        while ( fast!=null && fast.next!=null ) {
            slow = slow.next;
            fast = fast.next.next;
            if( slow==fast ) {
                // 检测到环
                hasCycle = true;
                break;
            }
        }

        // 存在环时, 则计算环的入口
        if( hasCycle ) {
            // 快指针放置到链表开始处
            fast = head;
            // 快、慢指针每次1步同时移动
            while ( true ) {
                // 快、慢指针再次相遇, 即为环的入口
                if( fast==slow ) {
                    entry = fast;
                    break;
                }
                fast = fast.next;
                slow = slow.next;
            }
        }

        return entry;
    }
}
推荐文章
请我喝杯咖啡捏～

欢迎关注我的微信公众号：青灯抽丝