本文谈一谈在计算机科学和数学领域中的经典问题——约瑟夫环问题

问题描述

据说著名犹太历史学家Josephus有过以下的故事：在罗马人占领乔塔帕特后，39 个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus和他的朋友并不想遵从。Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置。这样当所有犹太人全部自杀后，他和他的朋友就逃过了这场死亡游戏

上面这个故事可以看作是约瑟夫问题的由来。其核心内容就在于：N个人围成一圈，第一个人从1开始依次进行报数。当报到M时将该人杀掉。然后从被杀掉的下一个人开始，重新从1继续报数。直到只剩下最后一个人。试问最终存活下来的人是谁？事实上LeetCode的剑指Offer(第2版)题单中的第62题——圆圈中最后剩下的数字，即是一个约瑟夫环问题

0,1,···,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字（删除后从下一个数字开始计数）。求出这个圆圈里剩下的最后一个数字。例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3

示例 1
输入: n = 5, m = 3
输出: 3

示例 2：
输入: n = 10, m = 17
输出: 2

链表模拟法

这里我们以解决上述LeetCode原题为例，说明如何利用链表模拟法解决该问题。在该方法中我们通过一个链表来模拟这个过程，每次删除第M个元素，直到链表中最终只剩下一个元素为止。示例代码如下所示。同时在计算下一个被杀人的编号时，为了实现环的特性。我们通过对链表长度进行取模实现即可

/**
 * 链表模拟法: 非递归版本
 */
class Solution2 {
    public int lastRemaining(int n, int m) {
        List<Integer> list = new ArrayList<>();
        for(int i=0; i<n; i++) {
            list.add(i);
        }

        int index = 0;
        while ( list.size()>1 ) {
            int removeIndex = (index + m -1) % list.size();
            list.remove( removeIndex );
            index = removeIndex;
        }

        return list.get(0);
    }
}

数学法

虽然模拟法易懂，但在时间复杂度上的表现却乏善可陈。事实上对于约瑟夫环问题而言，其是有数学解法的。这里我们定义一个函数F(N,M)：其表示在N个人的环每次杀掉第M个人后，最终活下来的人的编号。这里我们以N=4、M=2为例，如下图所示

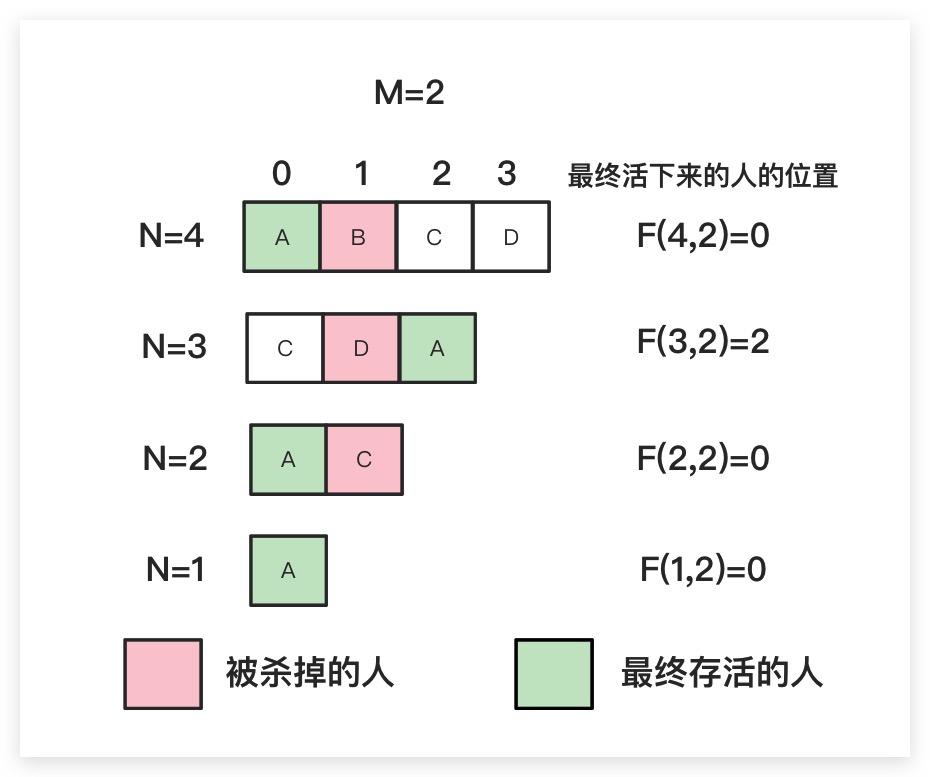
可以看到当N为1时，我们知道最终存活下来的人是A。显然此时位置一定为0，即F(1,2)=0。事实上，对于任何M均存在F(1,M)=0。那问题来了，我们如何通过F(N-1, M)计算出F(N,M)呢？通过图解的形式观察A在每轮杀人过程中的位置。不难看出N=3时A在2位置，即F(3,2)=2；N=4时A在0位置，即F(4,2)=0。这里我们以N=3推导出N=4为例说明

首先N=4时将被杀掉的B补回数组的末端
再向数组整体向右移动M=2个单位，显然此时A的位置变为4了
但不难看出此时数组发生了溢出。故为了实现环的操作特性。我们需要将数组溢出的部分填充到最前面，表现在代码上就是通过取模实现

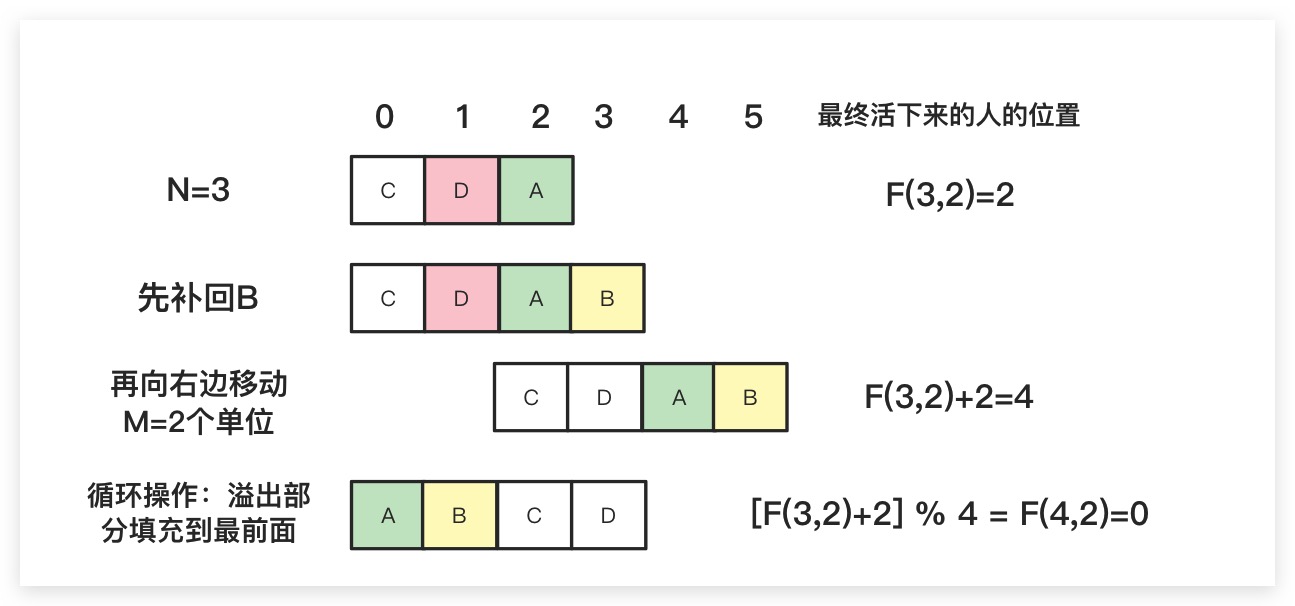
通过分析F(3,2)到F(4,2)的过程，很容易得到：F(4,2) = [F(3,2)+2] % 4。进而有：

当N>1时: F(N,M) = [F(N-1,M) + M] % N
当N=1时: F(N,M) = 0

/**
 * 数学法
 */
class Solution {
    public int lastRemaining(int n, int m) {
        int res = 0;
        for(int i=2; i<=n; i++) {
            res = (res+m) % i;
        }
        return res;
    }
}

xyZGHio

浅谈约瑟夫环问题

问题描述

链表模拟法

数学法