Radix Sort 基数排序是对计数排序的改进，该算法可以支持针对浮点、字符串等类型元素进行排序。其主要思想是将排序元素按数位分割依次排序，从而实现整体有序。其同样可以具有线性时间的性能

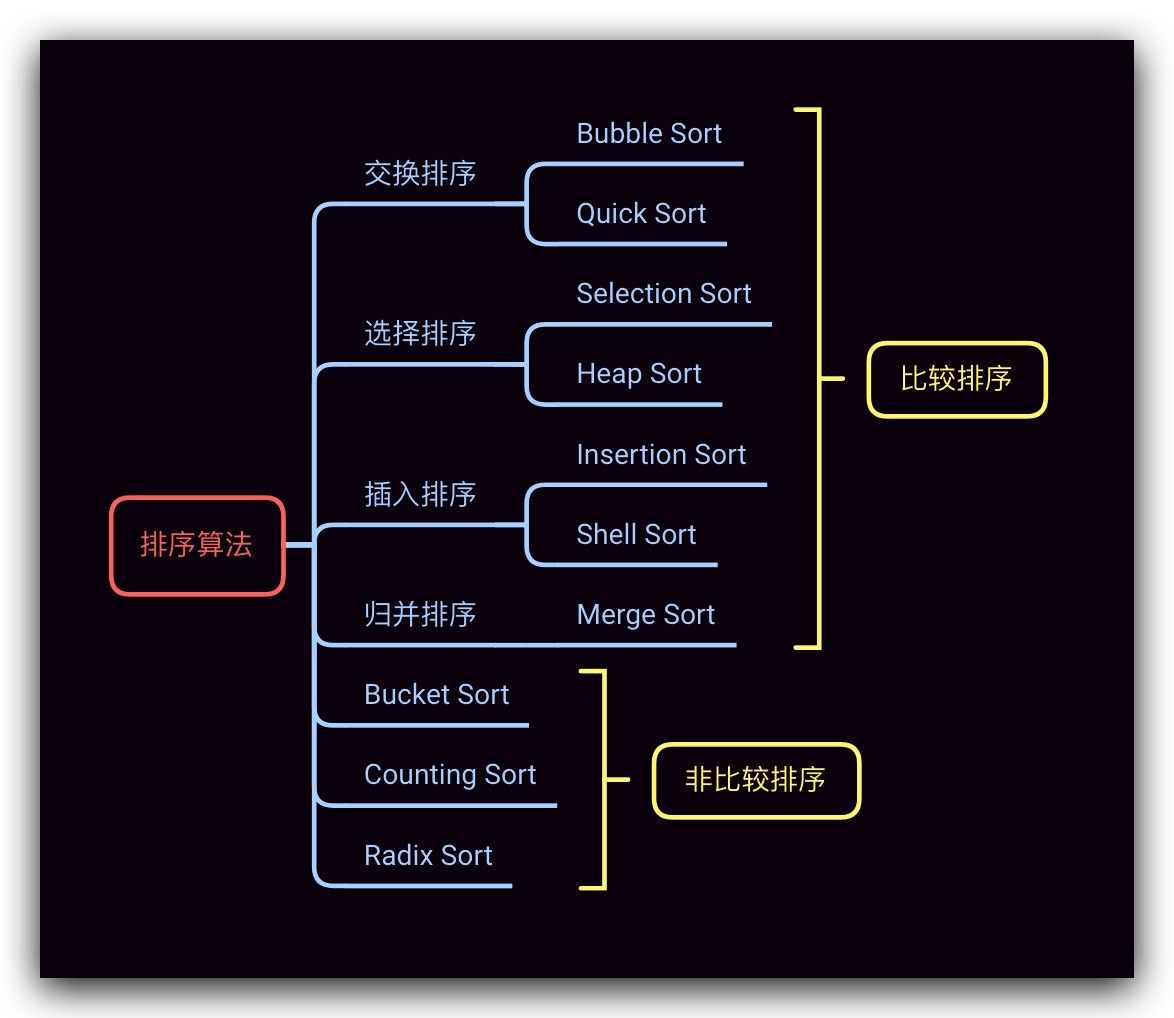
基本原理

在对非负整数进行基数排序时，需要首先将排序元素统一为相同的数位长度，数位不足的排序元素可以添加前导零的方式实现数位长度统一对齐；然后从排序元素的最低位（个位）开始进行排序，直到完成对最高位的排序，此时即实现了对排序元素的整体排序。而对每个数位进行排序的过程则是通过（稳定的）计数排序完成的，故基数排序同样是稳定的。由于我们是从排序元素的最低位向最高位依次排序的，故这种方式被称为最低位（LSD，Least Significant Digit）法；反之，如果是从排序元素的最高位向最低位依次排序的，则被称之为最高位（MSD，Most Significant Digit）法

实际上，基数排序算法对排序元素的类型不要求一定是非负整数才可以进行，其对于字符串、浮点数等类型均可适用。其关键在于要求排序元素的数位长度统一。例如对整数排序时，如果排序元素中含有负数，则可以对排序元素均加上一个数使其全部为非负整数；如果元素类型是字符串的话，在计数排序过程中，可以直接使用该位字符对应ASCII码值进行计数，对于长度不足的字符串，可直接在其后面补0实现长度对齐。即在计数排序过程中，如果发现某位字符是为对齐所填充的0的话，则可认为其对应的ASCII码值为0进行计数，因为字符’A’所对应的ASCII码值是65，字符’0’所对应的ASCII码值是48，均比0大。这样即可保证基数排序的结果是符合字典序的

实现

这里是一个通过Java实现的对非负整数类型的元素进行基数排序的实例，来帮助大家更好地理解该算法

/**
 * 基数排序
 */
public class RadixSort {
    /**
     * 升序排列
     */
    public static void sort() {
        int[] array = getTestCase();    // 获取测试用例
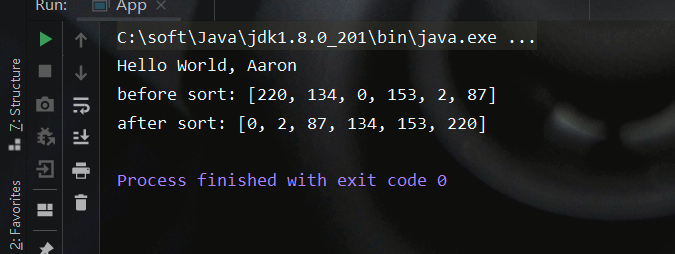
        System.out.println("before sort: " + Arrays.toString(array) );
        array = radixSortByLSD(array);
        System.out.println("after sort: " + Arrays.toString(array) );
    }

    /**
     * 基数排序: LSD(最低位)法
     */
    private static int[] radixSortByLSD(int[] array) {
        int radix = 10;     // 基数（数位的取值范围为[0,9]）
        int size = array.length;
        int[] sortedArray = new int[size];  // 排序结果数组

        // 计算待排序元素的最大位数 d
        int maxDigits = -1;
        for(int element : array ) {
            maxDigits = Math.max( getDigits(element), maxDigits);
        }

        // 从最低位开始遍历排序(计数排序)直到最高位为止
        for(int i=1; i<=maxDigits; i++) {
            // 对元素指定位i上的数进行计数排序
            int[] counts = new int[radix]; // 创建次数统计数组
            // 统计次数
            for(int element : array) {
                // 获取排序元素第i位上的数
                int num = getNumberByIndex(element, i);
                counts[num]++;
            }
            // 计算统计数组的累加值
            for(int j=1; j<radix; j++) {
                counts[j] = counts[j-1] + counts[j];
            }
            // 倒序遍历排序数组，保证稳定性
            for(int j=size-1; j>=0; j--) {
                // 获取排序元素第i位上的数
                int num = getNumberByIndex(array[j], i);
                // 该排序元素在对第i位进行计数排序后的排序位置, 因为数组索引从0开始计算，故应对排序位置减1
                int sortIndex = counts[num]-1;
                // 将原数组元素放入排序后的位置上
                sortedArray[sortIndex] = array[j];
                // 下一个重复的元素，应排前一个位置，以保证稳定性
                counts[num]--;
            }
            array = sortedArray.clone();    // 本次排序结果用于下一次计数排序
        }
        return array;
    }

    /**
     * 计算整数位数
     * @param num
     * @return
     */
    private static int getDigits(int num) {
        if(num==0) {
            return 1;
        }
        int digits = (int)Math.log10(num) + 1;
        return digits;
    }

    /**
     * 取出num中某一数位上的数
     * @param num
     * @param index 1: 个位; 2: 十位; 3: 百位...
     * @return
     */
    private static int getNumberByIndex(int num, int index) {
        int digits = getDigits(num);
        if(index>digits) {
            return 0;   // num不足指定位数，则使用前导零填充
        }
        int numInIndex = num / (int)Math.pow(10, index-1) % 10;
        return numInIndex;
    }

    /**
     * 获取测试用例
     */
    private static int[] getTestCase() {
        int[] caseArray = {220, 134, 0, 153, 2, 87};
        return caseArray;
    }
}

测试结果如下：

特性

N为排序元素的数目，r为基数，d为排序元素的最大位数（长度）。当d为常数且r=O(N)时，其具有线性时间复杂度

参考文献

算法导论 · 第3版
计算机程序设计艺术(第3卷)：排序与查找高德纳(Donald E.Knuth) 著

xyZGHio

排序算法(八)：Radix Sort 基数排序

基本原理

实现

特性

参考文献