基本排序算法中的插入排序虽然逻辑较为简单，但当排序规模较大时，经常需要将元素一位一位地从一端移动到另一端，效率非常低。于是Donald Shell设计了一种基于插入排序的改进版排序算法，故被命名为 Shell Sort 希尔排序

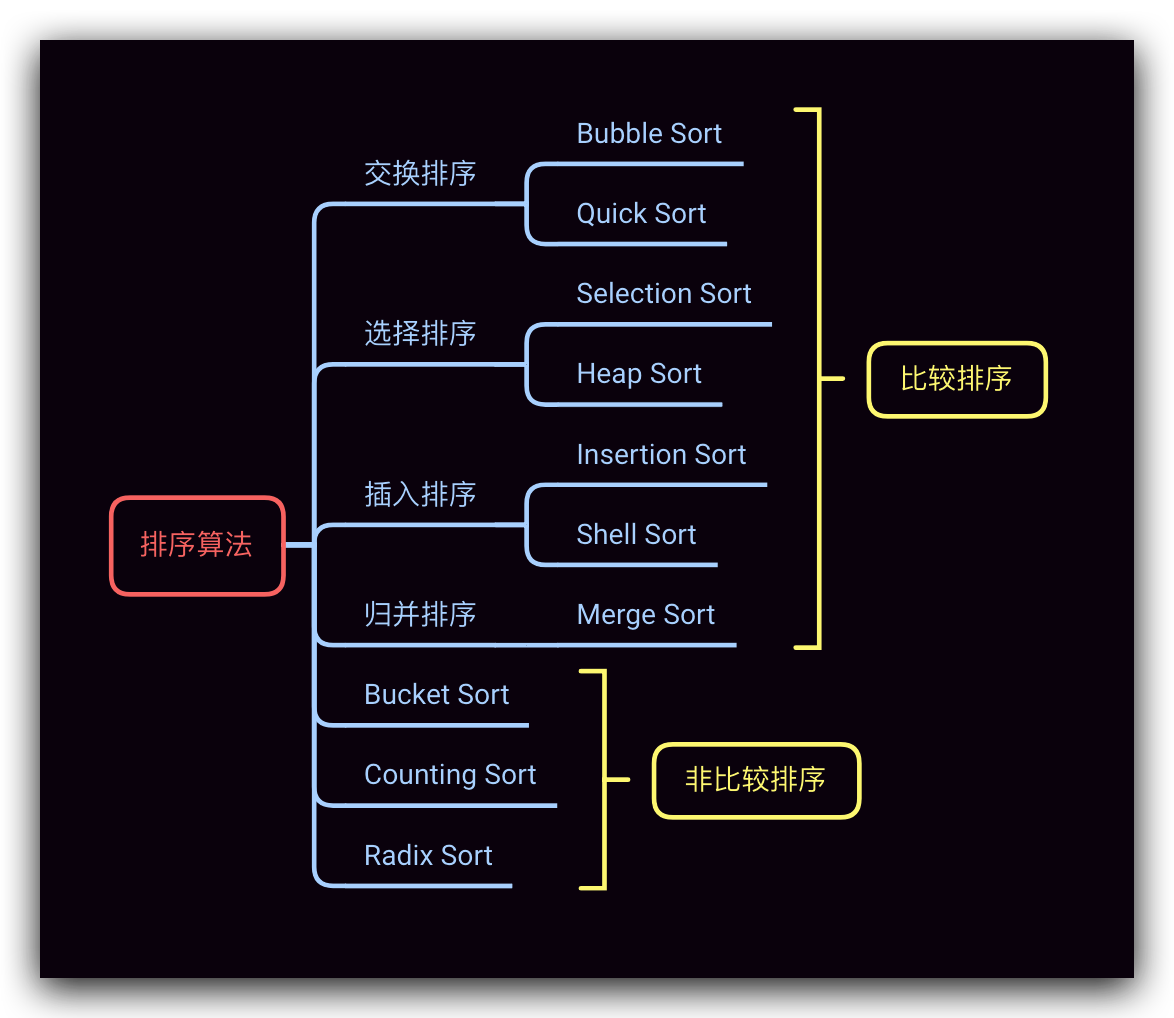
算法思想

插入排序效率低下是因为其移动元素每次只能移动一位，当排序元素的规模较大时，需要将元素一位一位地从一端移动到另一端。而如果我们能够让元素一次性地移动到较远的位置上，这样无疑就可以避免多次一位一位地移动操作。希尔排序正是基于此原理来优化、提高插入排序的效率。通过指定步长step，将原数组分为step个互相独立子数组，然后通过插入排序对这些子数组分别进行排序(即分组排序)，这时我们称其为step有序数组。当step很大时，我们就可以将元素一次性移动到很远的位置上，为下一次较小的step有序创造便利；不断缩小步长step，重复上述过程建立step有序数组，达到局部有序的目的。当step最终为1做最后一次step有序时，就是我们平常所熟悉的插入排序了，由于该数组已经多次被较大的step进行分组排序了，此时只需要较少次数的元素移动就可以实现整个数组全局有序

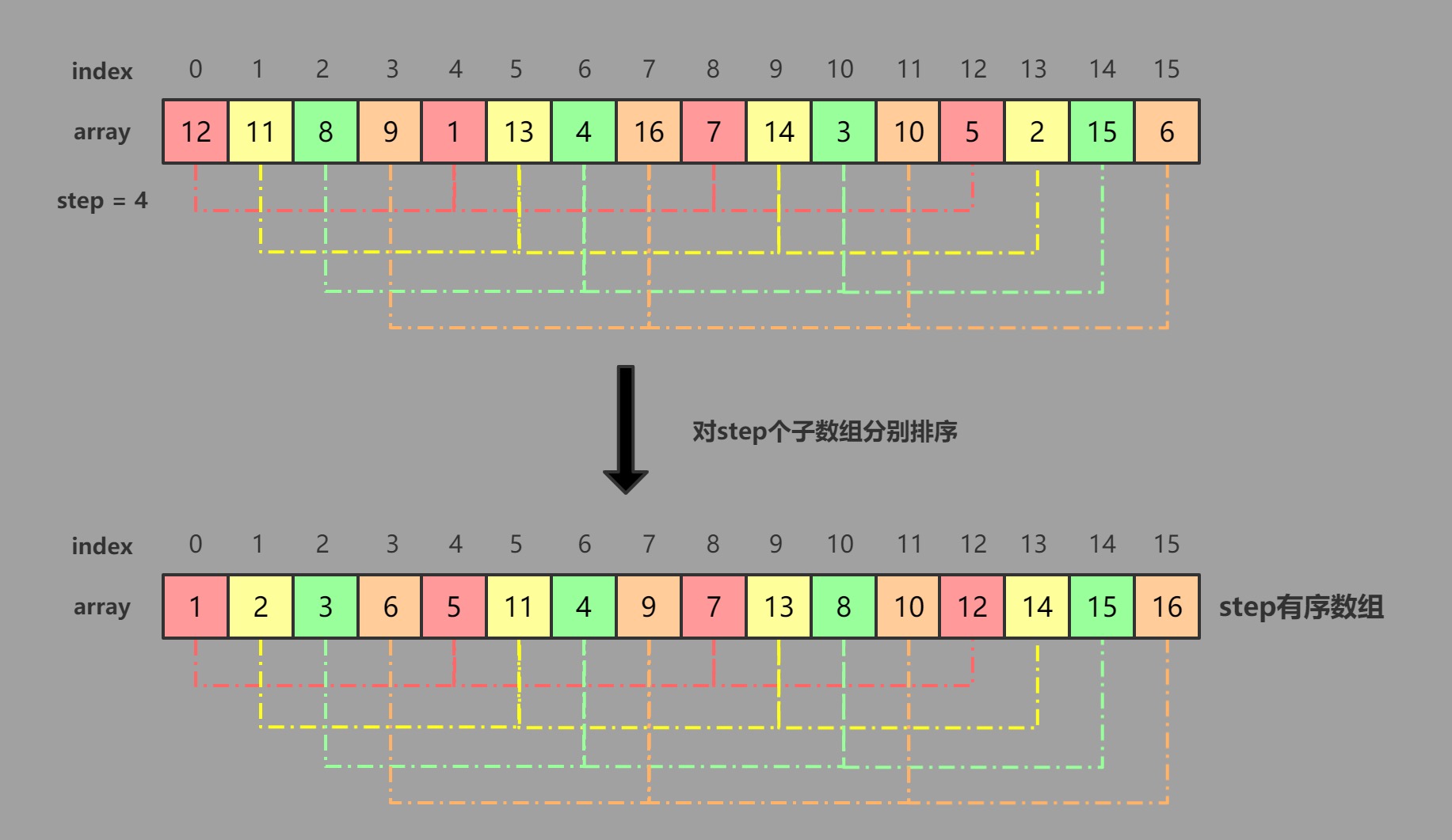
在希尔排序中，需要经历若干次step有序。在每一次step有序过程中，分组所使用的step步长越来越小直到其为1，即其是一个最后项为1的递减序列。关于step序列的选取问题，不建议大家自行设计，这里给出一个合适并简单的step序列的通项公式。在实际使用时，根据排序规模计算到合适的第n项，然后将该数列反序。即为我们进行希尔排序时所用到的step序列

$\mathrm{step}( \mathrm{n} ) = \frac{1}{2}(3^\mathrm{n}-1), (\mathrm{n} \ge 1)$

Java 代码示例

这里即是一个希尔排序的示例

/**
 * 希尔排序
 */
public class ShellSort {
    /**
     * 升序排列
     */
    public static void sort() {
        int[] array = getTestCase();
        int size = array.length;

        System.out.println("before sort: " + Arrays.toString(array) );

        int step = 1;   // 希尔排序的步长
        // 根据排序规模计算step序列到第n项
        while( step < size/3 ) {
            step = 3 * step + 1;    // step(n) = 1/2*(3^n-1) 的递推公式
        }

        while( step>=1 ) {
            // 按指定步长step进行分组，对array[i]进行排序，使之step有序
            for( int i=step; i<size; i++ ) {
                // 将array[i]插入到array[i-step],array[i-2*step],array[i-3*step]...当中
                for(int j=i; j-step>=0 && less(array[j],  array[j-step]); j-=step ) {
                    exchange(array, j, j-step);
                }
            }
            // 更新步长
            step = step/3;
        }

        System.out.println("after sort: " + Arrays.toString(array) );
    }

    /**
     * 判定a是否比b小
     * @param a
     * @param b
     * @return
     */
    private static boolean less(int a, int b) {
        if(a<b) {
            return true;
        }
        return false;
    }

    /**
     * 交换数组中 i、j 位置的元素
     * @param array
     * @param i
     * @param j
     */
    private static void exchange(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

    /**
     * 获取测试用例
     */
    private static int[] getTestCase() {
        int[] caseArray = {-54,12,16,44,36,99,2,88,5,33,26,4,64,3,-44,-2,62,71,27,10,49,83,92};
        return caseArray;
    }
}

测试结果如下：

特性

空间复杂度

由于希尔排序是原地排序算法，故其空间复杂度为O(1)

时间复杂度

希尔排序的时间复杂度很大程度取决于step序列的设计，故此在前文中不建议大家自行设计step序列。对于本文所给出的step序列，其时间复杂度不超过平方阶。就到底什么样的step序列是最优的，目前该问题依然无解。但我们可以知道的是，在中等规模的排序需求中，一般情况下直接使用希尔排序已经足够了。如果经实际测试确实需要优化，此时再考虑使用快排等排序算法也不迟

稳定性

不稳定

参考文献

算法(第4版) Robert Sedgewick、Kevin Wayne 著
计算机程序设计艺术(第3卷)：排序与查找高德纳(Donald E.Knuth) 著

xyZGHio

排序算法(五): Shell Sort 希尔排序

算法思想

Java 代码示例

特性

空间复杂度

时间复杂度

稳定性

参考文献