现代基础性计算环境中，输入量的元素规模N会非常大，但有时候会只要求从中找出K个最大(或最小)的元素，即Top K问题。如果使用之前介绍的传统排序算法，先对N个元素进行全排序然后再取前K个元素，计算代价会变的非常高昂。因为我们实际上只需要Top K元素的排序，而剩余元素的详细排序结果我们其实并不care。而本文介绍的Heap Sort堆排序不仅是一种高效的排序算法，还可以很好地解决Top K问题

二叉堆

定义

堆 Heap, 一种特殊的树状数据结构。在堆中，对于任意节点都有其值恒大于等于或小于等于其子节点的值，前者称之为max heap最大堆，后者则称之为min heap最小堆。常见的堆有:二叉堆、多叉堆、斐波那契堆等。这里我们所使用的即是二叉堆，其在形式上是一个完全二叉树

一般地，我们通过数组来实现二叉堆，将堆中元素按从上到下、从左到右的层级顺序依次存储到数组中即可(一般地为简便起见，通常从数组的第二个位置开始存储元素，不使用数组索引为0的位置。故大小为N的堆，所需数组的空间大小为N+1)。下图即为一个最大堆的存储示意图(为简便起见，下文中的”堆”均特指”二叉堆”)

在一个堆中，对于位置为k节点，根据上图可知，其父节点在数组中的位置索引为 floor(k/2)，其两个子节点在数组中的位置索引分别为2*k、2*k+1

堆有序化

一个堆可能会由于某种原因打破其本来的有序状态，此时就需要重新调整来恢复、保证堆的有序状态，这个调整恢复的过程就称之为堆的有序化

堆有序:当一颗二叉树的任意节点恒大于等于或小于等于其两个子节点时，即被称为堆有序

本文我们以最大堆为例进行介绍，最小堆与其大同小异，此处将不再赘述。具体地，当一个堆的根节点元素被较小的元素替换时，我们就需要自上而下地恢复堆的有序化；当向堆底插入一个新节点时，我们则需要自下而上地恢复堆的有序化

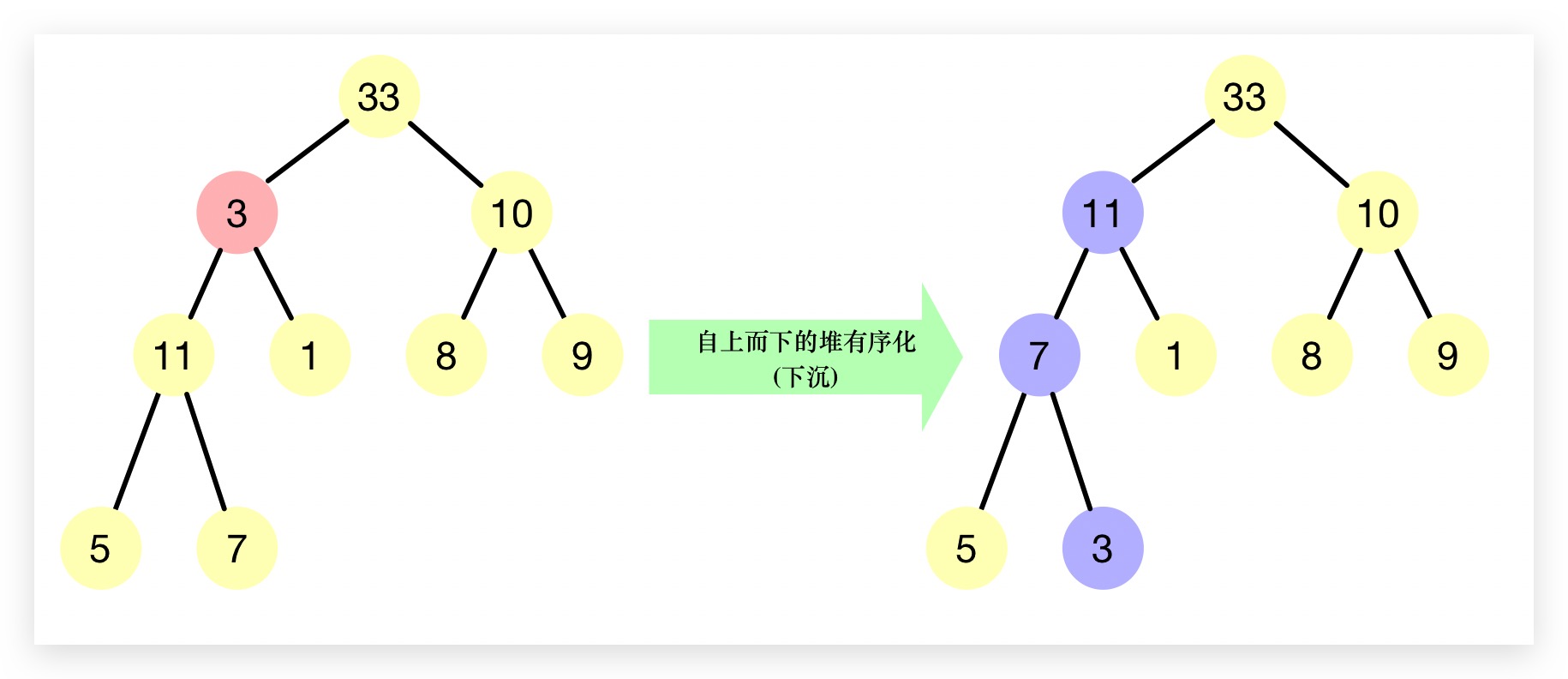
1. 自上而下的堆有序化(下沉)

当一个最大堆的有序状态因为某个节点比其(两个或其中一个)子节点更小而被打破时，那么可以通过将该节点与其两个子节点中的较大者交换来恢复堆，该过程形象化地被称为”下沉”。交换后，可能会导致其在子节点处依然会继续打破堆的有序化，故我们需要不断地使用相同的方式将其进行修复，将节点向下移动直到其子节点均比其更小或到达了堆的底部。下图即是一个值为3的节点通过”下沉”恢复堆的有序化的过程

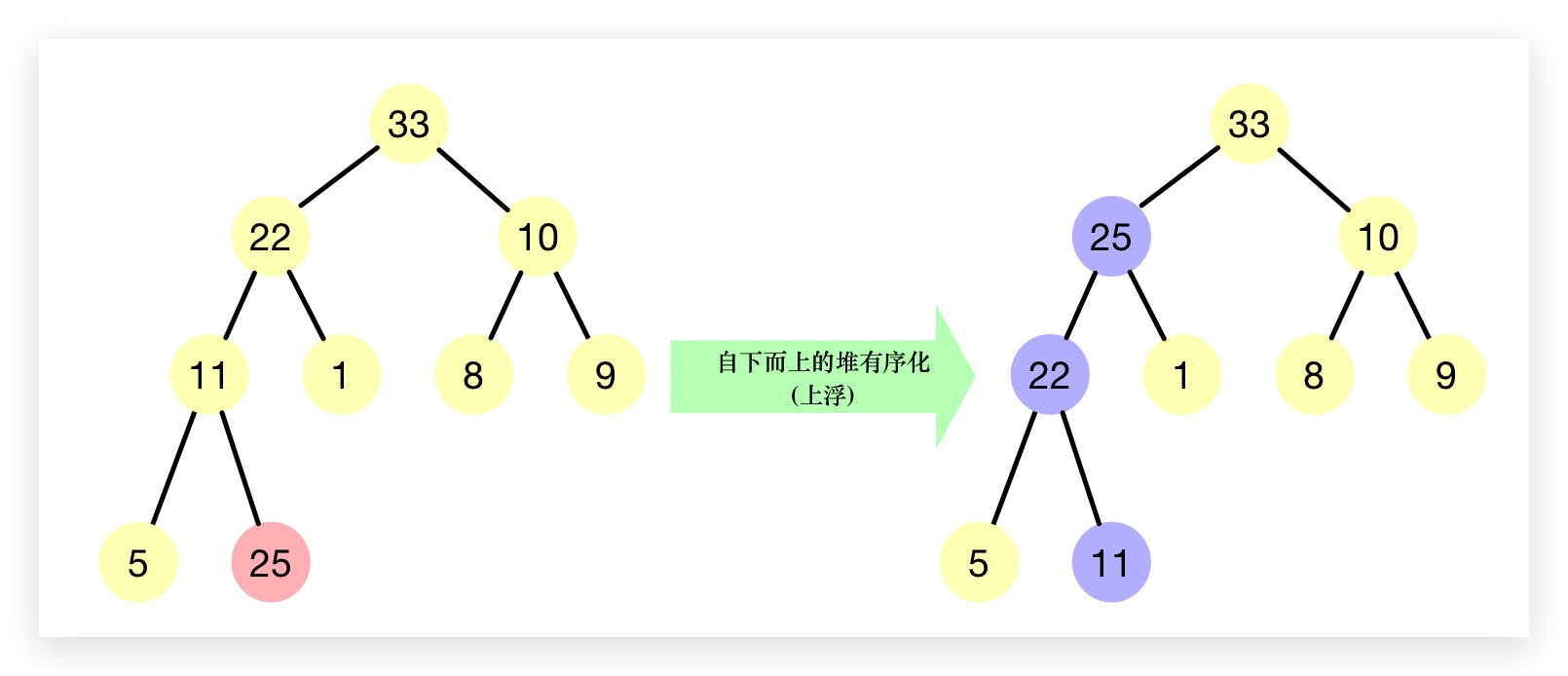
2. 自下而上的堆有序化(上浮)

当一个最大堆的有序状态因为某个节点比其父节点更大而被打破时，那么可以通过将该节点与其父节点交换来恢复堆，该过程形象化地被称为”上浮”。交换后，可能会导致其在父节点处依然会继续打破堆的有序化，故我们需要不断地使用相同的方式将其进行修复，将节点向上移动直到其父节点节点比其更大或成为了堆的根节点。下图即是一个值为25的节点通过”上浮”恢复堆的有序化的过程

Java 实现

Java的ArrayList是一个自动扩容的动态数组列表，故可用其实现最大堆。实现代码如下所示

/**
 * 堆排序
 */
public class HeapSort {

    /**
     * 最大堆
     */
    private static ArrayList<Integer> maxHeap;

    /**
     * 获取堆的大小
     * @return
     * @apiNote 大小为N的堆，其数组大小为N+1
     */
    private static int getSize() {
        return maxHeap.size()-1;
    }

    /**
     * 上浮, 自下而上的堆有序化
     */
    private static void swim(int k) {
        // 第 k 个元素不是根节点 且 比父节点大
        while ( k>1 && oneLTtwo(k/2,k) ) {
            swap(k, k/2);   // 交换当前节点与父节点位置, 将当前节点上浮一层
            k = k/2;
        }
    }

    /**
     * 下沉, 自上而下的堆有序化
     * @param k
     * @param N 堆的大小
     */
    private static void sink(int k, int N) {
        while( 2*k <= N ) {    // 该节点存在(左)子节点
            int childIndex = 2 * k; // 该节点下较大子节点的索引
            // 该节点存在右子节点 且 左子节点小于右子节点
            if( childIndex<N && oneLTtwo(childIndex, childIndex+1) ) {
                childIndex++;
            }
            // 当前节点 不小于 子节点，则停止下沉
            if(! oneLTtwo(k, childIndex)) {
                break;
            }
            swap(k, childIndex);    // 交换当前节点与较大子节点位置, 将当前节点下沉一层
            k = childIndex;
        }
    }

    /**
     * 交换两个元素
     * @param indexA
     * @param indexB
     */
    private static void swap(int indexA, int indexB) {
        int elementA = maxHeap.get(indexA);
        int elementB = maxHeap.get(indexB);
        maxHeap.set(indexA, elementB);
        maxHeap.set(indexB, elementA);
    }

    /**
     * 第一个元素 是否小于 第二个元素
     * @param indexA
     * @param indexB
     * @return
     */
    private static Boolean oneLTtwo(int indexA, int indexB) {
        if( maxHeap.get(indexA) < maxHeap.get(indexB) ) {
            return true;
        }
        return false;
    }

}

Heap Sort 堆排序

算法思想

通过上文，我们知道构造一个大小为N的最大堆，我们就可通过根节点获取N个元素中最大的元素。这里我们以对N个元素进行升序排列为例，讲解堆排序的算法思想：

将N个元素构造成一个最大堆，其中array[0]位置不使用
从一个大小为N的最大堆中将根节点(N个元素中最大的元素)array[1]从堆中移出，放入数组最后的位置中，则array[N]元素排序完成
对剩下的大小为N-1的最大堆，重新进行堆的有序化: 将堆底元素array[N-1]放入根节点的位置array[1]，并通过”下沉”重现建立新堆的有序化
重复上述Step 2-3，直到最大堆中只剩一个元素时为止。此时N个元素即排序完成

从上可以看出，堆排序实际上也是选择排序的一种，其通过堆的特性每次选取最大(或最小)的元素完成排序

Java实现

通过上文我们知道，在进行堆排序前，我们首先要用N个元素建立一个最大堆。一般地做法是，对待排序数组按从左到右的顺序进行遍历，依次从堆底添加新元素，通过”上浮”的方式来完成一个大小为N的堆的建立。然而更高效的做法是，我们从堆的最后一个父节点开始从右往左、从下而上，依次通过”下沉”父节点的方式完成堆的构建。因为当一个父节点的两个子堆都是有序时，此时在该父节点上调用”下沉”方法，即可将它们变成一个堆。前者需要N次”上浮”才能将元素一个一个地添加到堆中以此来完成堆的构建；而后者则只需floor(N/2)次”下沉”即可将堆构建完成，因为一个大小为N的完全二叉树，叶子节点的数量至少为N/2个

/**
 * 堆排序
 */
public class HeapSort {

    /**
     * 最大堆
     */
    private static ArrayList<Integer> maxHeap;

    /**
     * 升序排列
     */
    public static void sort() {
        // 获取测试用例
        Integer[] array = getTestCase();
        maxHeap = new ArrayList<>();
        maxHeap.add(null);  // 在索引为0上添加空元素, array[0]位置不使用
        maxHeap.addAll( Arrays.asList(array) );

        System.out.println("before sort: " + Arrays.toString(array) );

        // 通过下沉的方式构造最大堆
        int N = getSize();  // 最大堆大小
        for(int i=N/2; i>0; i--) {
            sink(i, N);
        }

        // 堆排序, 升序排列
        while (N>1) {
            swap(1, N); // 将当前堆的最大元素(根节点)从堆中移除, 放入正确的排序位置
            N--;    // 更新当前最大堆的大小
            sink(1, N); // 对于剩余堆进行有序化
        }
        // 移除索引为0上的空元素
        maxHeap.remove(0);

        System.out.println("after sort: " + maxHeap );
    }

    /**
     * 获取堆的大小
     * @return
     * @apiNote 大小为N的堆，其数组大小为N+1
     */
    private static int getSize() {
        return maxHeap.size()-1;
    }

    /**
     * 获取测试用例
     */
    private static Integer[] getTestCase() {
        Integer[] caseArray = {3,7,10,1,4,9,8,5,2,6};
        return caseArray;
    }
}

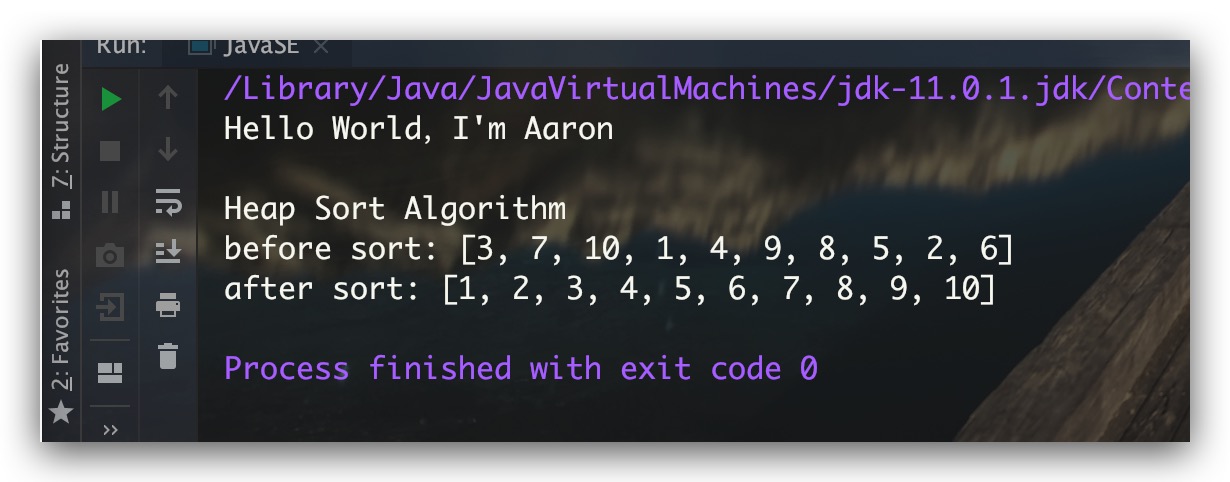
测试结果如下:

特性

时间复杂度(average)	时间复杂度(worst)	时间复杂度(best)	空间复杂度	稳定性
$O(N \log N)$	$O(N \log N)$	$O(N \log N)$	$O(1)$	不稳定

Top K 问题

定义

Top K 问题：从N个元素中找出最大(或最小)的K个元素

解决方案

容易想到的是解决方案是，对N个元素进行排序，然后根据排序结果从中取出最大(或最小)的K个元素，但是当N的规模非常之大时，效率会非常低。而堆则可以很好解决地该问题。这里，我们以取出最小的K个元素为例，说明如何通过最大堆解决该问题(若是找出最大的K个元素，则应通过最小堆解决):

建立一个最大堆，遍历N个元素并重复下述 Step 2-3
若堆的大小未达到K时，直接将新元素放入堆底，然后通过”上浮”恢复堆的有序化
若堆的大小已经为K时，则比较根节点元素(即堆中最大元素)是否比新元素大。若是，则直接用新元素来替换该堆的根节点，并通过”下沉”恢复堆的有序化；若不是，则直接丢弃该新元素即可
当N个元素全部遍历完成后，此时堆中元素即为所要找出最小的K个元素

Java 实现

这里利用Java实现一个从N个元素找出最小的K个元素的Demo

/**
 * 堆排序
 */
public class HeapSort {

    /**
     * 最大堆
     */
    private static ArrayList<Integer> maxHeap;

    /**
     * (Top K 问题) 取K个最小的元素
     */
    public static void TopK() {
        Integer[] array = getTestCase();

        System.out.println("Input Array: " + Arrays.toString(array) );

        int K = 3;
        maxHeap = new ArrayList<>();
        maxHeap.add(null);  // 在索引为0上添加空元素, array[0]位置不使用

        for(int i = 0; i<array.length; i++) {
            int size = getSize();  // 最大堆大小
            if( size < K ) {    // maxHeap 未填满
                maxHeap.add( array[i] );    // 从后面追加插入新元素
                swim(size+1);   //上浮, 对堆自下而上的有序化
            } else {            // maxHeap 已填满
                Integer maxElement = maxHeap.get(1);    // 获取堆中最大的元素
                if( array[i] < maxElement ) {   // 新元素比堆中最大的元素还小
                    maxHeap.set(1, array[i]);   // 替换根节点元素
                    sink(1, size);      // 下沉, 对堆自上而下的有序化
                }
            }
         }

        // 移除索引为0上的空元素
        maxHeap.remove(0);
        System.out.println("Top " + K + " (Min) : " + maxHeap );
    }

    
    /**
     * 获取测试用例
     */
    private static Integer[] getTestCase() {
        Integer[] caseArray = {3,7,10,1,4,9,8,5,2,6};
        return caseArray;
    }

}

测试结果如下:

参考文献

算法(第4版) Robert Sedgewick、Kevin Wayne 著
计算机程序设计艺术(第3卷)：排序与查找高德纳(Donald E.Knuth) 著

xyZGHio

排序算法(四): Heap Sort 堆排序与 Top K 问题

二叉堆

定义

堆有序化

Java 实现

Heap Sort 堆排序

算法思想

Java实现

特性

Top K 问题

定义

解决方案

Java 实现

参考文献