排序算法(三): Quick Sort 快速排序

之前的文章中，我们介绍了Merge Sort算法，其时间复杂度虽然是线性对数的，但是由于辅助数组的存在，致使其空间复杂度为线性的。那有没有一种排序算法，能够在时间、空间上都表现较为良好均衡呢？答案是有的，这就是在各种库中广泛使用的 Quick Sort 快速排序，简称”快排”

切分过程详解

切分目的

快速排序，和归并排序算法一样，亦运用了分治的思想在里面。归并排序是先对两个子数组分别排序，然后将两个有序的子数组归并在一起以使整个数组有序；而快速排序虽然也是先将待排序数组通过切分操作一分为二的分为两个子数组，但是当这两个子数组分别排序、有序之后，整个数组即已经是排序完成的了。下图即是一个将数组切分后再分别对子数组升序排序的图解

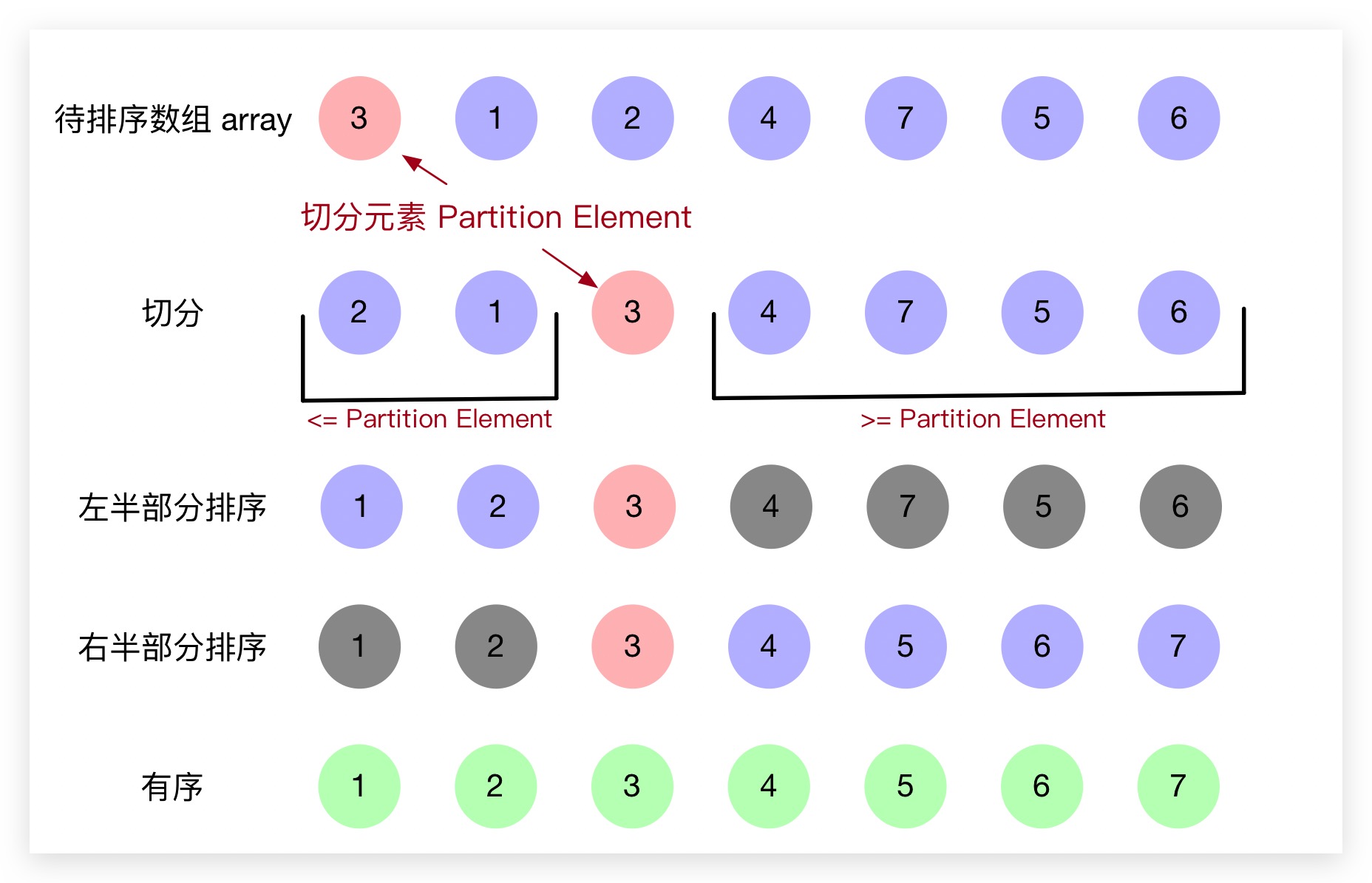
结合上图可以看出，其切分时，先从待排序数组中随机选取一个元素(记为切分元素)，当切分操作完成时，必须保证数组中切分元素的左侧元素均不大于它、切分元素的右侧元素均不小于它。即，通过快速排序的切分过程，我们实际上是完成了对切分元素的排序工作。故，当左、右两半部分元素分别有序后(可通过递归调用切分实现)，整个数组自然而然就是有序状态

切分原理

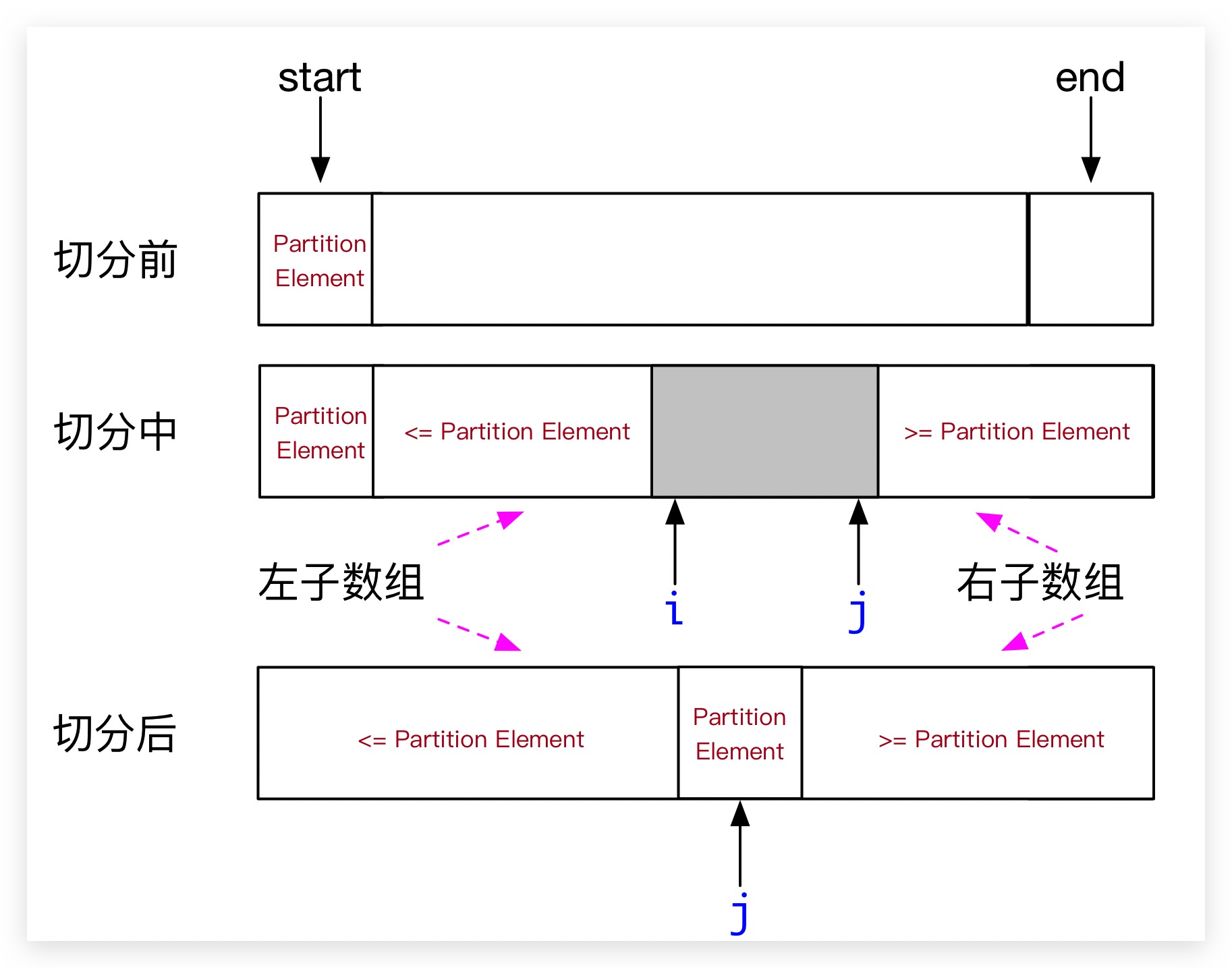
从上文我们知道了切分的作用及目的，现在我们结合下图来看看切分的原理。一般地，我们随机地使用数组的第一个元素作为切分元素Partition Element——即切分后排序完成的元素。然后从数组的左端开始向右扫描,直到找到一个大于等于切分元素的元素；再从数据的右端开始向左扫描，直到找到一个小于等于切分元素的元素；然后交换array[i]、array[j]这两个元素。重复上述的”扫描-交换”过程，即可保证：游标i左侧的元素均不大于切分元素Partition Element、游标j右侧的元素均不小于切分元素Partition Element。当两个游标i、j相遇时，我们只需将切分元素array[start]与左子数组最右侧的元素(a[j])交换，即完成切分，此时切分元素array[start]即完成排序，位置索引即为j

Java 实现

这里以Java为例实现了一个用于数组array升序的切分方法partition()

/**
 * 对数组指定范围的元素进行切分操作，并返回切分点 j
 * 使之满足 array[start]~array[j-1] <= array[j] <= array[j+1]~array[end]
 * @param array 待排序数组
 * @param start 起点
 * @param end 终点
 * @return
 */
private static int partition(int[] array, int start, int end) {
    int i = start;      // 左游标
    int j = end + 1;    // 右游标
    int partitionElement = array[start];    //  切分元素

    while (true) {
        // 左游标从左向右扫描, 查找不小于切分元素的元素
        while ( array[++i] < partitionElement ) {
            if( i>=end ) {  // 边界检查
                break;
            }
        }
        // 右游标从右向左扫描, 查找不大于切分元素的元素
        while ( array[--j] > partitionElement ) {
            if( j<=start ) {    // 边界检查
                break;
            }
        }
        // 左、右游标相遇,即扫描结束
        if( i>=j ) {
            break;
        }
        swap(array, i, j);
    }
    swap(array, start, j);  // 将切分元素放入正确的位置, 即 array[j] 排序完成
    return j;   // 返回切分点, array[start]~array[j-1] <= array[j] <= array[j+1]~array[end]
}
/**
 * 交换数组元素
 * @param array
 * @param indexA
 * @param indexB
 */
private static void swap(int[] array, int indexA, int indexB) {
    int temp = array[indexA];
    array[indexA] = array[indexB];
    array[indexB] = temp;
}

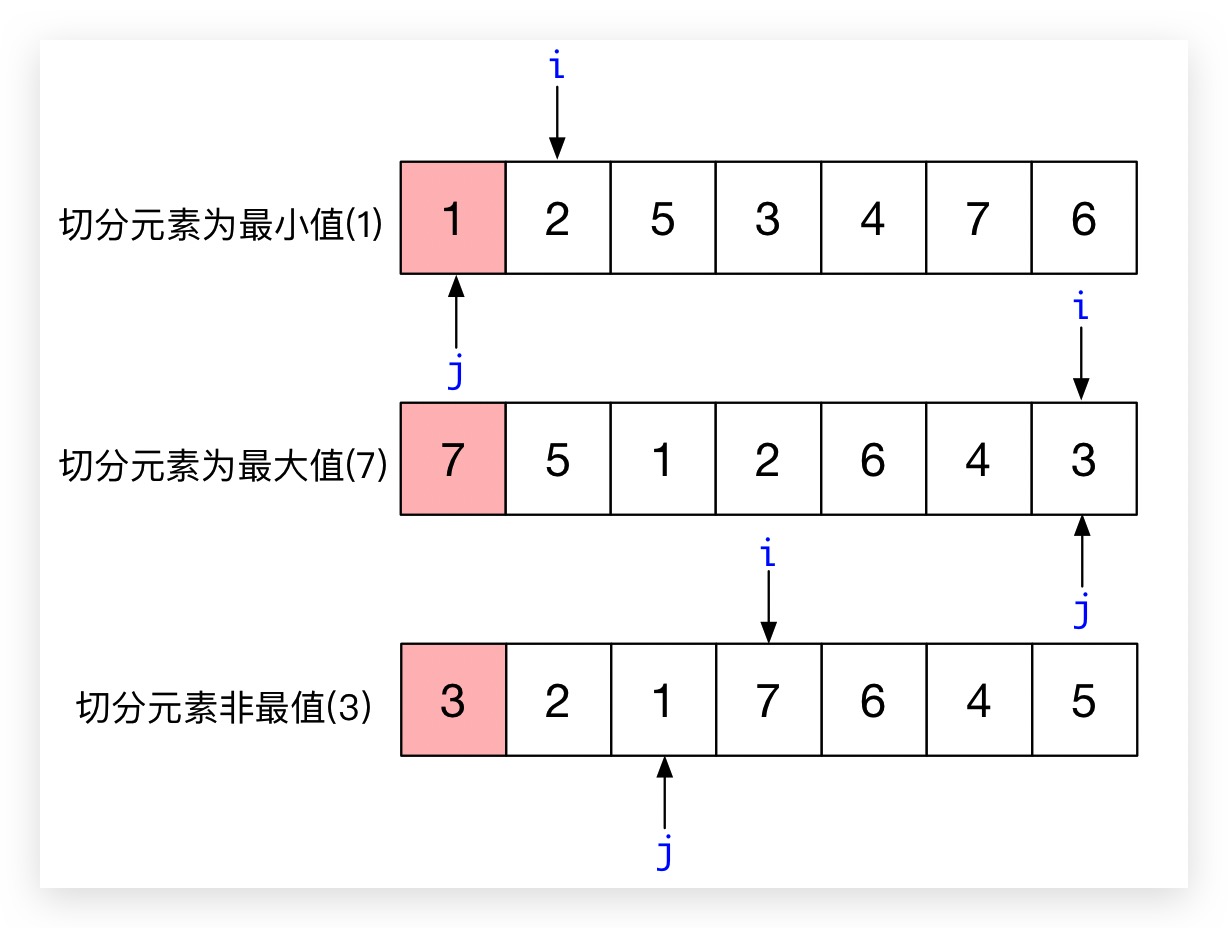
有些人看完代码会有一个疑问，为什么”扫描-交换”过程完成之后，左子数组最右侧的元素位置是array[j]，即,切分元素的排序位置为什么就是j呢？这里，我们分别以切分元素为最小值、最大值、非最值三种情况为例，计算一下”扫描-交换”完成后i、j游标的数值，通过观察下图即可看出切分元素的排序位置恰好是j

基础快速排序

算法思想

上文我们详细分析了快速排序中的关键操作——切分。现在，我们来看看快速排序算法的思想：要对数组排序，需先对欲排序数组进行切分，获取切分点(记为j)，根据切分点即可将原数组一分为二：左子数组(array[start]~array[j-1])、右子数组(array[j+1]~array[end])，再通过递归的方式分别对左、右子数组进行切分、排序。即可完成对整个数组的排序

Java 实现

现通过Java代码实现快速排序（partition方法实现在上文已给出，此处不再赘述）

/**
 * 快速排序
 */
public class QuickSort {
    /**
     * 升序排列
     */
    public static void sort1() {
        int[] array = getTestCase();
        int size = array.length;

        System.out.println("before sort: " + Arrays.toString(array) );

        sort(array, 0, size-1);

        System.out.println("after sort: " + Arrays.toString(array) );
    }

    /**
     * 对数组指定范围的元素进行升序排列
     * @param array 待排序数组
     * @param start 起点
     * @param end 终点
     */
    private static void sort(int[] array, int start, int end) {
        if( start >= end ) {
            return;
        }
        int partitionIndex = partition(array, start, end); // 切分并返回切分点j, 此时array[j]排序完成
        sort( array, start, partitionIndex-1 ); // 对左子数组 array[start]~array[j-1] 进行排序
        sort( array, partitionIndex+1, end);    // 对右子数组 array[j+1]~array[end] 进行排序
    }
    
    /**
     * 获取测试用例
     */
    private static int[] getTestCase() {
        int[] caseArray = {3,7,10,1,4,9,8,5,2,6};
        return caseArray;
    }
}

测试结果:

特点

时间复杂度(average)	时间复杂度(worst)	时间复杂度(best)	空间复杂度	稳定性
$O(N \log N)$	$O(N^2)$	$O(N \log N)$	$O(\log N)$	不稳定

从上表可以看出快速排序的平均时间复杂度是线性对数级别，而空间复杂度是对数级别，较我们之前介绍的排序算法而言，时间、空间耗费均较为平衡。故在有些语言的默认排序方法即是通过快排实现

值得一提的是，该算法非常脆弱。因为切分后理想的切分点应是在正中间的位置，而如果待排序数组是有序的。那么每次切分时，再选数组中第一个元素作为切分元素，则其切分点位置恰好都是在数组的两端，此时既为最坏的情况——即时间复杂度为平方级别，为最大程度避免出现该情况。在实际应用中，可以通过以下两点进行优化:

• 保证随机性 : 排序前先将元素打乱；每次任意地选取不同位置上的元素作为切分元素
• 处理与切分元素相等的元素情况 : 在上文的”扫描-交换”过程，左游标是遇到一个大于等于切分元素的元素停下；右游标是遇到一个小于等于切分元素的元素停下。虽然这样处理可能会导致一些不必要的元素交换，但可以一定程度上避免切分点过于靠近数组的两端

基于三向切分的快速排序

当待排序元素中包含大量重复元素时，基础快速排序算法实际上会对重复元素每一个均会进行切分、排序。而如果我们在切分的过程中，按小于、等于和大于切分元素这三个分类来切分，可以大大提高快速排序的效率，可将时间复杂度从线性对数降至线性级别

原理

我们通过游标i从左到右遍历整个数组，同时分别维护一个左游标lt、右游标gt。使得左游标lt左侧元素(array[start] ~ array[lt-1])均小于切分元素，右游标gt右侧元素(array[gt+1] ~ array[end])均大于切分元素。而在 array[lt] ~ array[i-1] 中的元素均等于切分元素，array[i] ~ array[gt] 中的元素则待遍历、分类。三向切分图解如下图所示，当三向切分完成时，array[lt] ~ array[gt] 中的元素均等于切分元素，即绿色部分已经排序完成，只需对蓝色部分(小于切分元素)、黄色部分(大于切分元素)递归完成排序即可

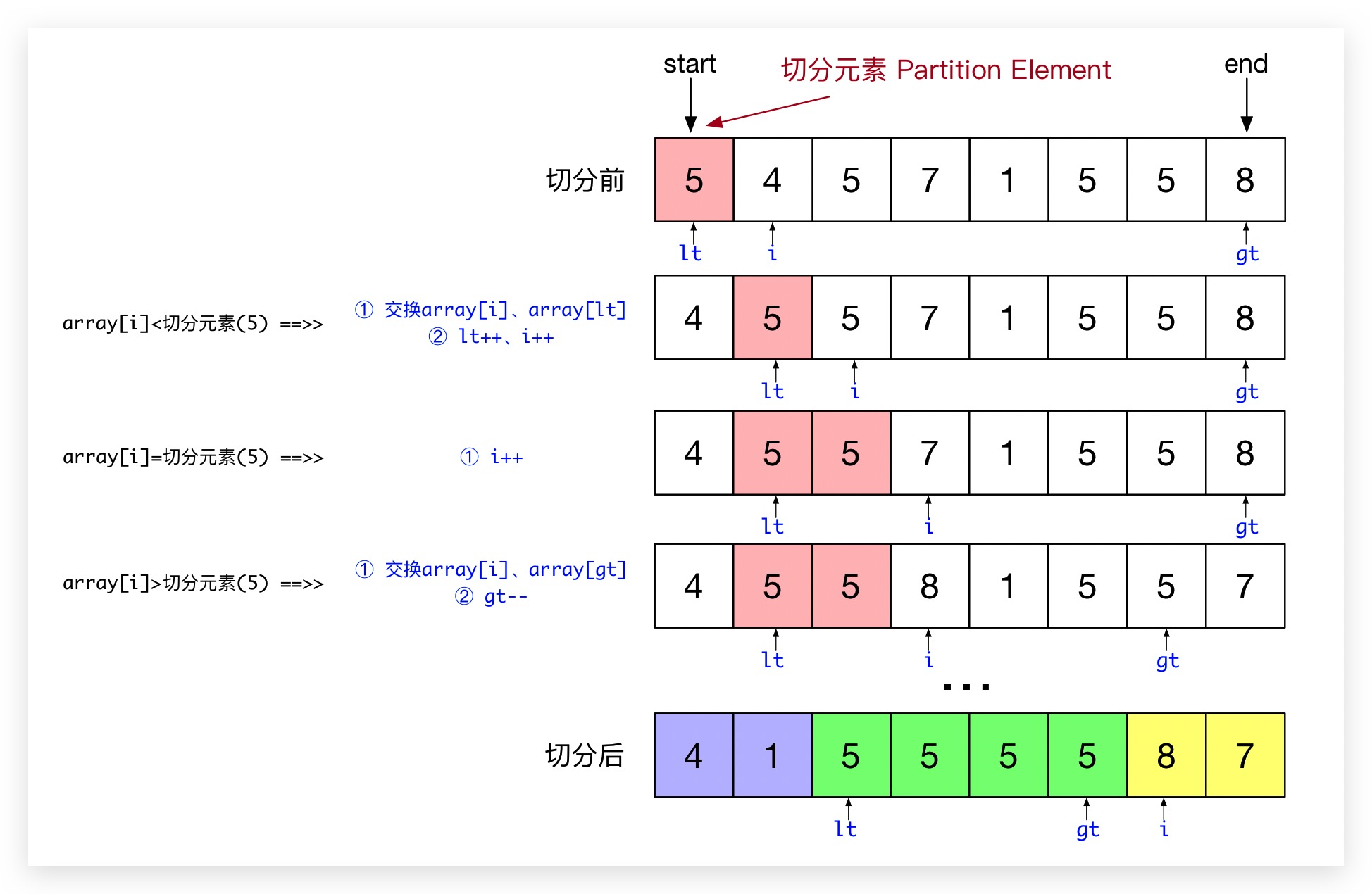
Java 实现

现通过Java代码实现基于三向切分的快速排序

/**
 * 快速排序
 */
public class QuickSort {
    /**
     * 升序排列(使用三向切分)
     */
    public static void sort2() {
        int[] array = getTestCase();
        int size = array.length;

        System.out.println("before sort: " + Arrays.toString(array) );

        sortBy3Way(array, 0, size-1);

        System.out.println("after sort: " + Arrays.toString(array) );
    }
    /**
     * 三向切分
     * @param array
     * @param start
     * @param end
     */
    private static void sortBy3Way(int[] array, int start, int end) {
        if( start >= end ) {
            return;
        }

        int partitionElement = array[start];    //  切分元素
        int lt = start;     // 游标 lt 左侧元素 均小于 切分元素
        int gt = end;       // 游标 gt 右侧元素 均大于 切分元素
         int i = start+1;    // 遍历游标
        // 三向切分，使得下式结果成立
        // array[start]~array[lt-1] < array[lt]~array[gt] = partitionElement < array[gt+1]~array[end]
        while ( i<=gt ) {
            if( array[i] > partitionElement) {  // 大于切分元素,则将其放置在 gt 游标右侧
                swap(array, i, gt);
                gt--;
            } else if (array[i] < partitionElement) {   // 小于切分元素,则将其放置在 lt 游标左侧
                swap(array, i, lt);
                lt++;
                i++;
            } else {    // 等于切分元素, 则无需改变其位置
                i++;
            }
        }
        sortBy3Way(array, start, lt-1);     // 对左子数组 array[start]~array[lt-1] 进行排序
        sortBy3Way(array, gt+1, end);       // 对右子数组 array[gt+1]~array[end] 进行排序
    }
    /**
     * 获取测试用例
     */
    private static int[] getTestCase() {
        int[] caseArray = {5,4,5,7,1,5,5,8};
        return caseArray;
    }
}

测试结果:

特点

时间复杂度(average)	时间复杂度(worst)	时间复杂度(best)	空间复杂度	稳定性
$O(N \log N)$	$O(N^2)$	$O(N)$	$O(\log N)$	不稳定

参考文献

1. 算法(第4版) Robert Sedgewick、Kevin Wayne 著