Hough Transform 霍夫变换之直线检测

在图像处理中，经常需要找出一个平面上散点集中可能存在的直线，即直线检测。比较容易想到的办法是选取任意两个散点并计算其所在直线方程的k、b系数对；遍历全部散点两两计算，则出现频率较高的直线方程k、b系数对，即是图像中存在的直线。但是该方法过于暴力，当散点集规模较大时，效率十分低下。而通过 Hough Transform 霍夫变换则可以大大提高对散点集中存在的直线的检测效率

Hough Transform 霍夫变换

笛卡尔坐标系下的参数空间

我们知道笛卡尔坐标系下，直线方程为y=kx+b。现在我们对该直线方程变形后有 b=-kx+y，这时我们不再把k、b看作是系数，而是将其分别作为参数空间的自变量、因变量，而x、y则看作是系数。这样我们就可以实现笛卡尔坐标系与其参数空间之间的映射

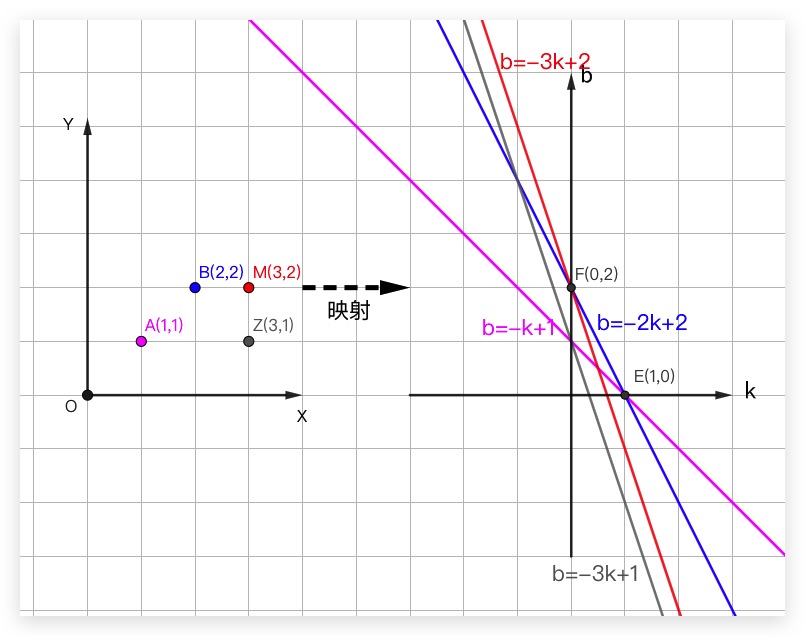
可以看到笛卡尔坐标系下的点A、B、M映射到参数空间中实际上是线，而笛卡尔坐标系中的直线AB、直线BM映射到参数空间中实际上是点E、F。即霍夫空间的对偶性。但由于垂直于X轴的直线，其斜率k无穷大、不存在，所以会导致点M、Z在参数空间中对应的线是平行的，没有交点，即该参数空间下无法描述k不存在的直线

极坐标系下的参数空间

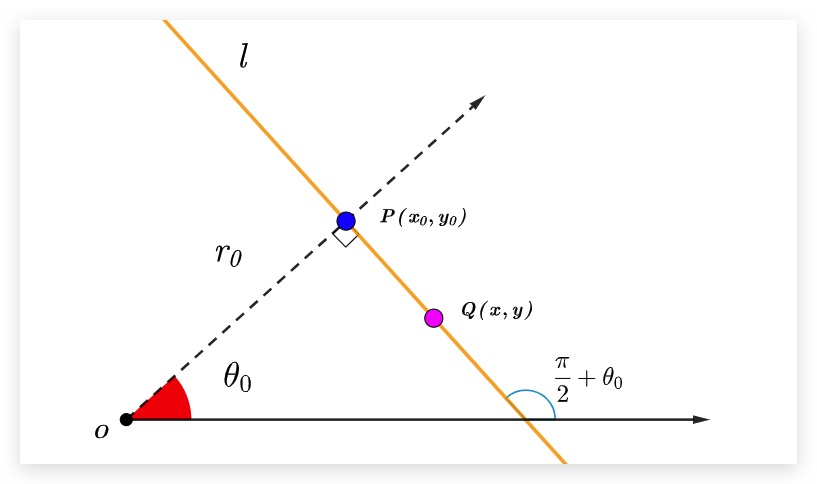
直线l在极坐标系下的方程如下所示:

$$\rho(\theta) = r_0 * \sec(\theta - \theta_0)$$

则对于直线l上任意一点Q而言，我们有:

联立(1)、(2)式，可求得点Q在极坐标系下的参数空间方程

这样我们就可以实现极坐标系与参数空间之间的映射

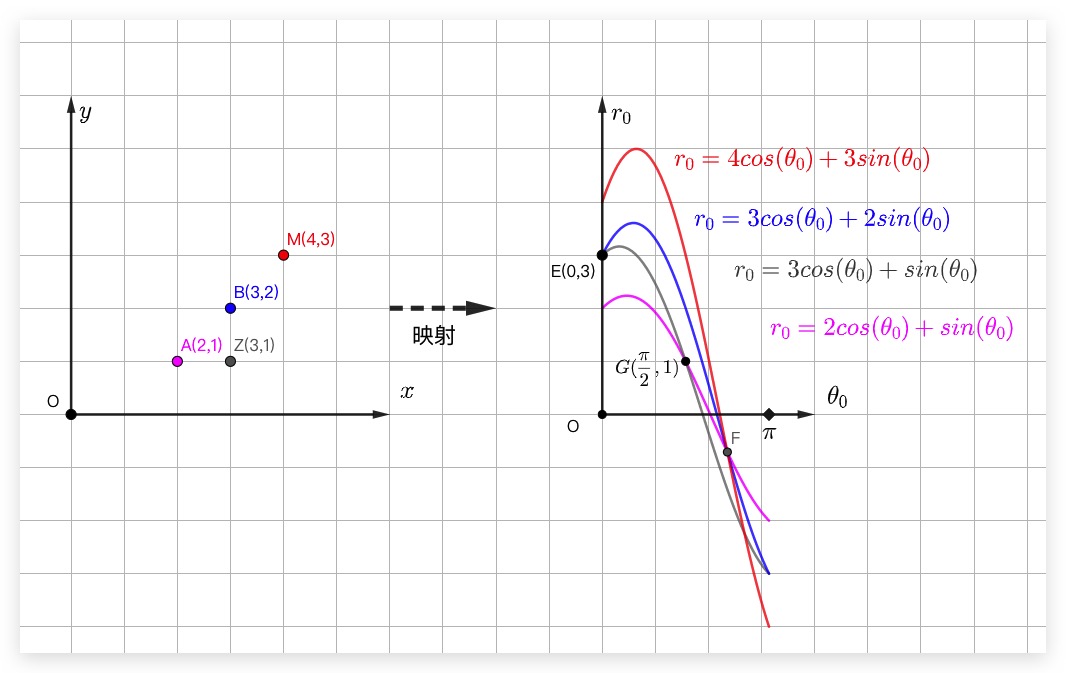
可以看到笛卡尔坐标系下的点A、B、M映射到极坐标系下的参数空间中实际上是线，而笛卡尔坐标系中的直线ABM映射到极坐标系下的参数空间中实际上是点F。即同样具备对偶性。且对于平行于X或Y轴的直线也可以很好映射到参数空间下，保证其有交点

直线检测

介绍完了Hough Transform之后，我们对于平面上的散点集中的直线检测就简单很多了。先通过极坐标系的参数空间将平面的散点集一一映射到其中，然后在参数空间中找出曲线相交较多的点，则其即为原散点集中被检测出的直线。故依据上图，我们可判定参数空间中的F点即为原散点集中被检测到的直线。通过Hough Transform，可以大大提高直线检测的效率

Note:

对于圆、椭圆等形状的检测，同样可以通过 Hough Transform 方法实现