排序算法(二): Merge Sort 归并排序

Merge Sort 归并排序，比较类排序算法中的一种。该算法运用了典型的分治思想，将大规模的元素排序问题分解为一个个的小规模级别排序，然后将这些小问题各个击破、分别排序，最后将各小规模级别问题的排序结果归并到一起，即完成整体排序

归并过程

在对一个数组归并排序时，需要先将其分为两半分别排序，然后将两部分的排序结果归并，即可得到一个原数组的排序结果。这里我们先对归并过程进行分析介绍并利用Java代码实现。下图即是一个将数组分为左、右两部分分别按升序排序后进行归并过程的图解

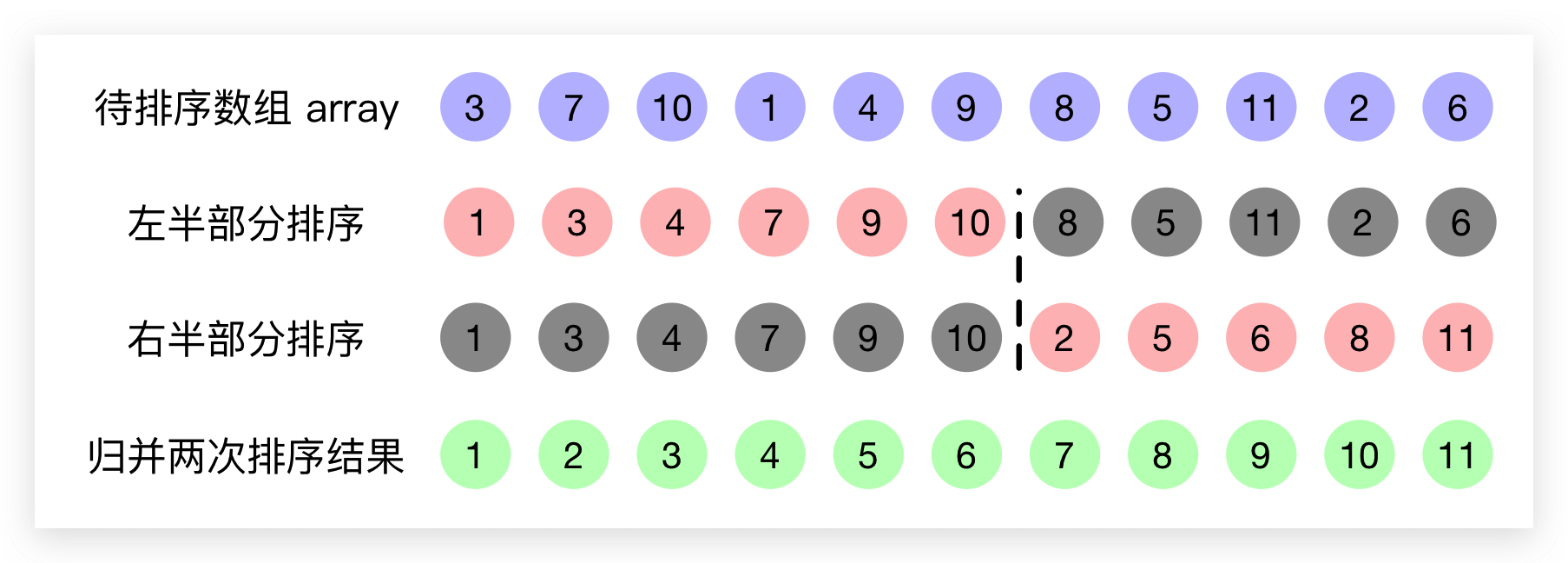
可以看到原待排序数组 array 在归并左、右两部分的排序结果过程前，需要先用一个单独的存储空间来保存其左、右两部分的排序结果再进行归并，故我们对含有N个元素的array数组进行排序前，先需要分配一个大小同样为N的辅助数组aux。归并时，先将array数组左、右两部分的排序结果拷贝到 aux 数组中；然后从 array数组左、右两部分的排序结果的副本aux数组中每次取最小(或最大)的元素放入array数组即完成归并

这里以Java为例实现了一个将数组array已按升序排列的左(array[start] ~ array[middle])、右(array[middle+1] ~ array[end])两部分归并在一起的归并函数merge()，这个归并函数merge() 我们在后面会多次看到它的应用场景

/**
 * 将两个升序的左半、右半数组(array[start]~array[middle]、array[middle+1]~array[end])归并为一个升序数组
 * @param array 待排序数组
 * @param start 起点
 * @param middle 中间点
 * @param end 终点
 */
private static void merge(int[] array, int start, int middle, int end) {
    // 先将 array[start]~array[end] 拷贝到辅助数组 aux[start]~aux[end] 中
    for(int k=start; k<=end; k++ ) {
        aux[k] = array[k];
    }

    int i = start;      // 左半升序数组(aux[start]~aux[middle])中 待归并元素的 位置索引
    int j = middle+1;   // 右半升序数组(aux[middle+1]~aux[end])中 待归并元素的 位置索引

    for(int k = start; k<=end; k++) {
        if( i>middle ) {     //  左半升序数组的元素已经归并完成，只能取右半升序数组中的元素
            array[k] = aux[j++];
        } else if( j>end ) { //  右半升序数组的元素已经归并完成，只能取左半升序数组中的元素
            array[k] = aux[i++];
        } else if( aux[i] <= aux[j] ) { // 左半升序数组的待归并元素aux[i] 不大于 右半升序数组的待归并元素aux[j]
            array[k] = aux[i++];
        } else {
            array[k] = aux[j++];
        }
    }
}

实现分治

前文说到归并排序是分治思想的经典实例，那么我们如何在归并排序中具体实践这一思想呢？这里将告诉大家，我们可以通过两种更具体的手段实现分治——自底向上的迭代、自顶向下的递归，现在我们分别就两种方法细细道来

自底向上的迭代

算法思想

很多朋友看到上文的归并图解时，一定有个疑问，归并时，需要数组的左、右半两部分已经是有序状态，然后才能对其归并，那如何保证对数组的左、右两半部分进行排序呢？其实，答案很简单，当左、右两半部分的个数分别只有1时，即已是有序状态，此时即可通过归并操作，获得有序的大小为2的子数组；然后再对两个有序的大小为2的数组进行归并操作，即可获得有序的大小为4的子数组。不断重复上述过程，即可完成整个数组的排序工作

算法图解

这里以对 N 个元素的数组 array 进行升序排列为例，给出归并排序过程的图解

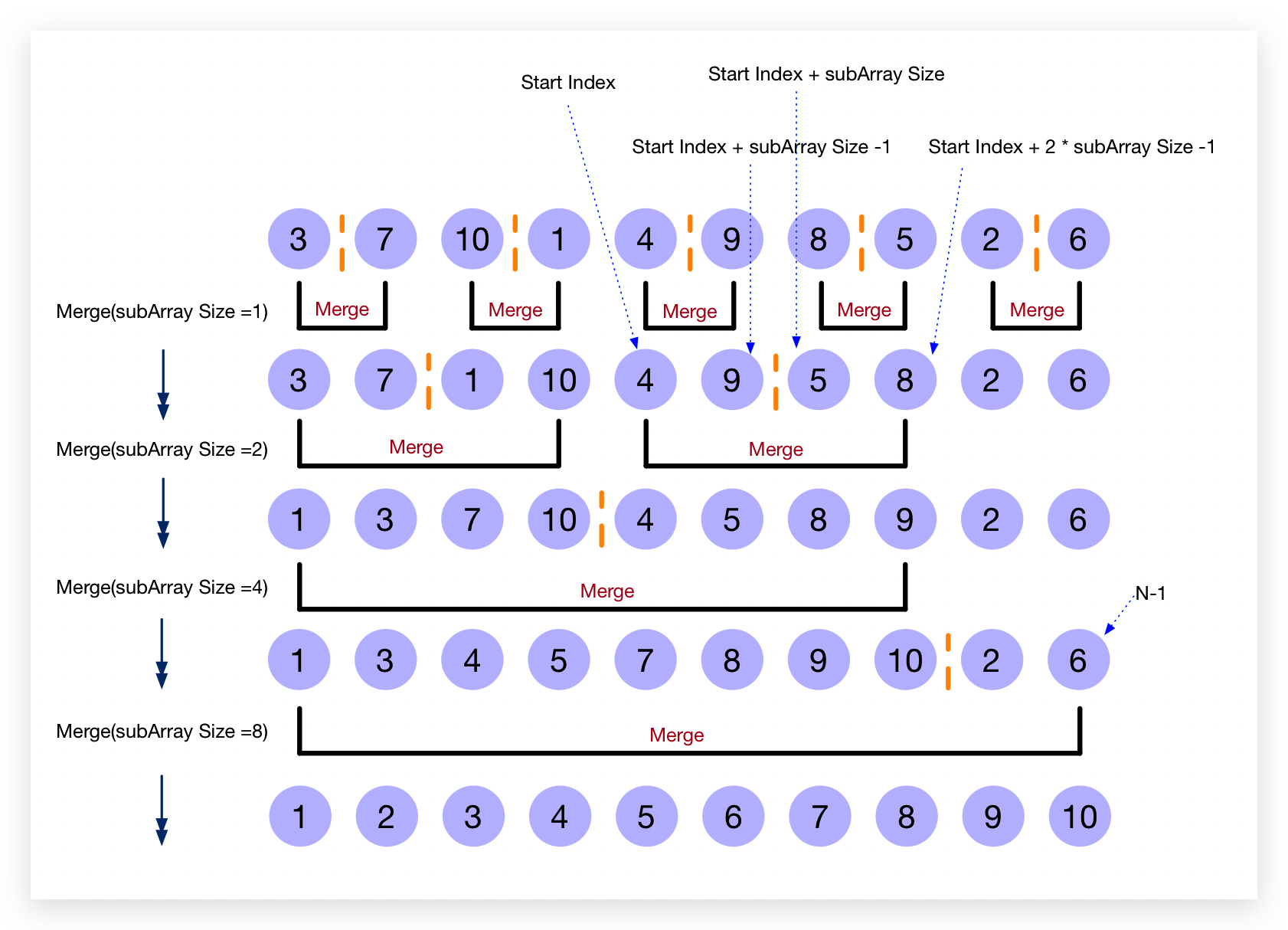
Java 代码示例

现通过Java代码实现上述基于迭代的自底向上的归并排序(merge方法实现在上文已给出，此处不再赘述)。下述代码的外循环，我们改变的是在每轮归并过程中一分为二后的半部分数组subArray的大小，易知，其大小从1开始，每轮归并结束开启下一轮归并时，其subArray大小正好翻倍。在每次归并时，我们需要同时给定两个半部分数组subArray，即满足条件: Start Index + subArray Size <= N-1，由于上式中参数均为整数，故可化简: Start Index < N - subArray Size。一般情况下，每次归并时，左、右两个半部分数组subArray的大小是一样的，但是在每轮归并的最后一次归并时，右半部分数组的元素可能会不足subArray Size。所以下述代码merge函数中的形参end应取 start+2*subArraySize-1 与 N-1 的最小值

/**
 * 归并排序
 */
public class MergeSort {

    /**
     * 用于归并排序的辅助数组
     */
    private static int[] aux;
    
    /**
     * 升序排列(通过迭代实现)
     */
    public static void sort2() {
        int[] array = getTestCase();
        int size = array.length;

        System.out.println("before sort: " + Arrays.toString(array) );

        aux = new int[size];    // 分配辅助数组空间
        for( int subArraySize = 1; subArraySize<size; subArraySize *= 2) {
            for( int start = 0; start<size-subArraySize; start += 2*subArraySize ) {
                merge( array, start, start+subArraySize-1, Math.min(start+2*subArraySize-1, size-1) );
            }
        }

        System.out.println("after sort: " + Arrays.toString(array) );
    }
   
    /**
     * 获取测试用例
     */
    private static int[] getTestCase() {
        int[] caseArray = {3,7,10,1,4,9,8,5,2,6};
        return caseArray;
    }
}

测试结果:

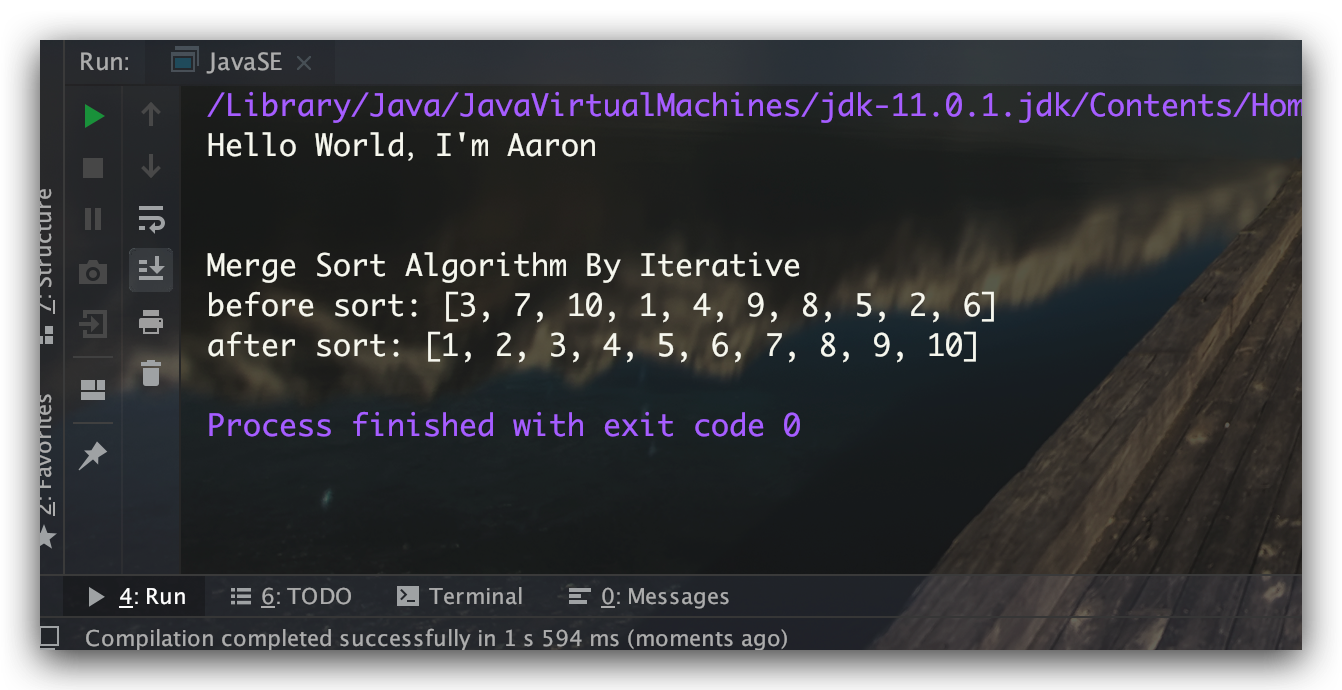
自顶向下的递归

算法思想

上文我们介绍了如何通过迭代实现分治，这里介绍如何使用递归实现归并排序的分治。其实也很简单，就是先对欲排序数组的左半部分排序，再对欲排序数据的右半部分排序，最后将左、右两半部分归并到一起。对上述过程不断递归，即可完成对整个数组的排序

算法图解

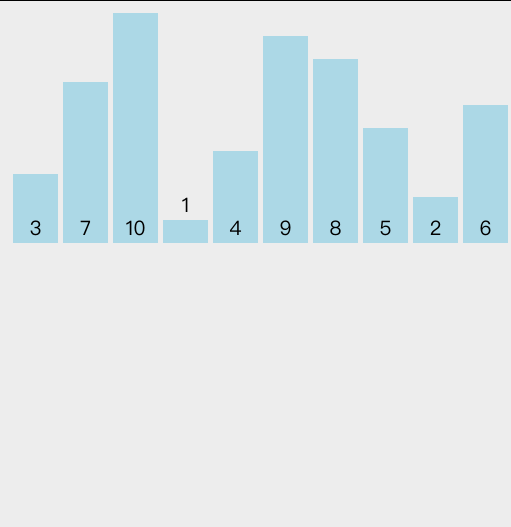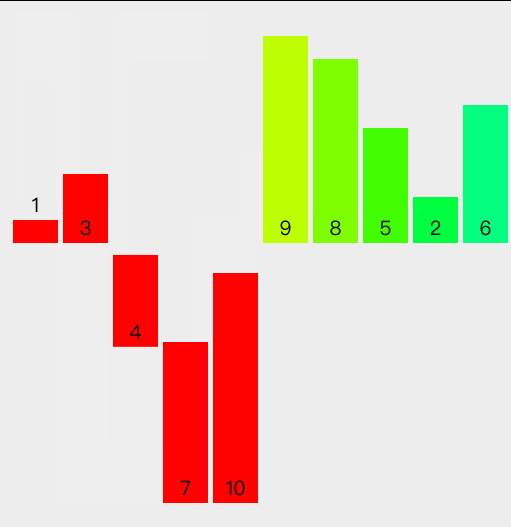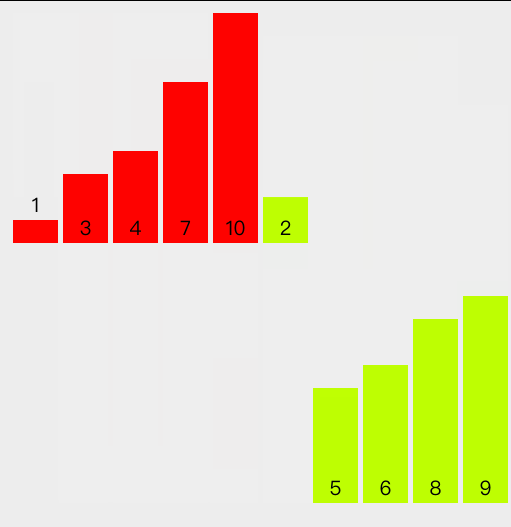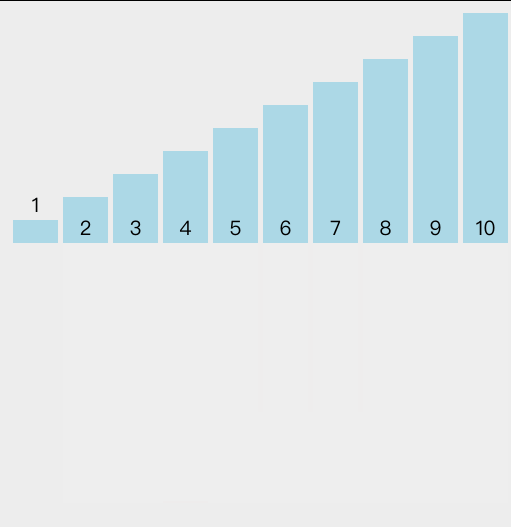
Java 代码示例

现通过Java代码实现上述基于递归的自顶向下的归并排序(merge方法实现在上文已给出，此处不再赘述)。值得一提的是，计算数组中间点索引时，建议通过 start + (end - start) / 2 而不是(start+end)/2 计算，以避免因start、end过大而可能发生的溢出

/**
 * 归并排序
 */
public class MergeSort {

    /**
     * 用于归并排序的辅助数组
     */
    private static int[] aux;

    /**
     * 升序排列(通过递归实现)
     */
    public static void sort1() {
        int[] array = getTestCase();
        int size = array.length;

        System.out.println("before sort: " + Arrays.toString(array) );

        aux = new int[size];    // 分配辅助数组空间
        sort(array, 0, size-1); // 归并排序

        System.out.println("after sort: " + Arrays.toString(array) );
    }

    /**
     * 对数组指定范围的元素进行升序排列
     * @param array 待排序数组
     * @param start 起点
     * @param end 终点
     */
    private static void sort(int[] array, int start, int end) {
        if( start >= end ) {
            return;
        }
        int middle = start + (end - start) / 2;
        sort(array, start, middle);   // 先对数组左半部分进行排序
        sort(array, middle+1, end);   // 再对数组右半部分进行排序
        merge(array, start, middle, end);  // 最后将两个升序的左半、右半数组归并为一个升序数组
    }
    /**
     * 获取测试用例
     */
    private static int[] getTestCase() {
        int[] caseArray = {3,7,10,1,4,9,8,5,2,6};
        return caseArray;
    }
}

测试结果:

特点

时间复杂度(average)	时间复杂度(worst)	时间复杂度(best)	空间复杂度	稳定性
$O(N \log N)$	$O(N \log N)$	$O(N \log N)$	$O(N)$	稳定

参考文献

算法(第4版) Robert Sedgewick、Kevin Wayne 著